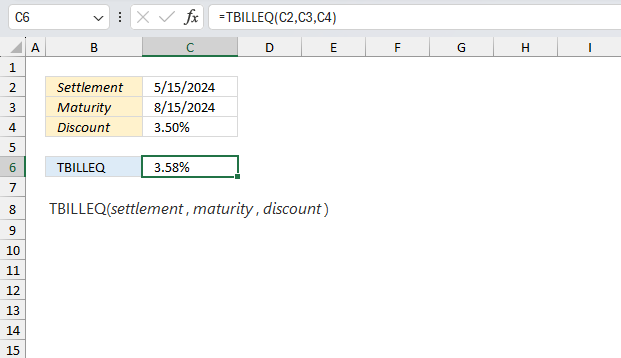
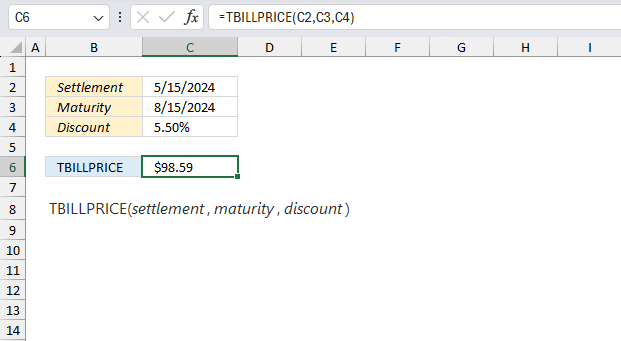
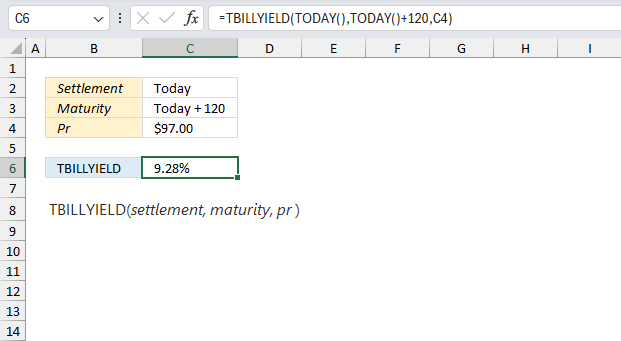
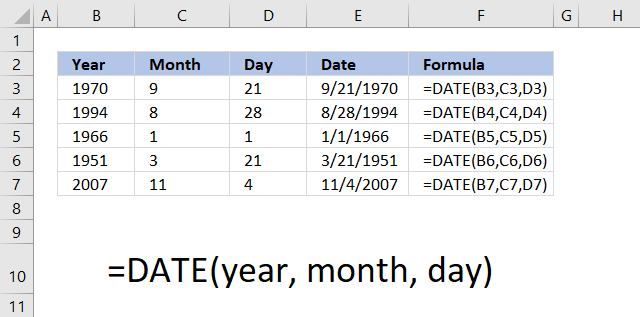Excel Functions by category
Functions alphabetically | Functions by category
Functions are sorted by category, click a category name to find Excel functions in that category.
Array manipulation
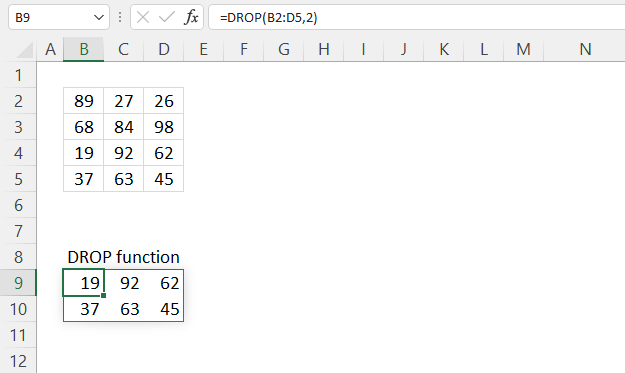
DROP function removes a given number of rows or columns from a 2D cell range or array.
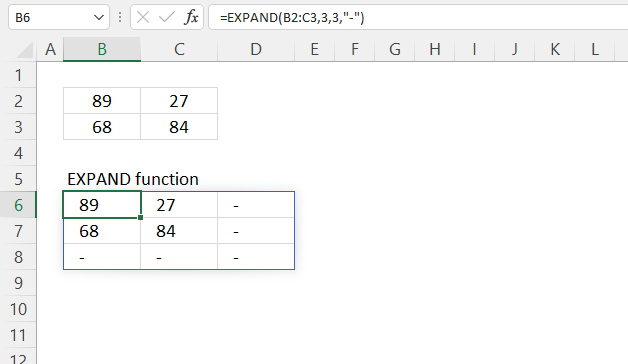
EXPAND function increases a cell range or array by a specified number of columns and rows.
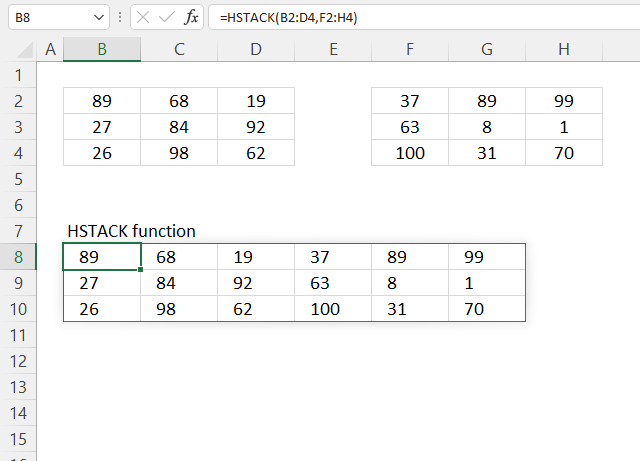
HSTACK function combines cell ranges or arrays. Joins data to the first blank cell to the right of a cell range or array (horizontal stacking)
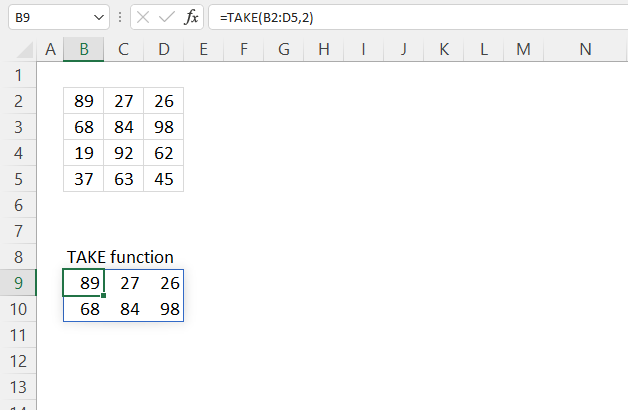
TAKE function returns a given number of rows or columns from a 2D cell range or array.
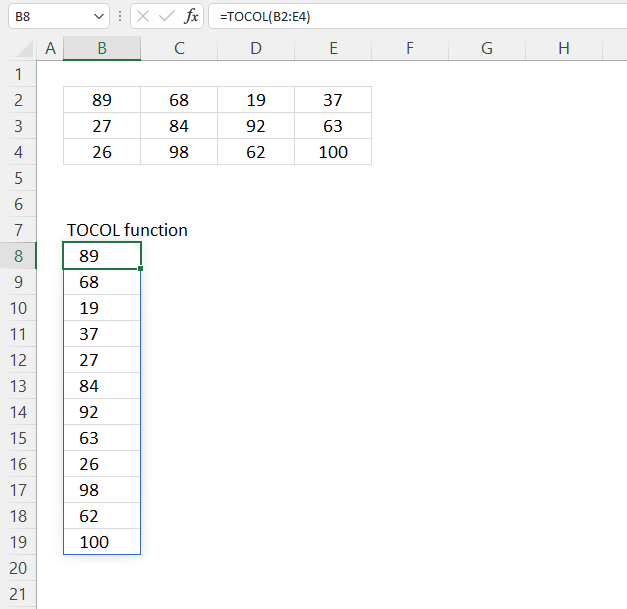
TOCOL function rearranges values in 2D cell ranges to a single column.
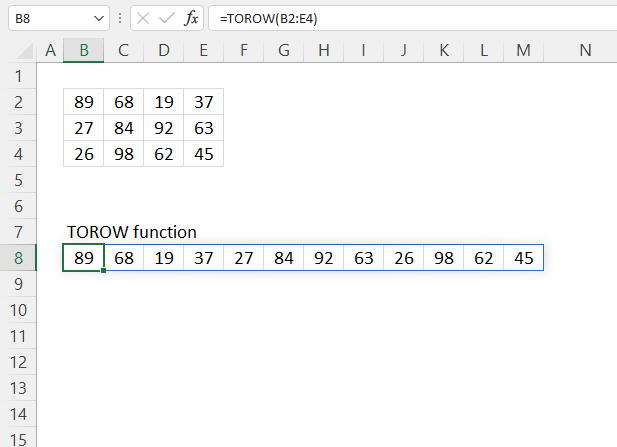
TOROW function rearranges values from a 2D cell range to a single row.
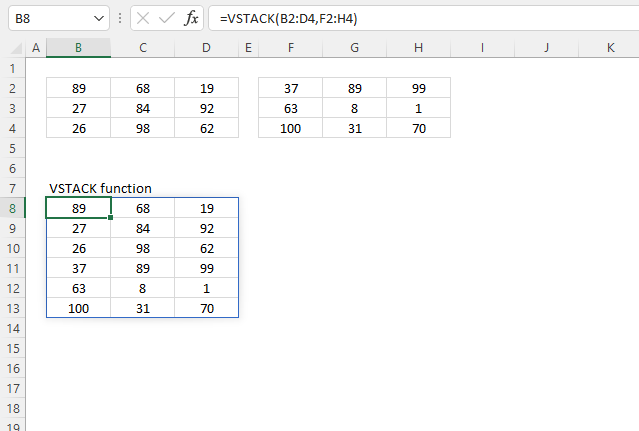
VSTACK function combines cell ranges or arrays. Joins data to the first blank cell at the bottom of a cell range or array (vertical stacking)
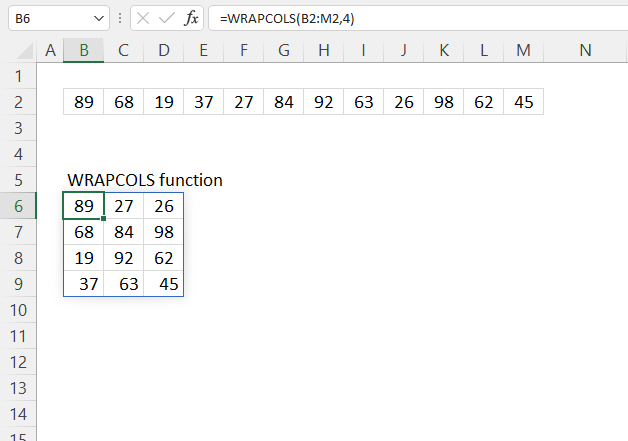
WRAPCOLS function rearranges values from a single row to a 2D cell range based on a given number of values per column.
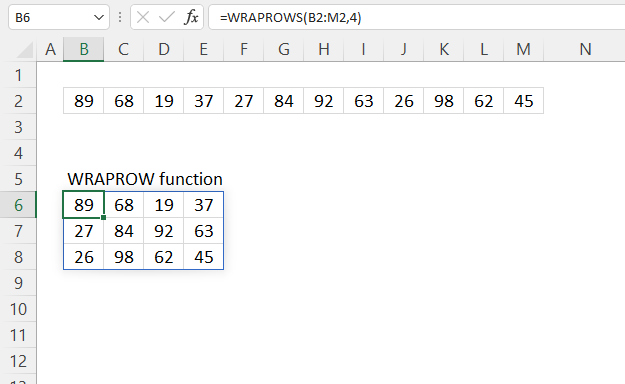
WRAPROWS function rearranges values from a single row to a 2D cell range based on a given number of values per column.
Back to top
Compatibility
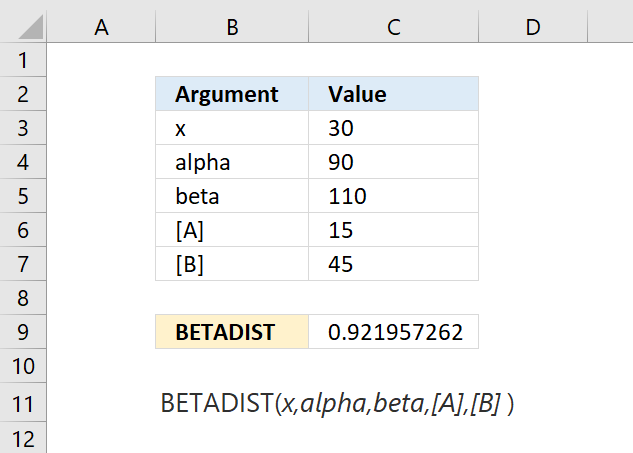
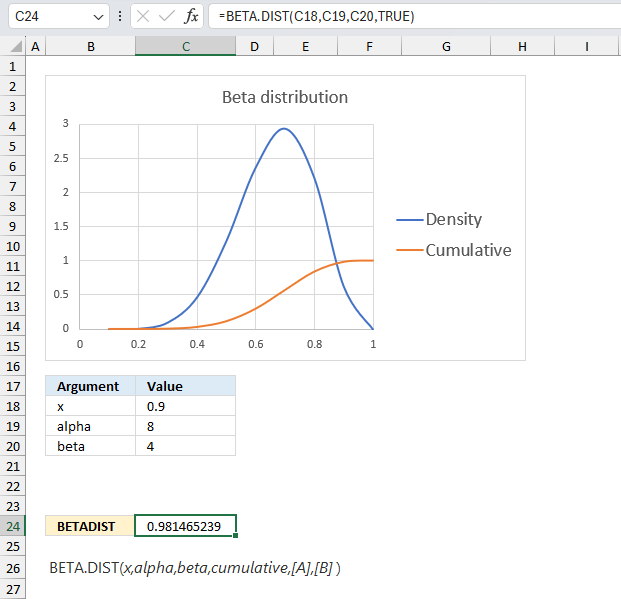
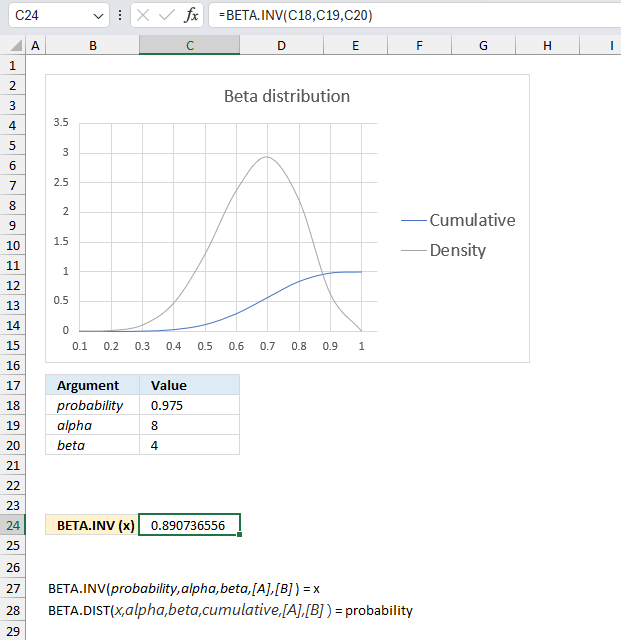
BETADIST function calculates the beta distribution, it represents outcomes in the form of probabilities.
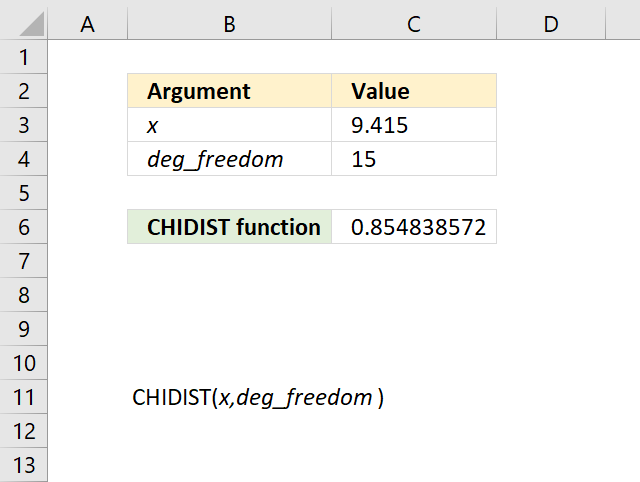
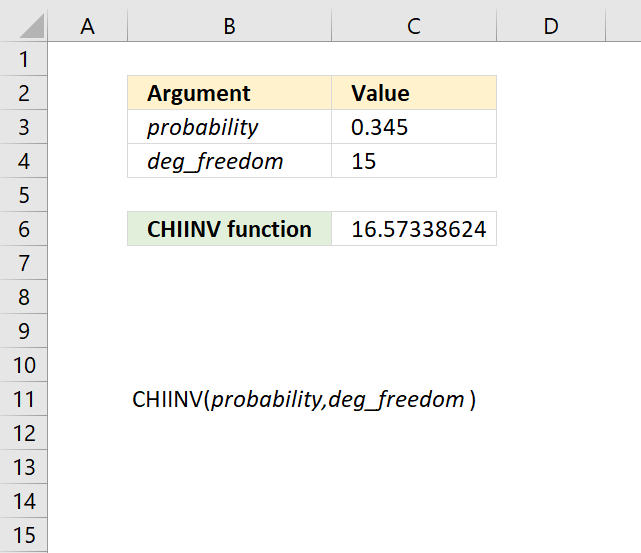
CHIINV function calculates the inverse probability of the chi-squared distribution.
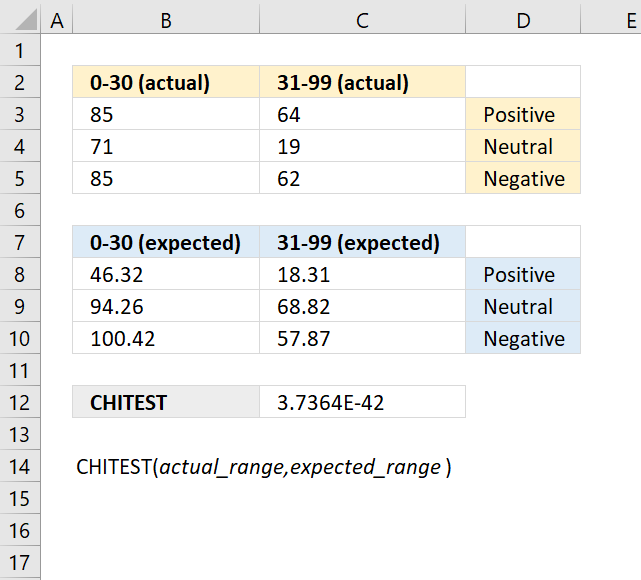
CHITEST function calculates the test for independence, the value returned from the chi-squared statistical distribution and the correct degrees of freedom. Use this function to check if hypothesized results are valid.
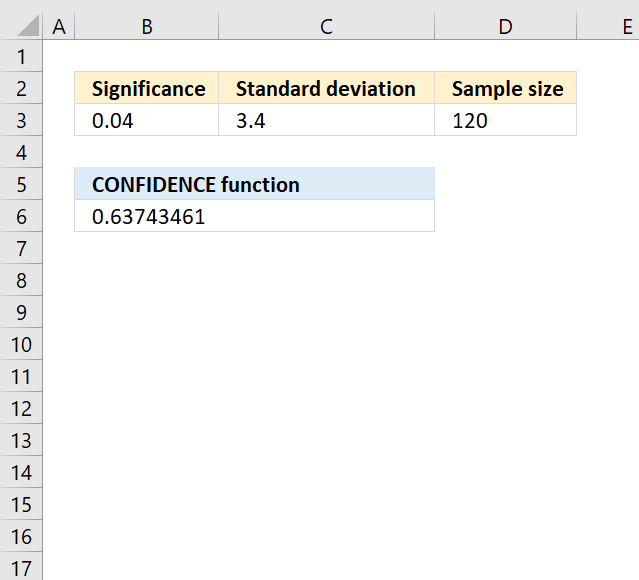
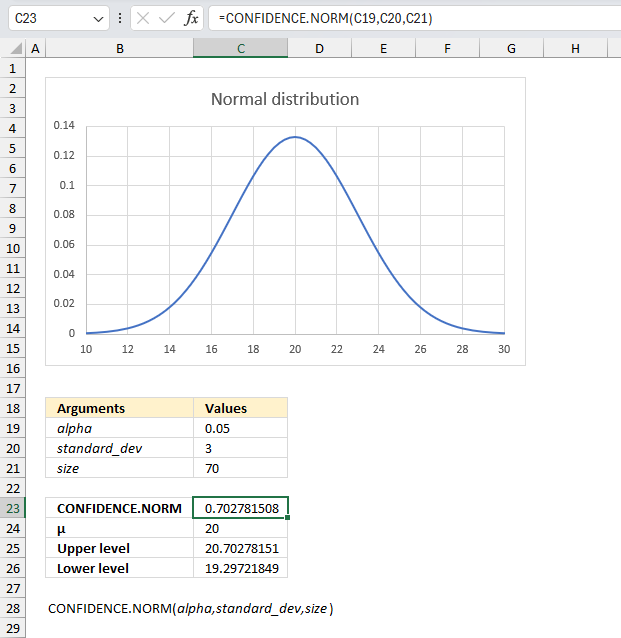
CONFIDENCE function calculates the confidence interval for a population mean, using a normal distribution.
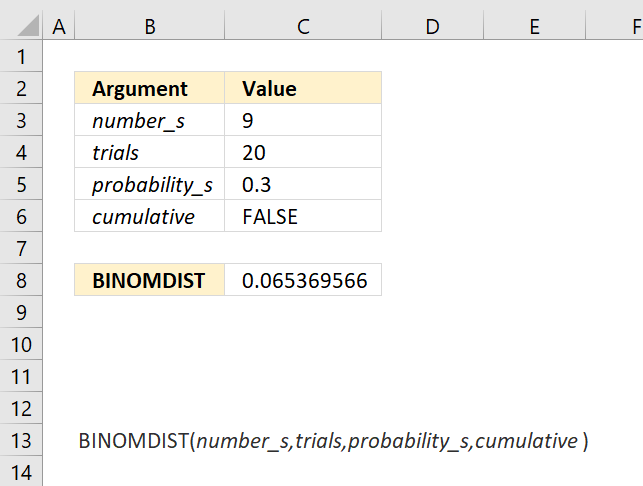
CRITBINOM function calculates the minimum value for which the binomial distribution is equal to or greater than a given threshold value.
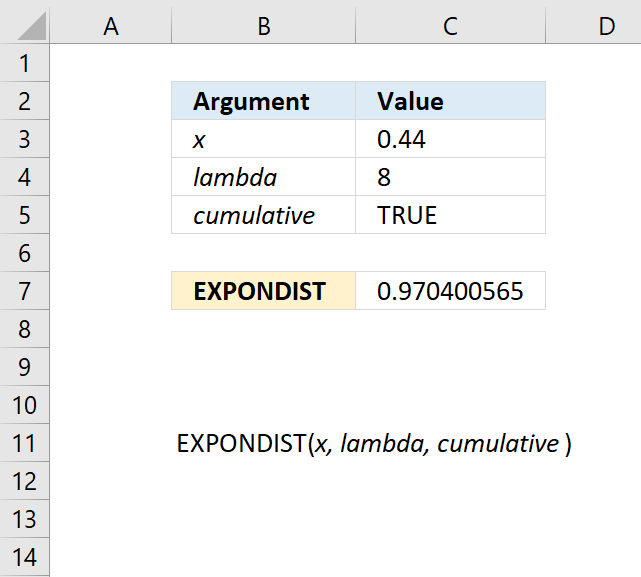
EXPONDIST function calculates the exponential distribution representing an outcome in the form of probability.
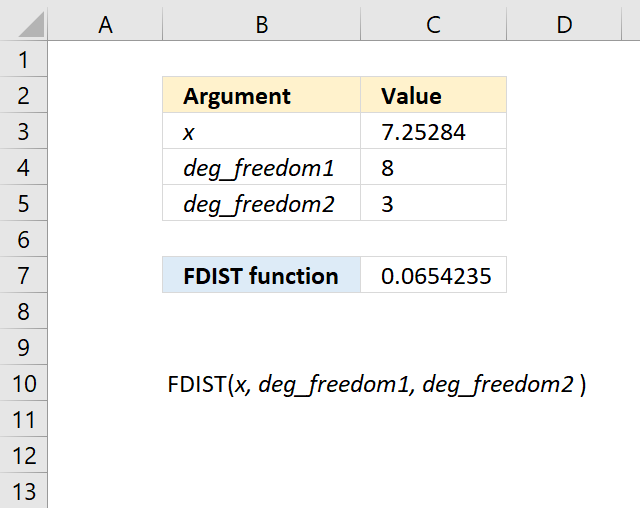
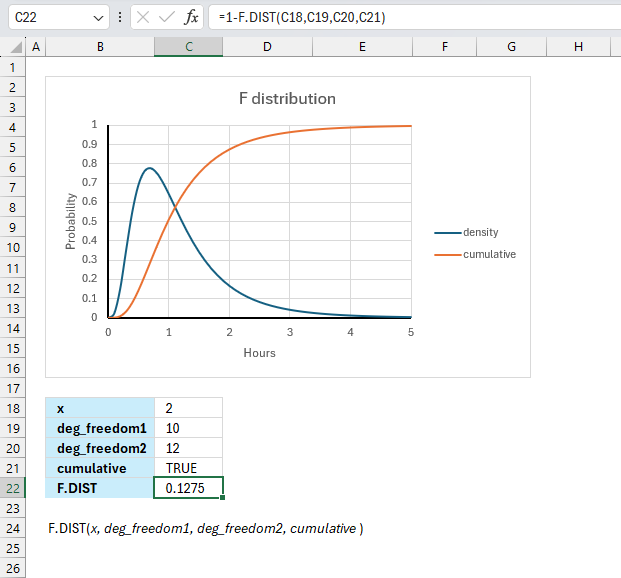
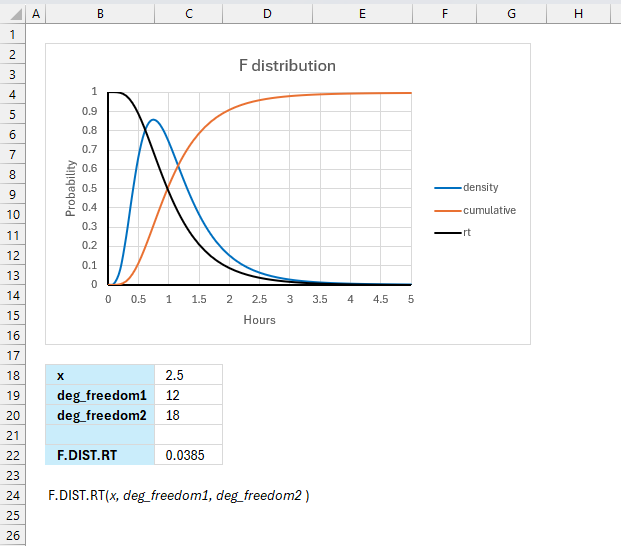
FDIST function calculates the F probability of the right-tailed distribution for two tests.
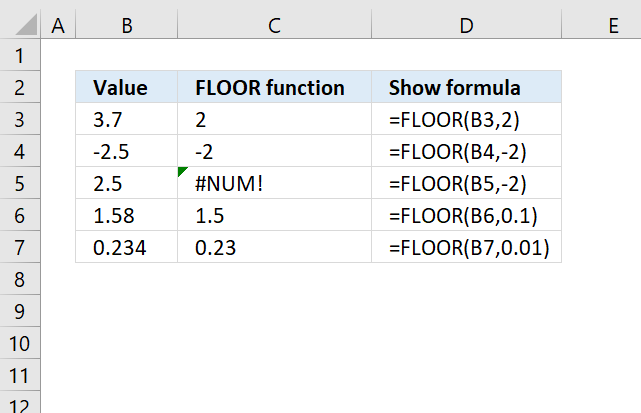
FLOOR function rounds a number down, toward zero, to the nearest multiple of significance.
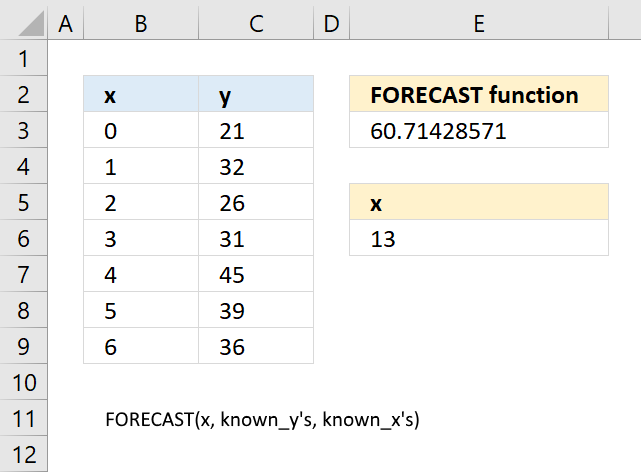
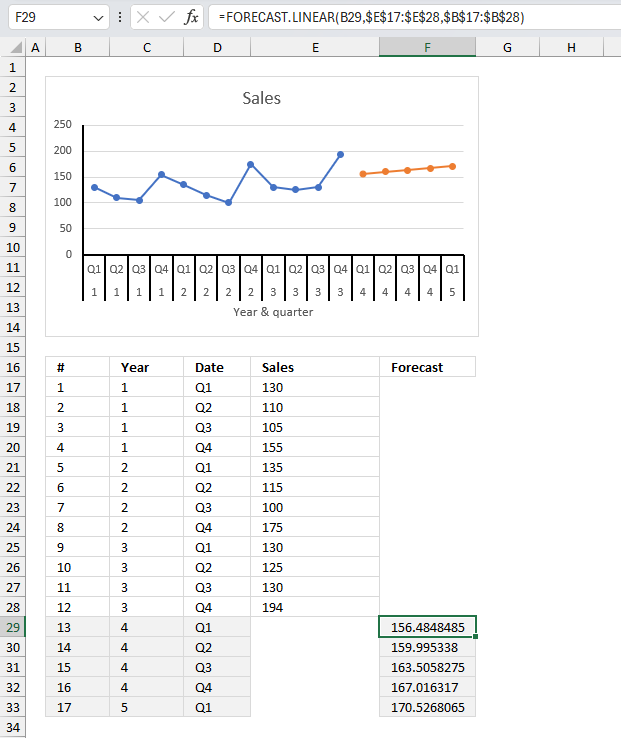
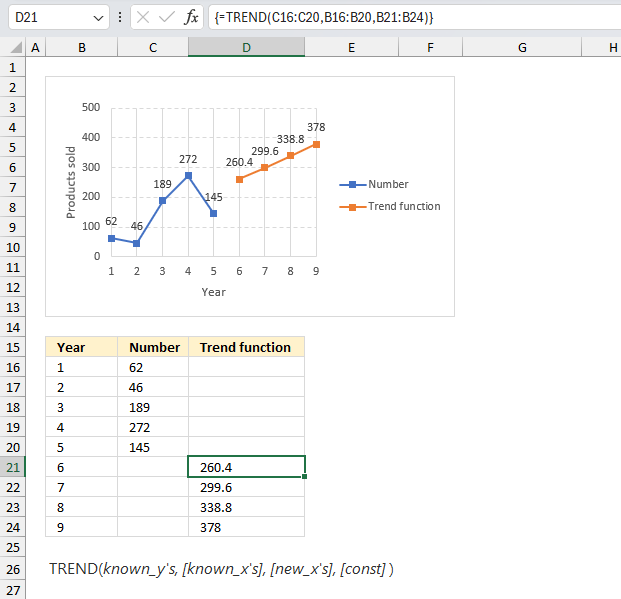
FORECAST function calculates a value based on existing x and y values using linear regression. Use this function to predict linear trends.
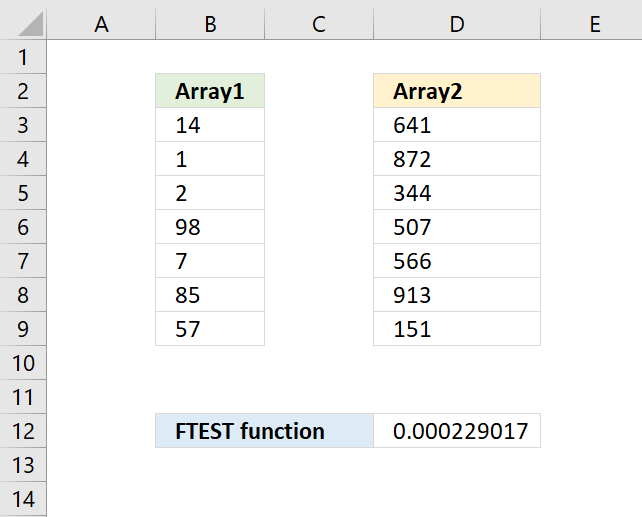
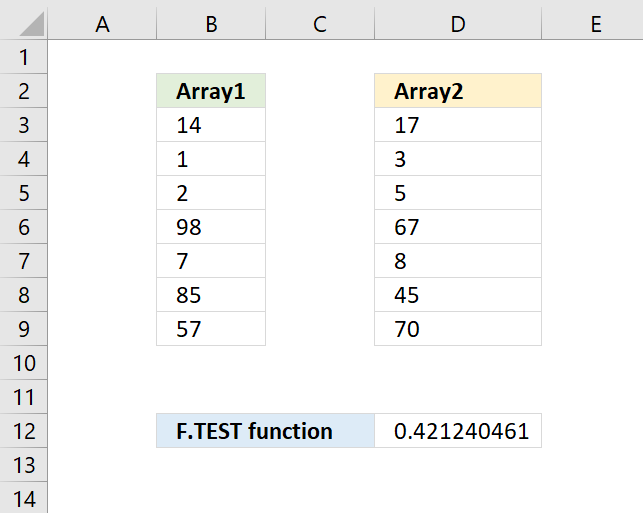
FTEST function calculates the value from an F-test. The value shows if the variances from two data sets are not significantly different.
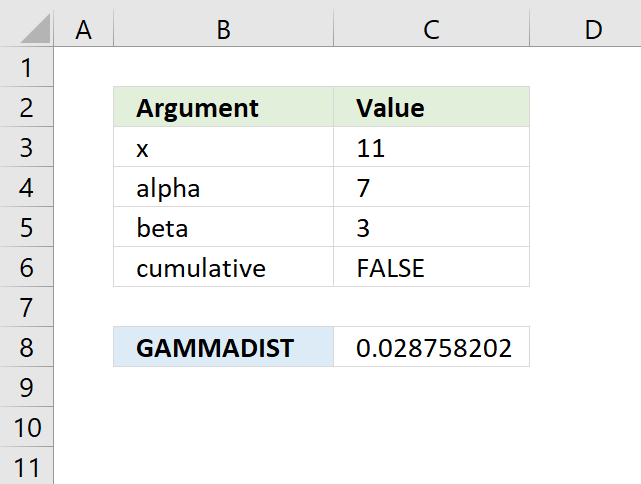
GAMMADIST function calculates the gamma often used in queuing analysis (probability statistics).
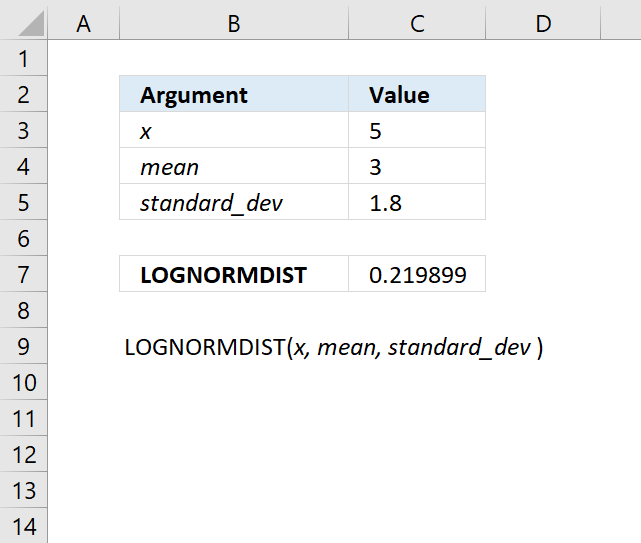
LOGNORMDIST function calculates the cumulative lognormal distribution of argument x, based on a normally distributed ln(x) with the arguments of mean and standard_dev.
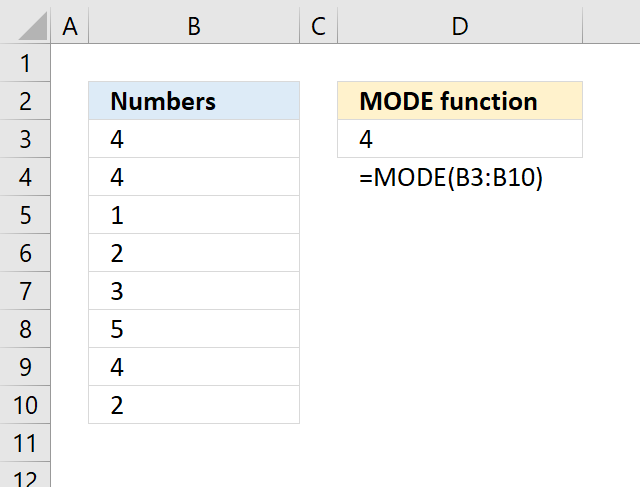
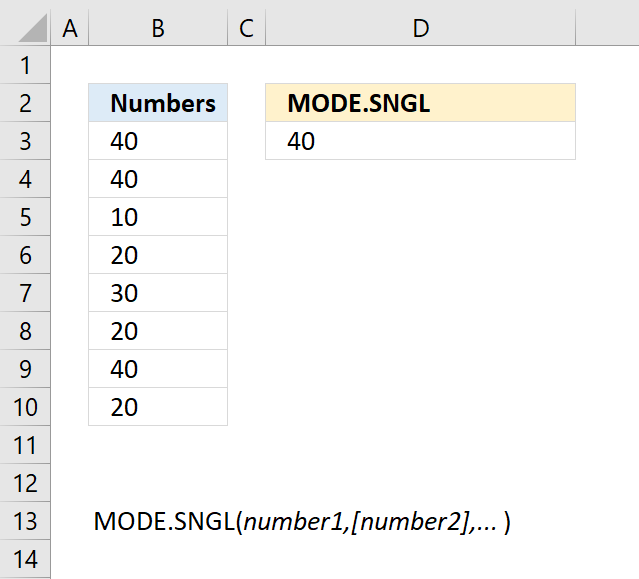
MODE function calculates the most frequent number in a cell range.
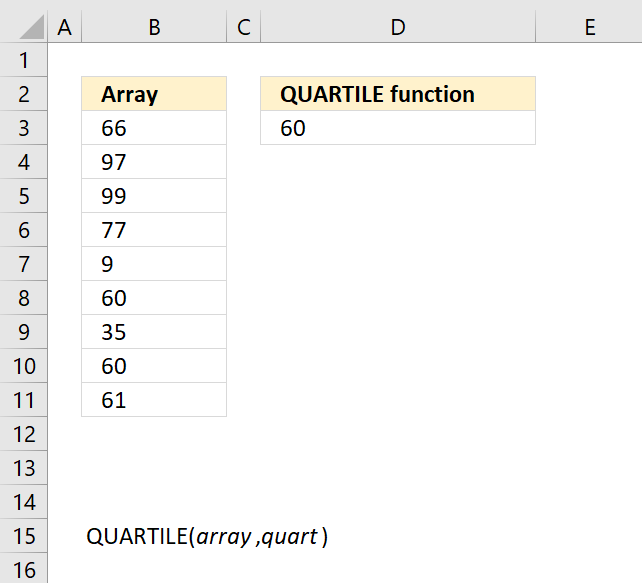
QUARTILE function returns the quartile of a data set, use the QUARTILE function to divide data into groups.
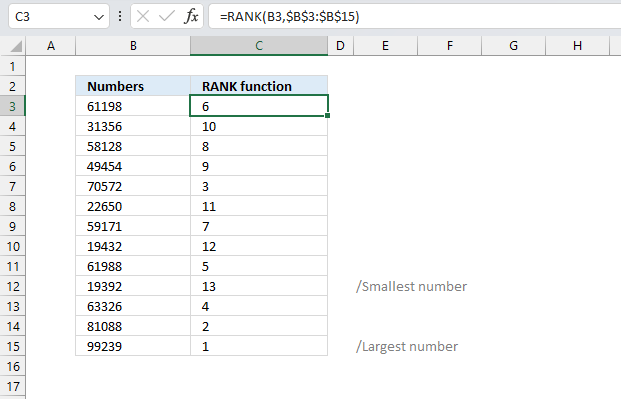
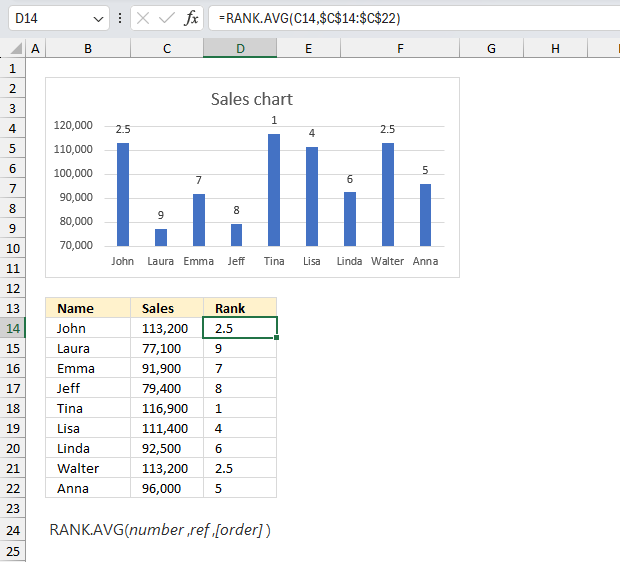
RANK function calculates the rank of a specific number compared to a list of numbers.
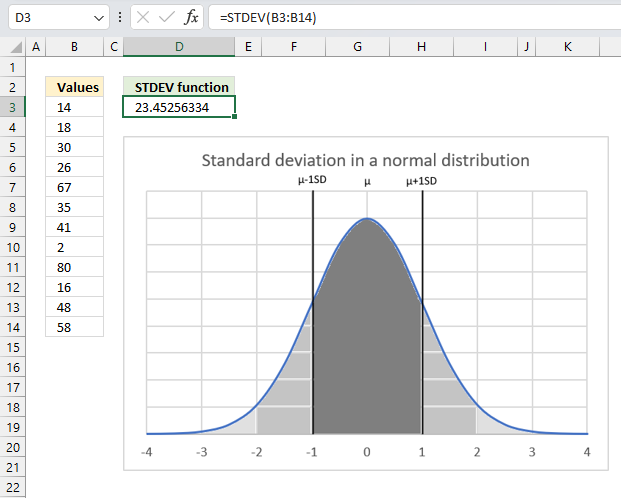
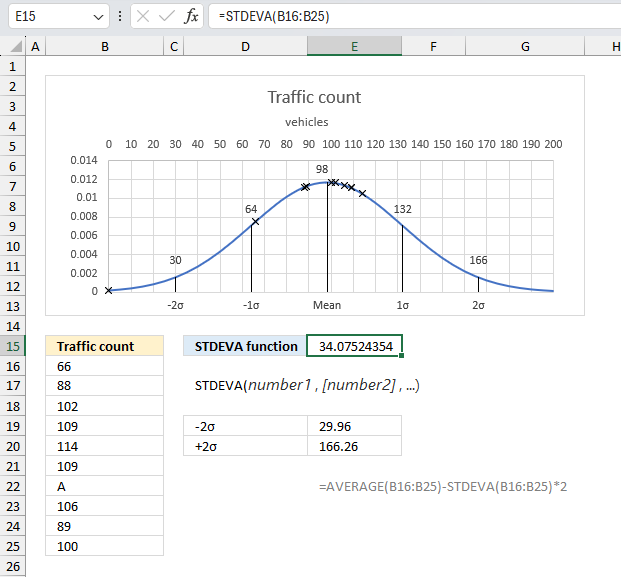
STDEV function calculates the standard deviation of a group of values.
Back to top
Database
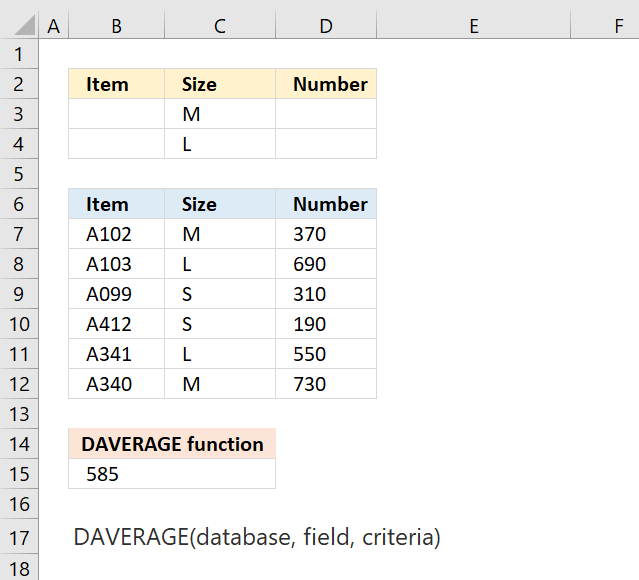
DAVERAGE function calculates an average based on values in a list or database that meet specific conditions.
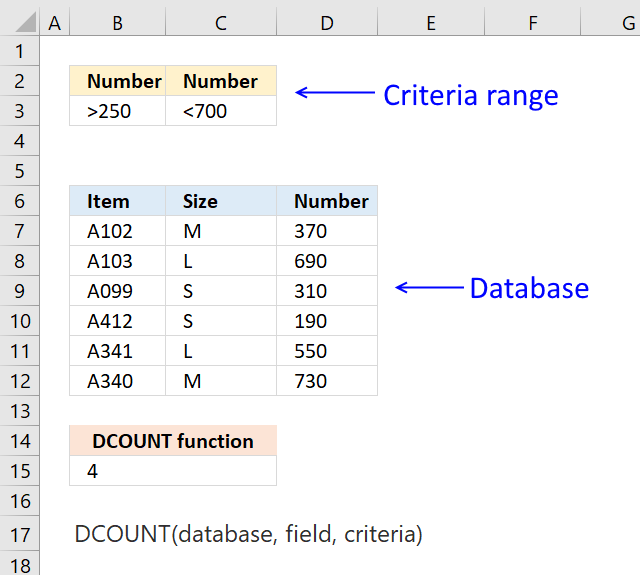
DCOUNT function counts cells containing numbers and that meet a condition or criteria.
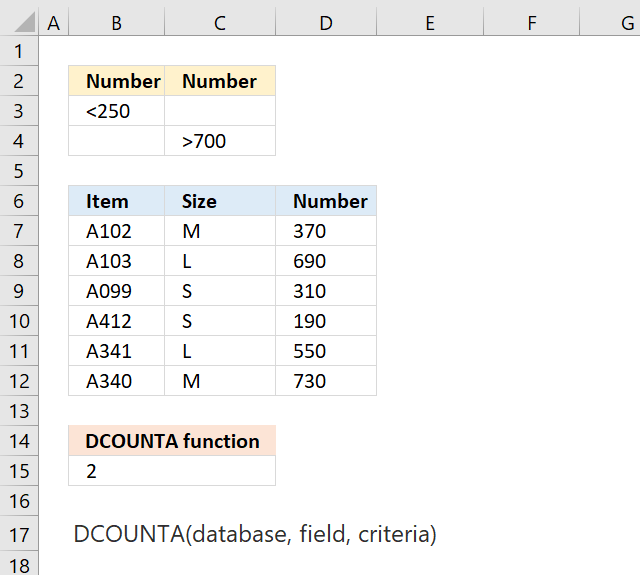
DCOUNTA function counts nonempty cells in a column you specify, in a database where records also meet a condition or criteria.
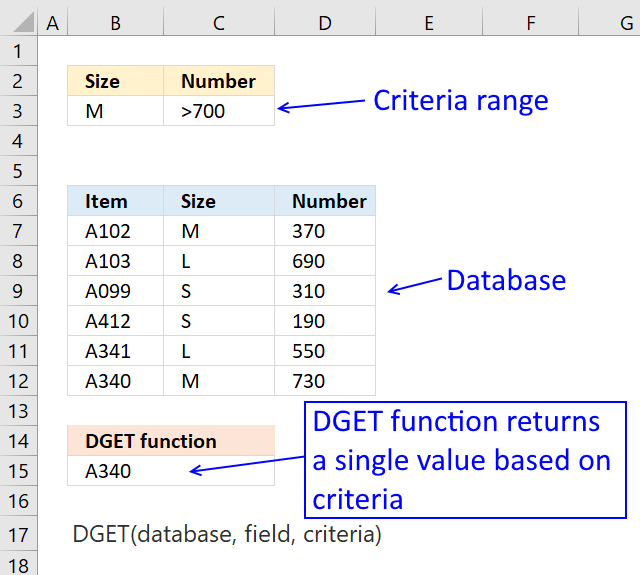
DGET function fetches a value from a column in a database whose records meet a condition or criteria.
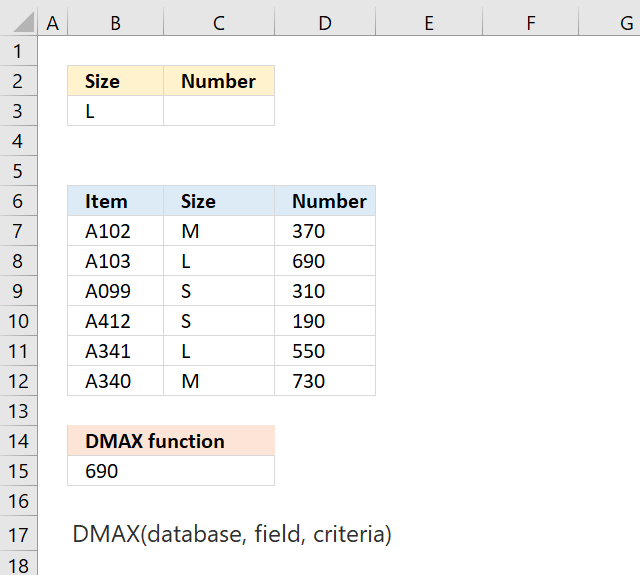
DMAX function extracts the maximum number from a column in a database whose records match a condition or criteria.
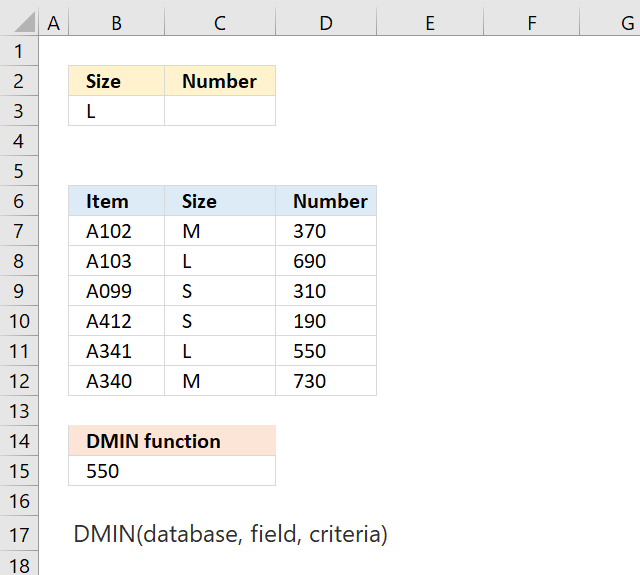
DMIN function extracts the smallest number from a column in a database whose records match a condition or criteria.
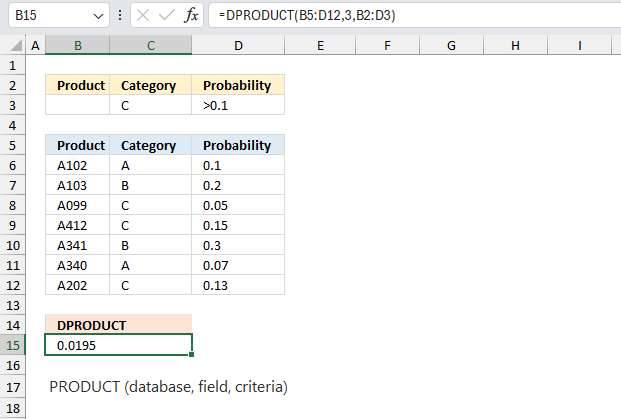
DPRODUCT function multiplies numbers that match a condition or criteria in a database.
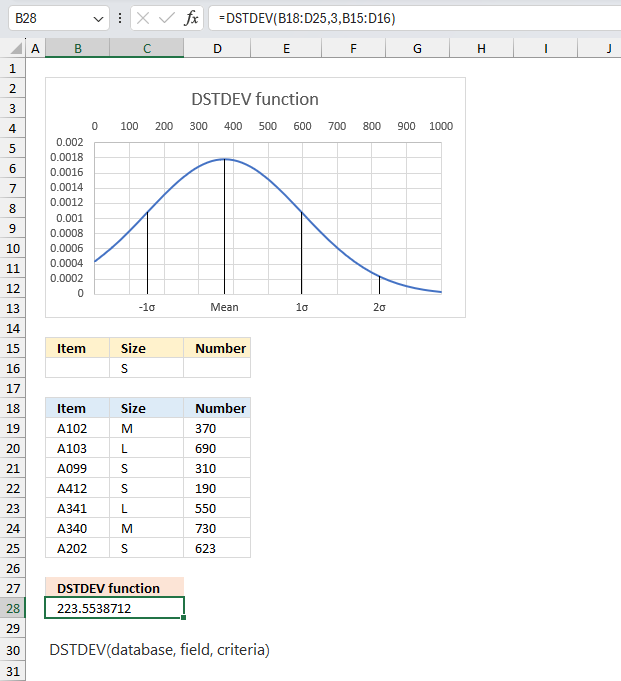
DSTDEV function calculates an estimation of the standard deviation based on a sample of a population. The function also allows you to specify criteria applied to a database.
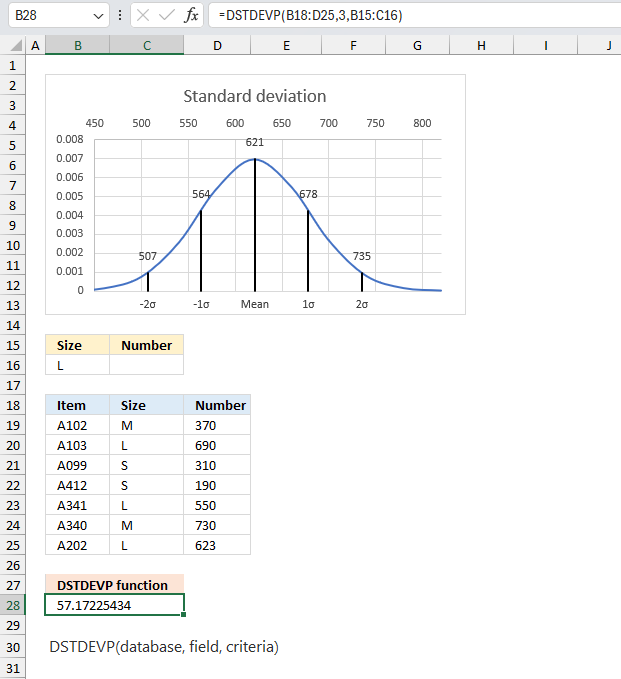
DSTDEVP function calculates the standard deviation based on a population. The function also allows you to specify criteria applied to a database.
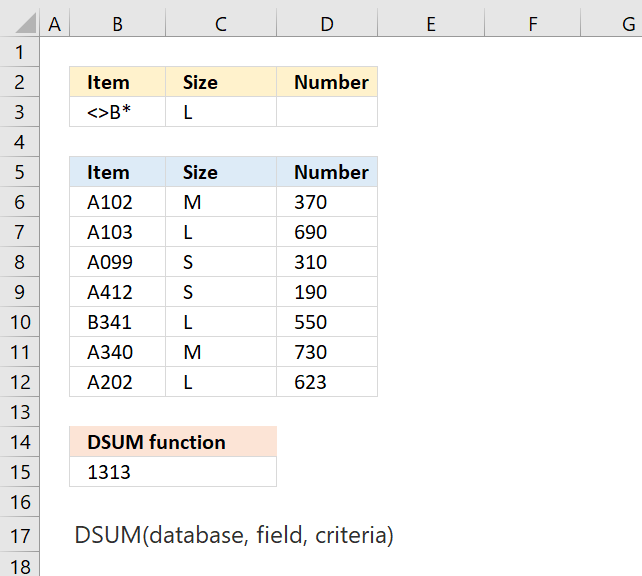
DSUM function adds numbers in a database/list that meets a condition or criteria.
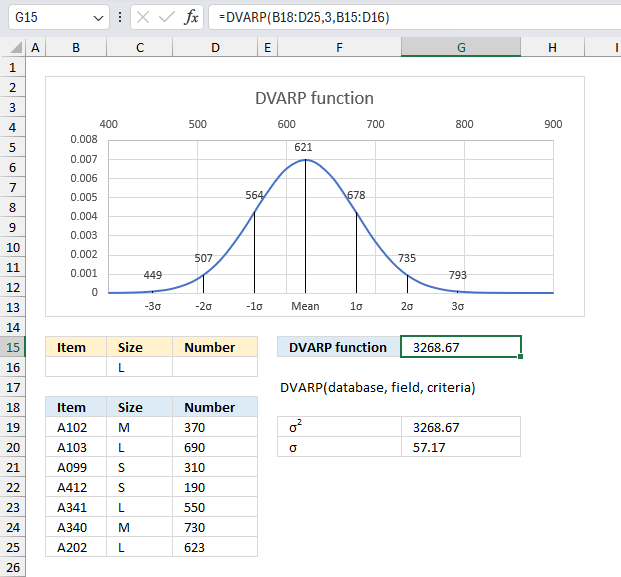
DVARP function returns the variance of an entire population. The numbers are in a column of records in a dataset or database that meets a given condition or criteria.
Back to top
Date and Time
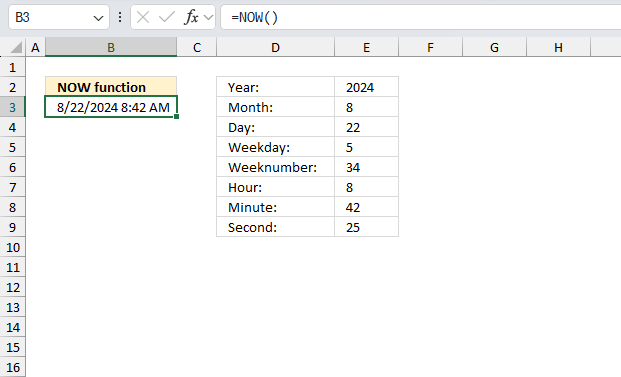
DATE function returns a number that acts as a date in the Excel environment.
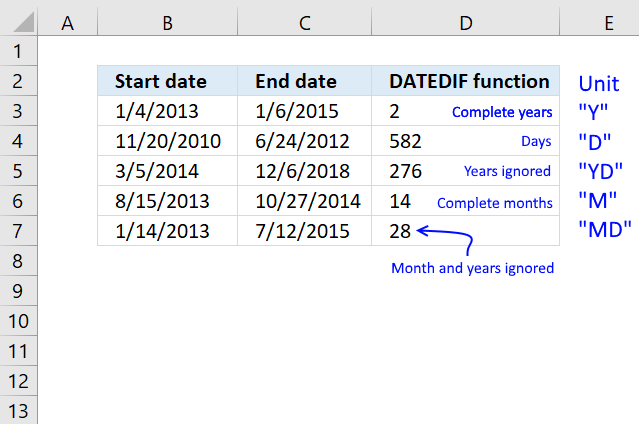
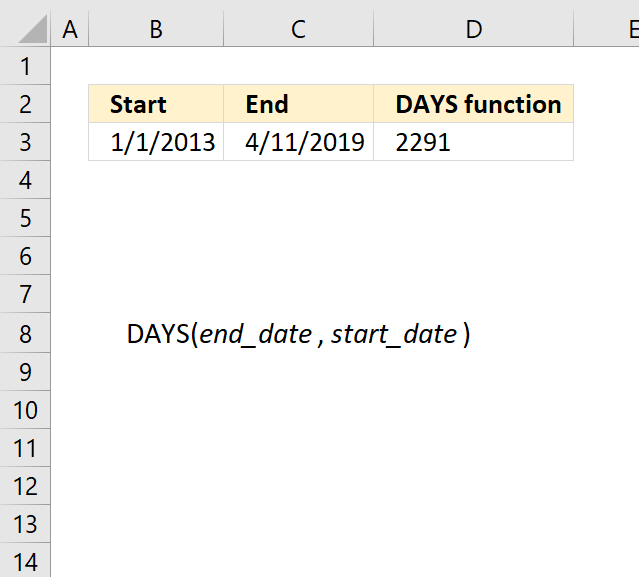
DATEDIF function returns the number of days, months, or years between two dates. The DATEDIF function exists in order to ensure compatibility with Louts 1-2-3.
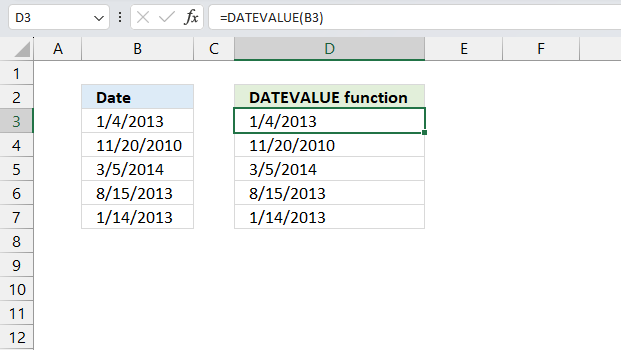
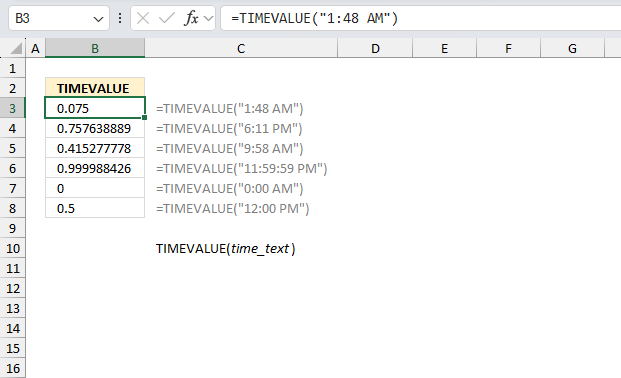
DATEVALUE function returns an Excel date value (serial number) based on a date stored as text.
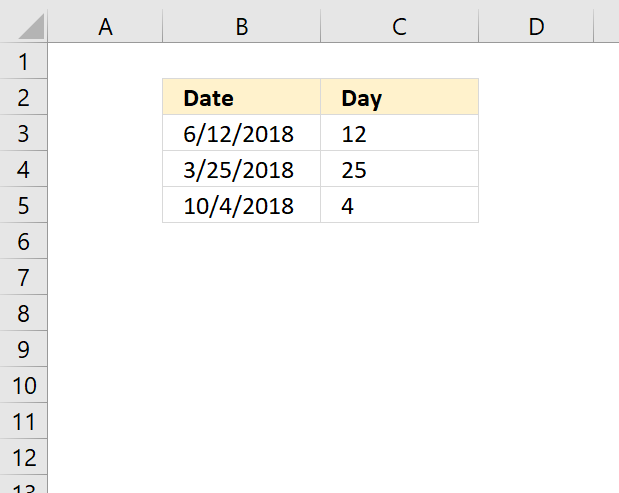
DAY function extracts the day as a number from an Excel date.
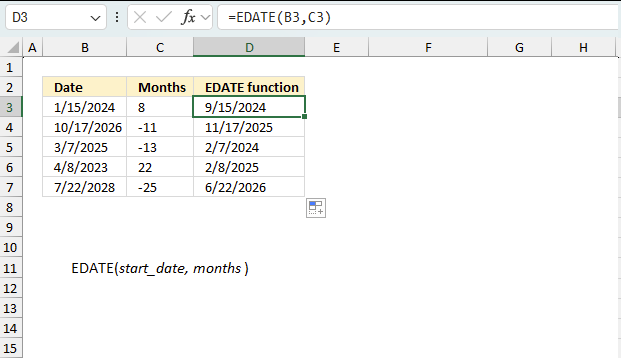
EDATE function returns a date determined by a start date and a number representing how many months.
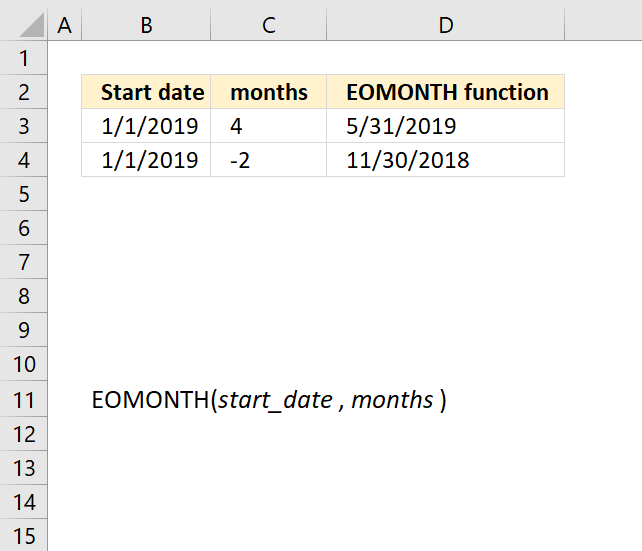
EOMONTH function returns an Excel date for the last day of a given month using a number and a start date.
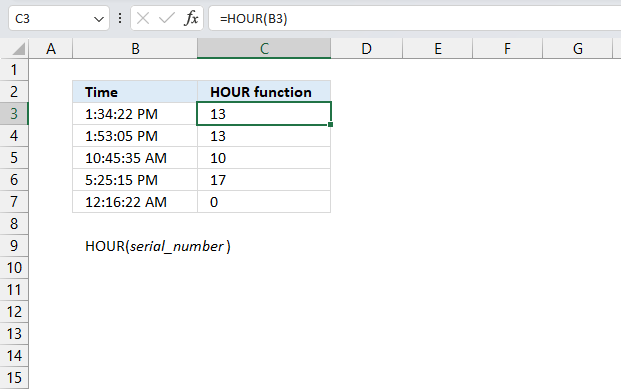
HOUR function returns an integer representing the hour of an Excel time value.
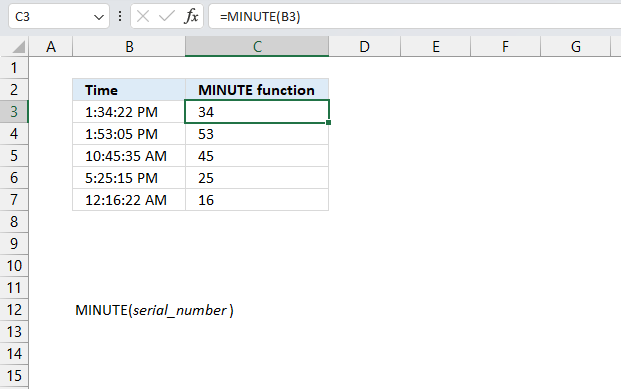
MINUTE function returns a whole number representing the minute based on an Excel time value. The returned number is ranging from 0 to 59.
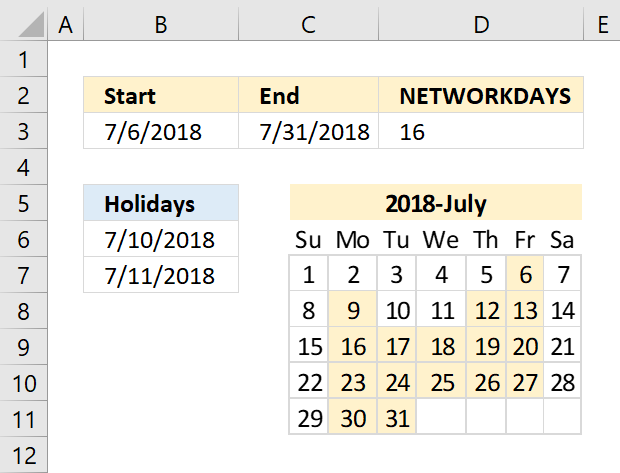
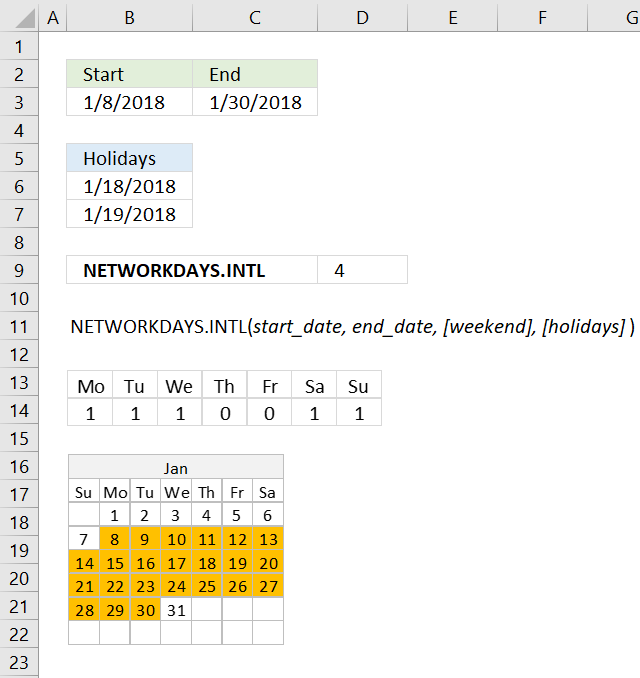
NETWORKDAYS function returns the number of working days between two dates, excluding weekends. It also allows you to ignore a list of holiday dates that you can specify.
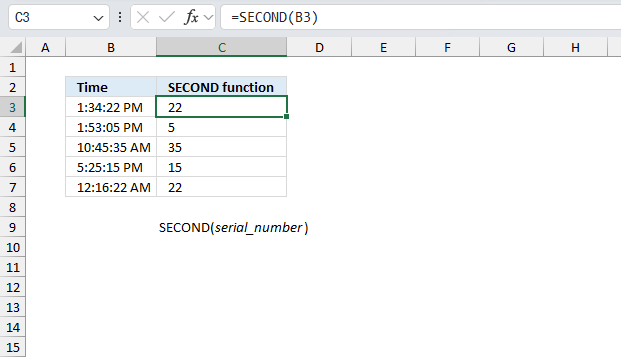
SECOND function returns an integer representing the second based on an Excel time value
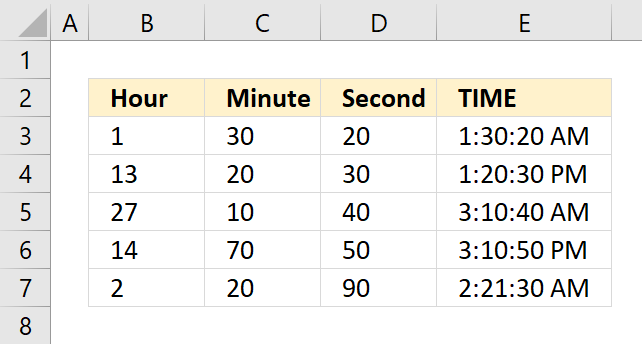
TIME function returns a decimal value between 0 (zero) representing 12:00:00 AM and 0.99988426 representing 11:59:59 P.M.
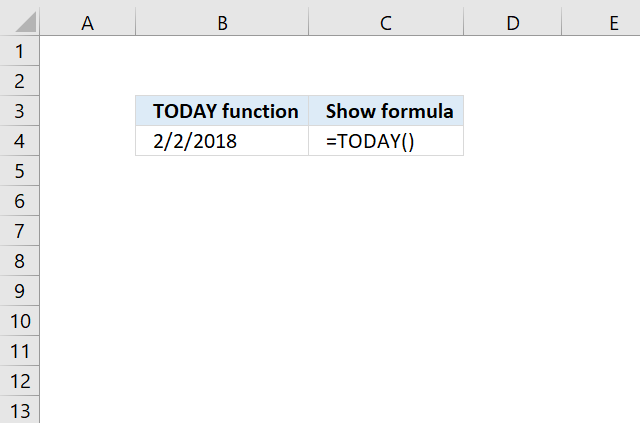
TODAY function returns the Excel date (serial number) of the current date.
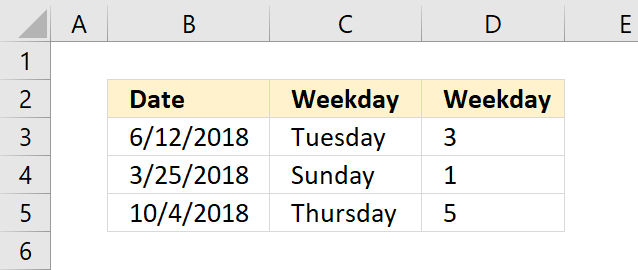
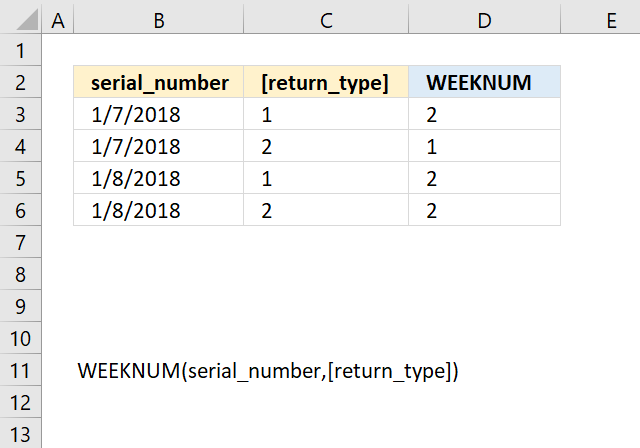
WEEKNUM function calculates a given date's week number based on a return_type parameter that determines which day the week begins.
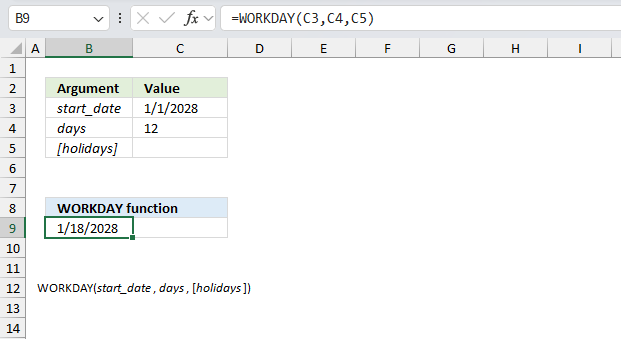
WORKDAY function returns a date based on a start date and a given number of working days (nonweekend and nonholidays).
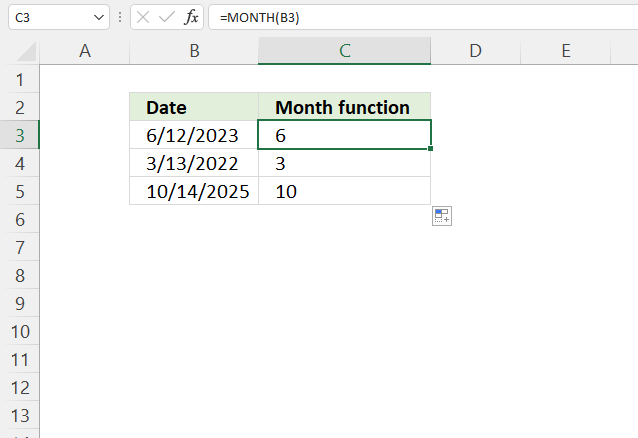
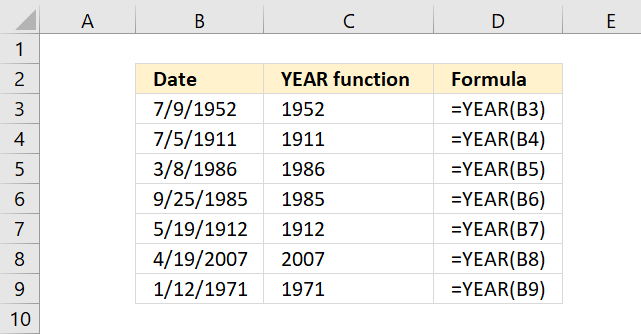
YEAR function converts a date to a number representing the year in the date.
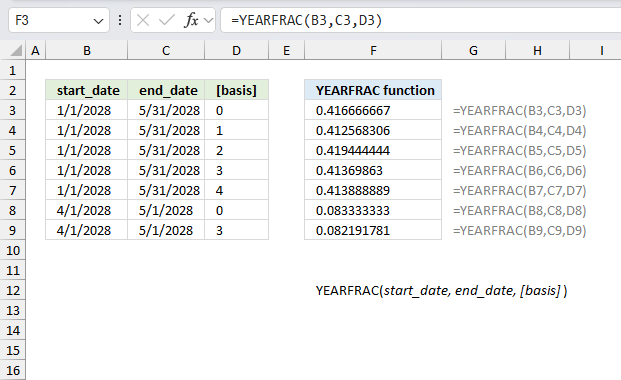
YEARFRAC function returns the fraction of the year based on the number of whole days between a start date and an end date.
Back to top
Engineering
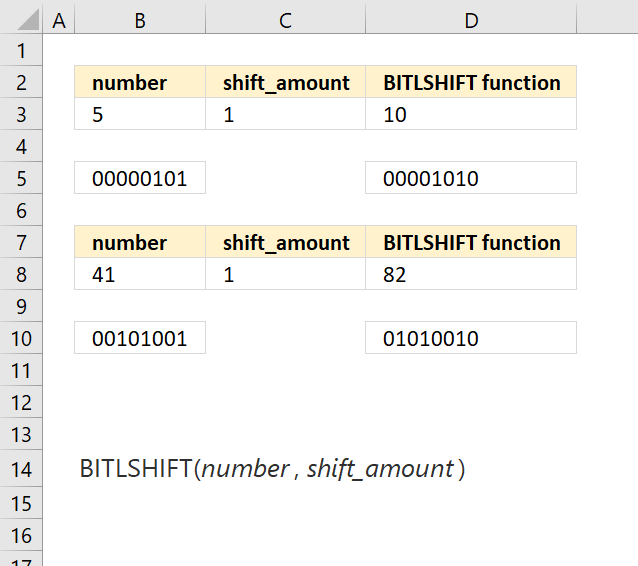
BITLSHIFT function calculates a number whose binary representation is shifted left by a specified number of bits.
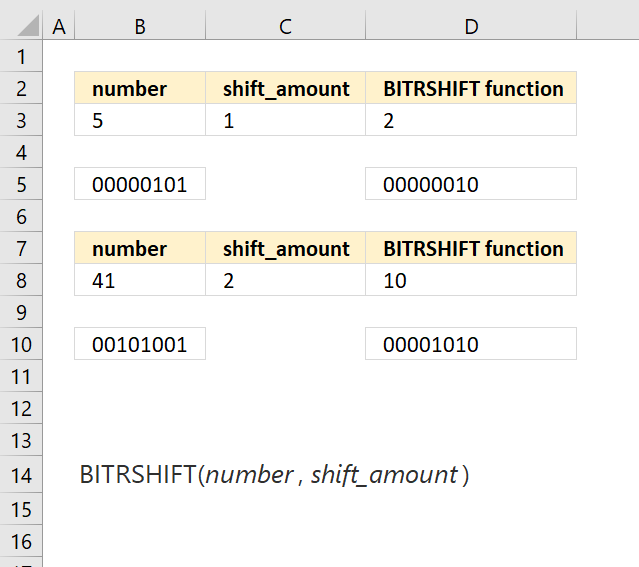
BITRSHIFT function calculates the number where the binary equivalent is shifted right by a specified number of bits and then converted back to a number.
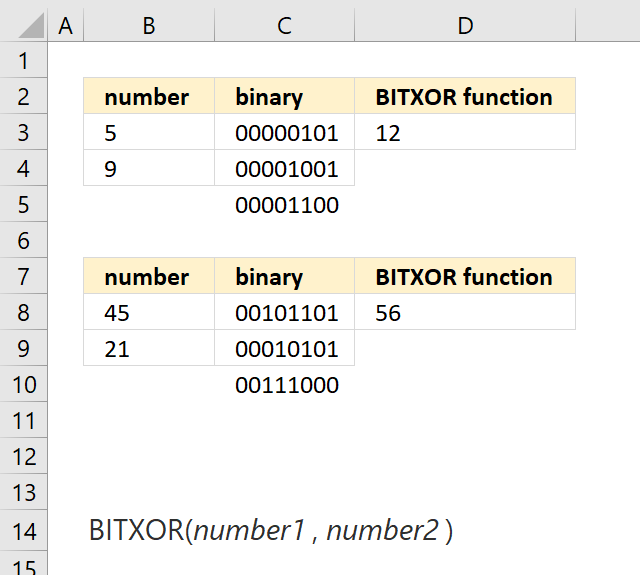
BITXOR function calculates a decimal number that is a result of a bitwise comparison "XOR" of two numbers.
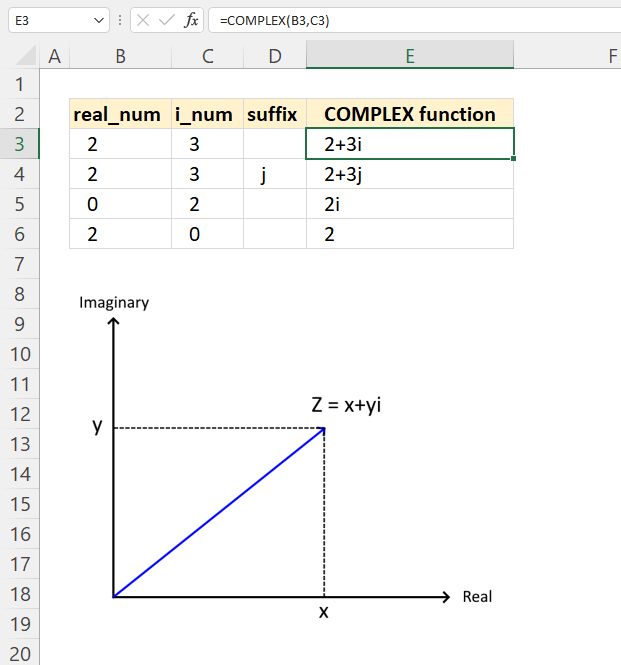
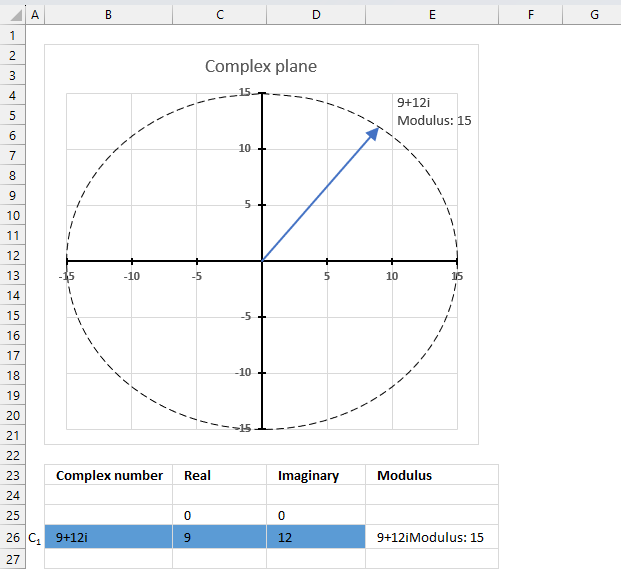
IMABS function calculates the absolute value (modulus) of a complex number in x + yi or x + yj text format.
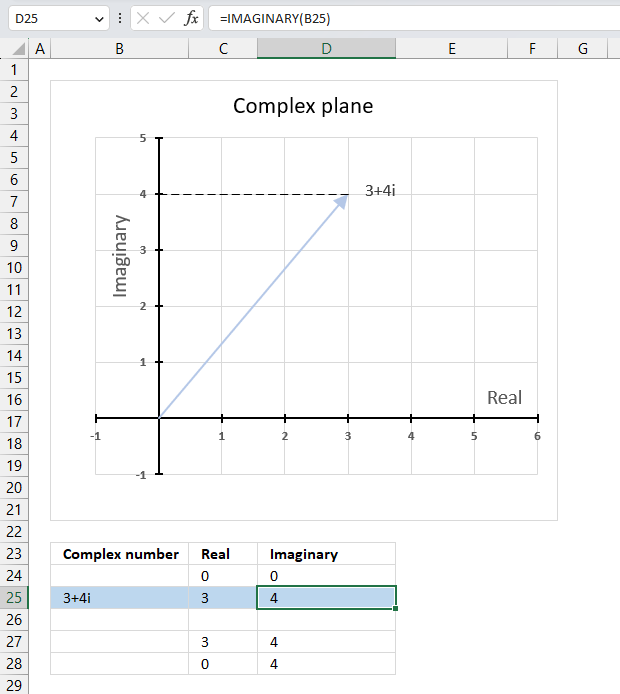
IMAGINARY function calculates the imaginary value of a complex number in x + yi or x + yj text format.
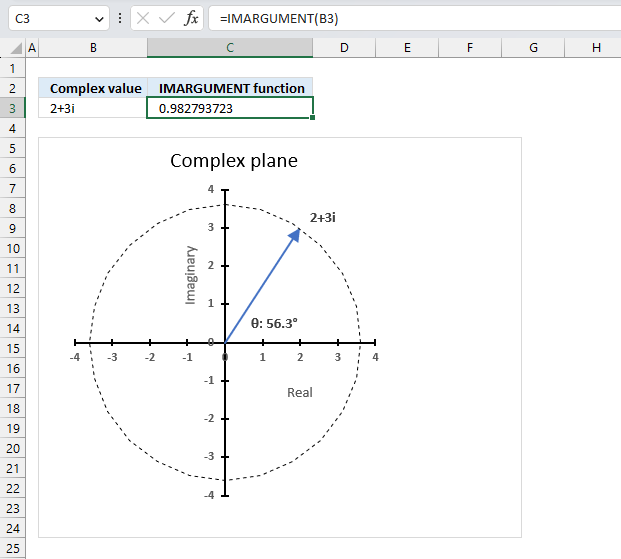
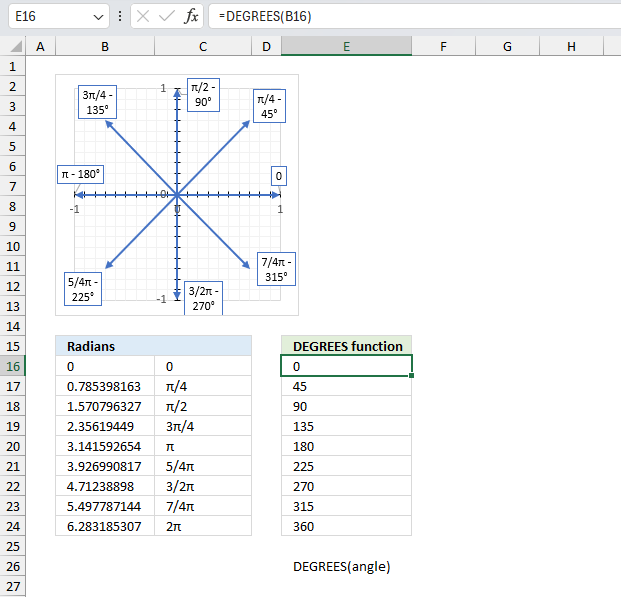
IMARGUMENT function calculates theta θ which is an angle displayed in radians based on complex numbers in rectangular form.
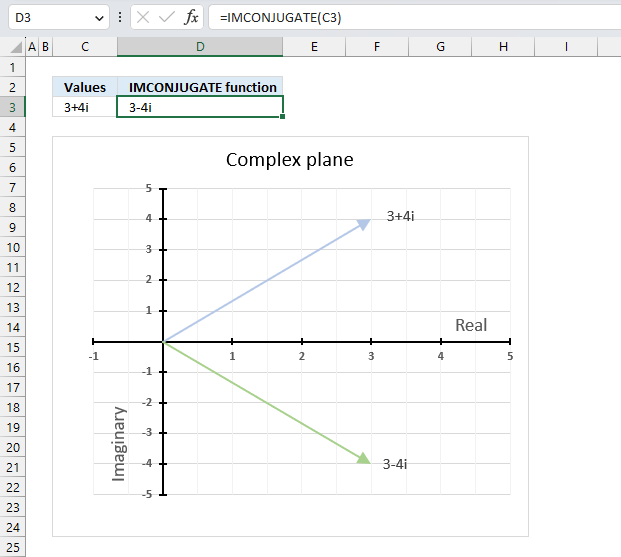
IMCONJUGATE function calculates the complex conjugate of a complex number in x + yi or x + yj text format.
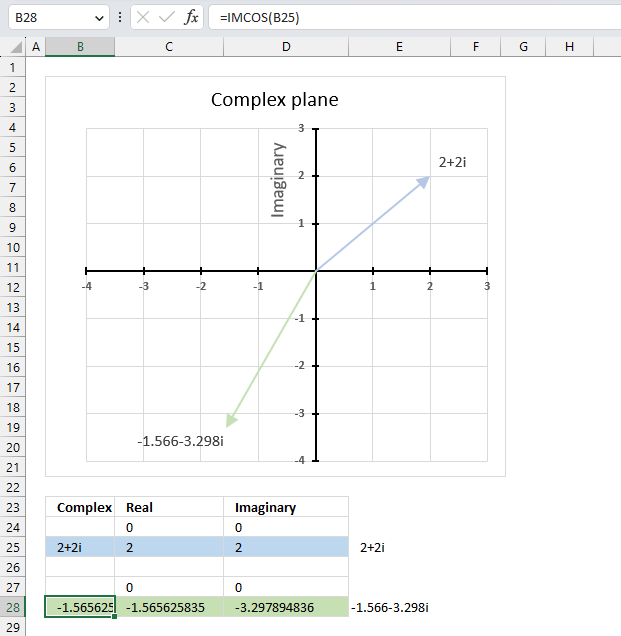
IMCOS function calculates the cosine of a complex number in x + yi or x + yj text format.
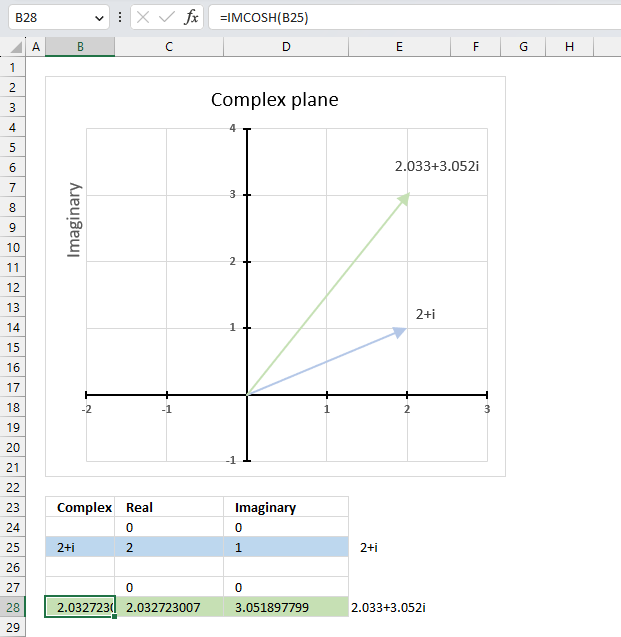
IMCOSH function calculates the hyperbole cosine of a complex number in x + yi or x + yj text format.
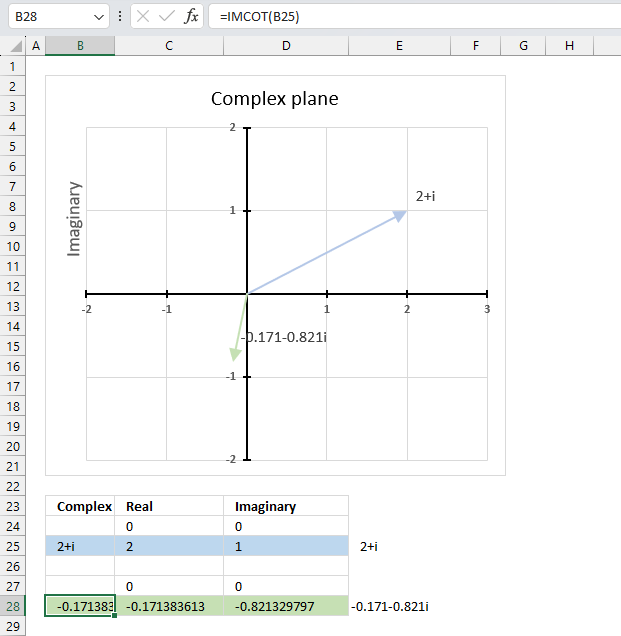
IMCOT function calculates the cotangent of a complex number in x + yi or x + yj text format.
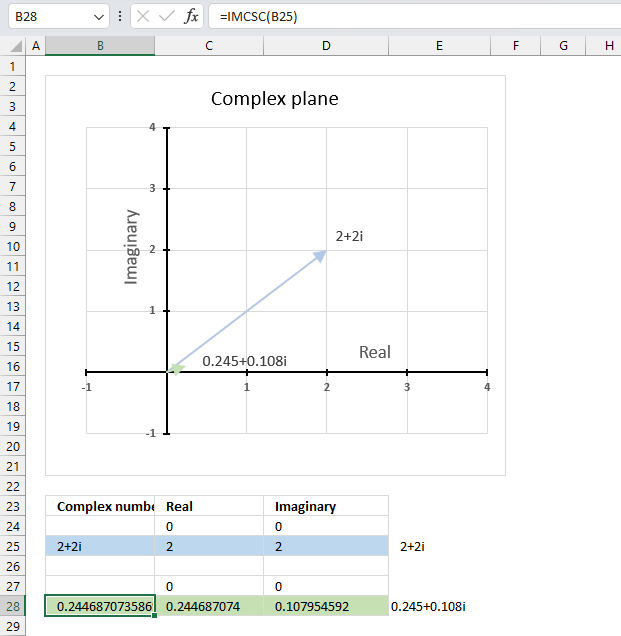
IMCSC function calculates the cosecant of a complex number in x + yi or x + yj text format.
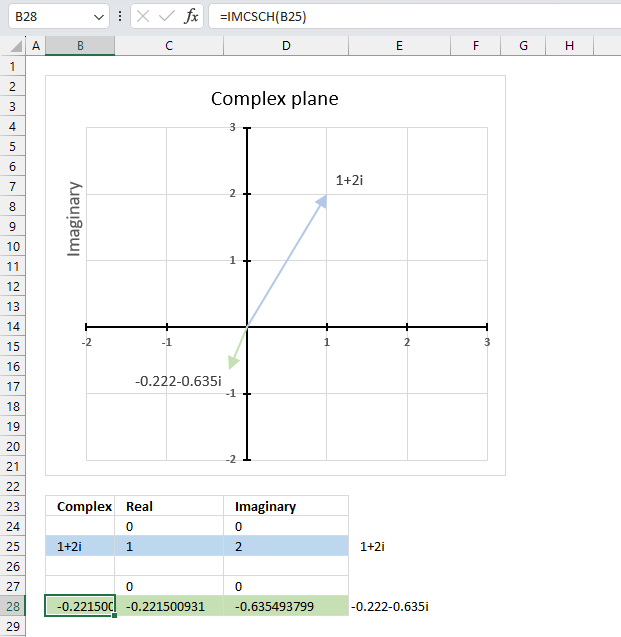
IMCSCH function calculates the hyperbolic cosecant of a complex number in x + yi or x + yj text format.
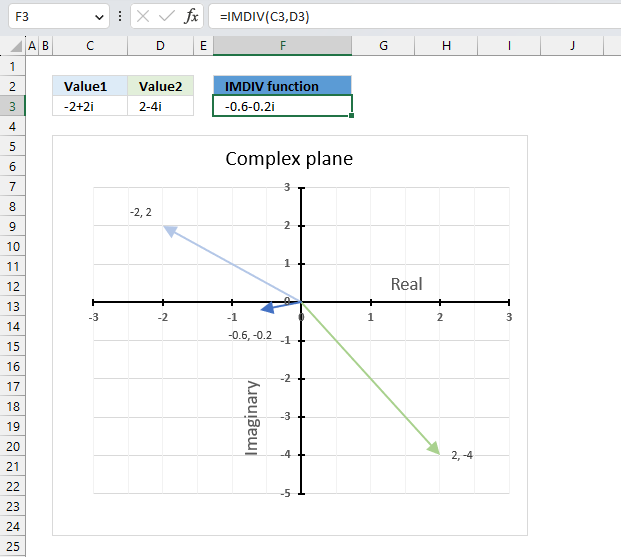
IMDIV function calculates the quotient of two complex numbers in x + yi or x + yj text format.
IMEXP function calculates the exponential of a complex number in x + yi or x + yj text format.
IMLN function calculates the natural logarithm of a complex number in x + yi or x + yj text format.
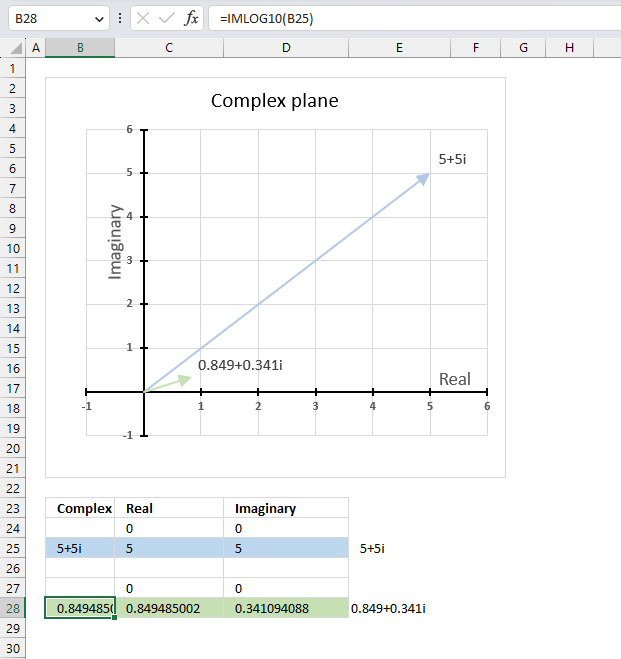
IMLOG10 function calculates the base 10 logarithm of a complex number in x + yi or x + yj text format.
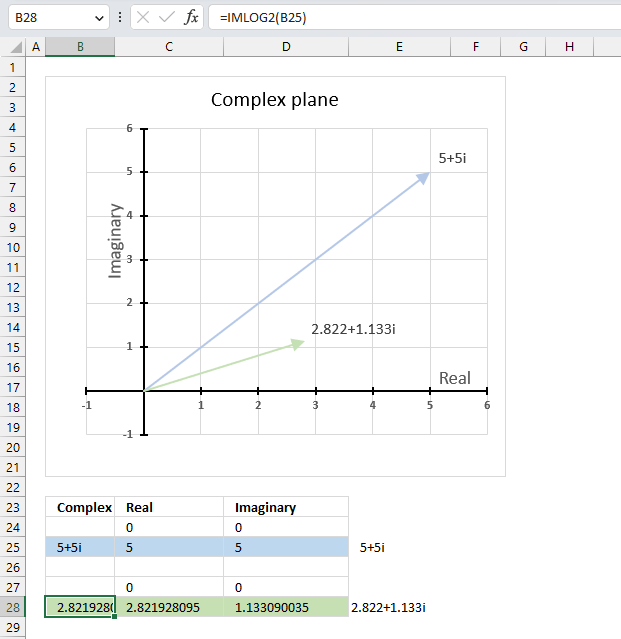
IMLOG2 function calculates the base 2 logarithm of a complex number in x + yi or x + yj text format.
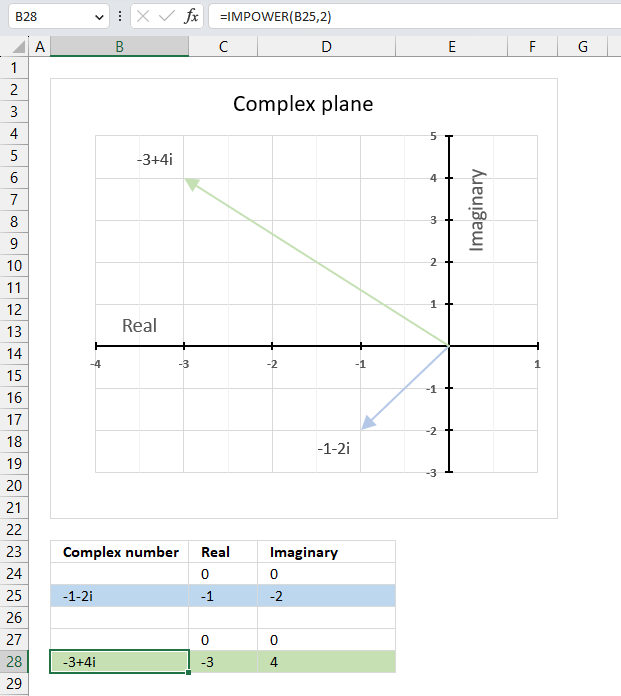
IMPOWER function calculates a complex number raised to a given power in x + yi or x + yj text format.
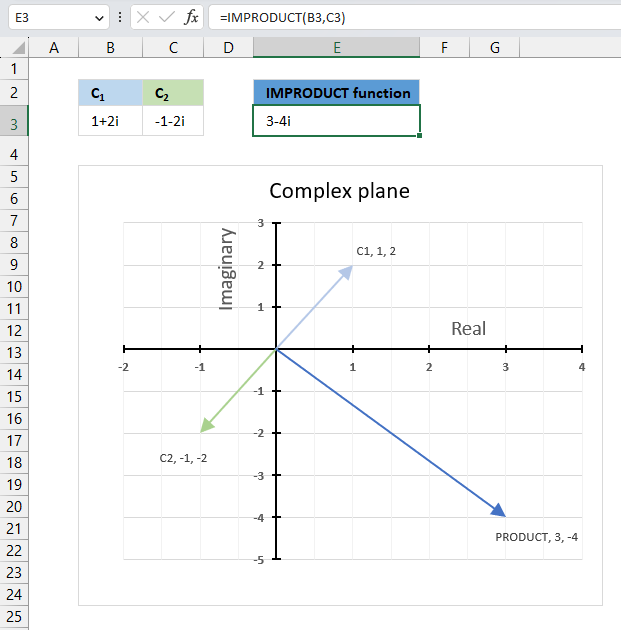
IMPRODUCT function calculates the product of complex numbers in x + yi or x + yj text format.
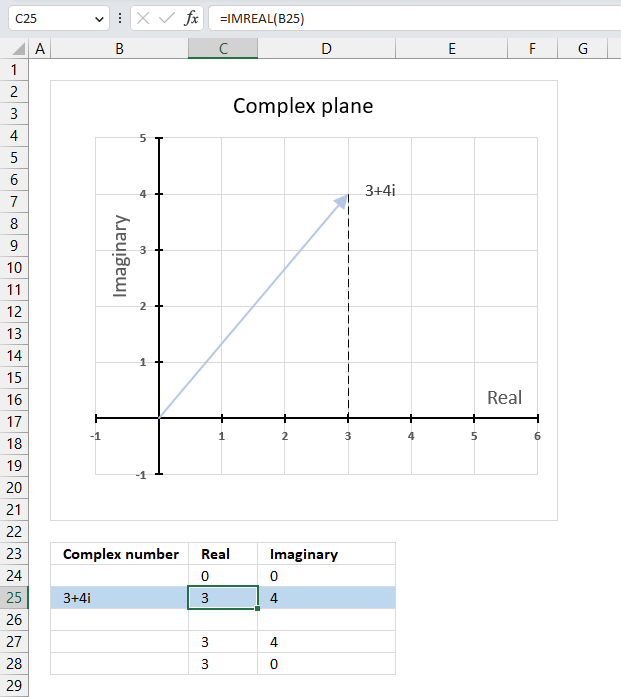
IMREAL function calculates the real coefficient of a complex number in x + yi or x + yj text format.
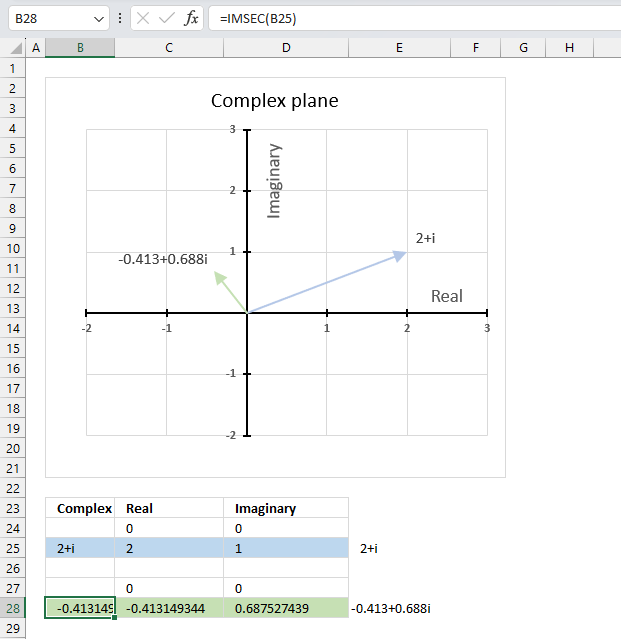
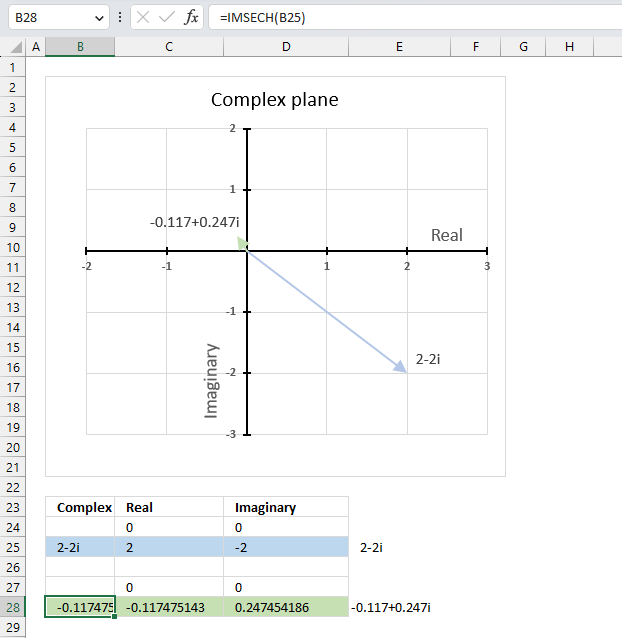
IMSEC function calculates the secant of a complex number in x + yi or x + yj text format.
IMSECH function calculates the hyperbolic secant of a complex number in x + yi or x + yj text format.
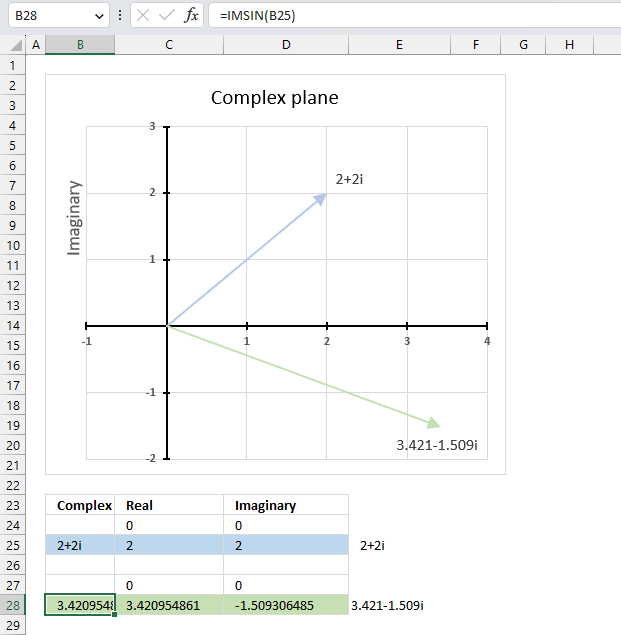
IMSIN function calculates the sine of a complex number in x + yi or x + yj text format.
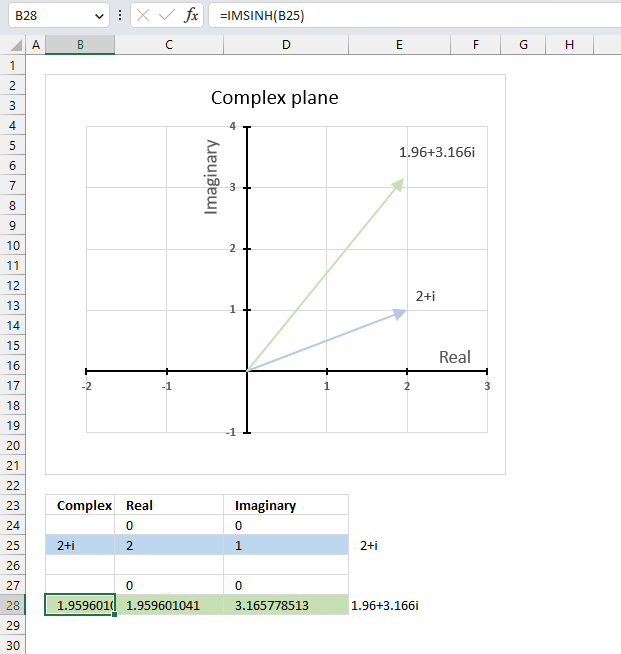
IMSINH function calculates the hyperbolic sine of a complex number in x + yi or x + yj text format.
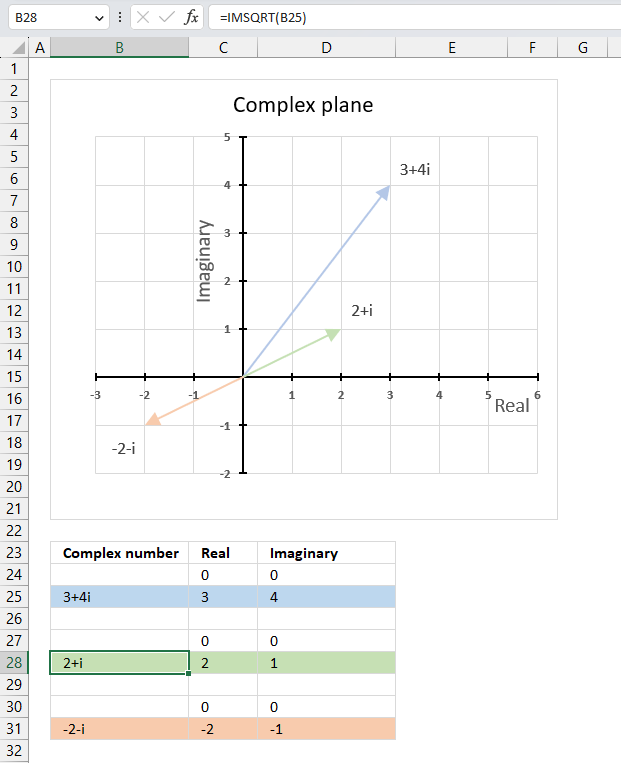
IMSQRT function calculates the square root of a complex number in x + yi or x + yj text format.
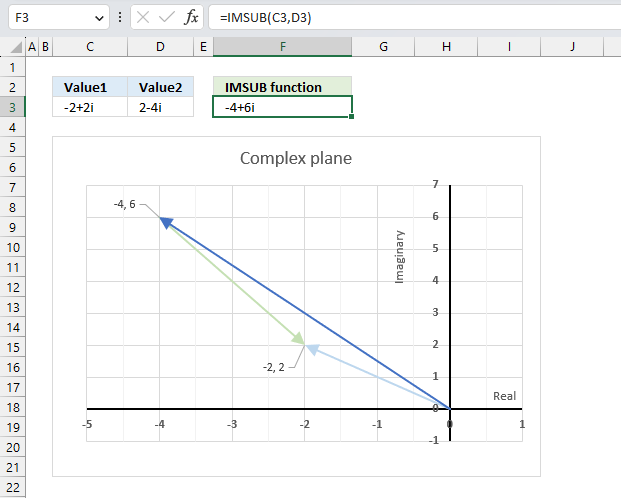
IMSUB function calculates the difference between two complex numbers in x + yi or x + yj text format.
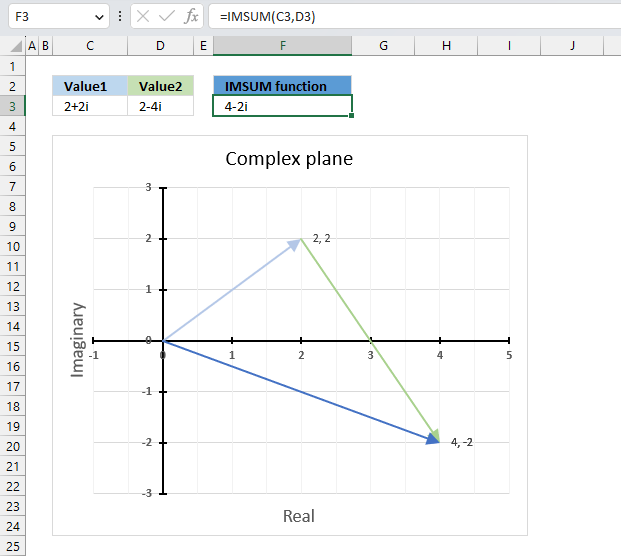
IMSUM function calculates the total of two or more complex numbers in x + yi or x + yj text format.
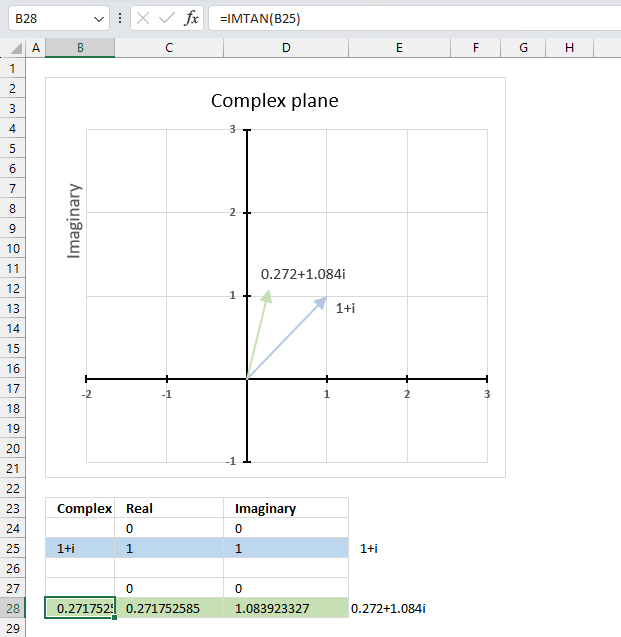
IMTAN function calculates the tangent of a complex number in x + yi or x + yj text format.
Back to top
Financial
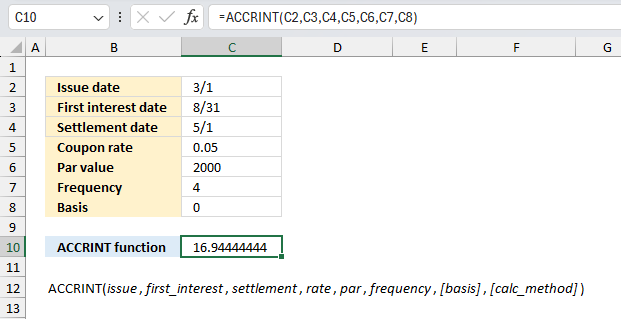
ACCRINT function calculates the accrued interest for a security that pays periodic interest.
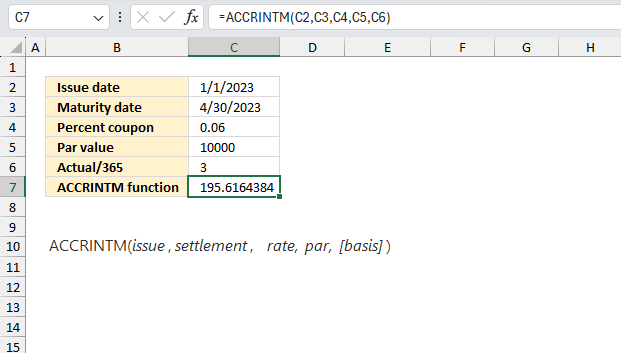
ACCRINTM function calculates the accrued interest for a security that pays interest at maturity.
CUMPRINC function calculates the accumulated principal based on a start and end period on a loan.
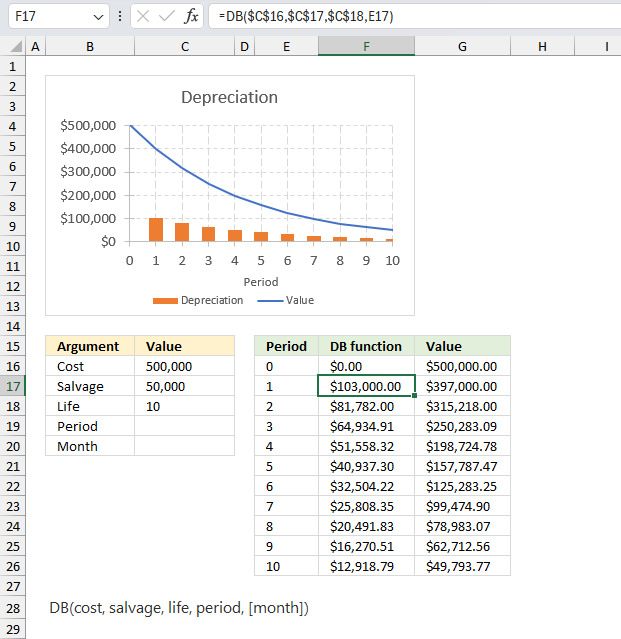
DB function calculates the depreciation of an asset for a given period using the fixed-declining balance method.
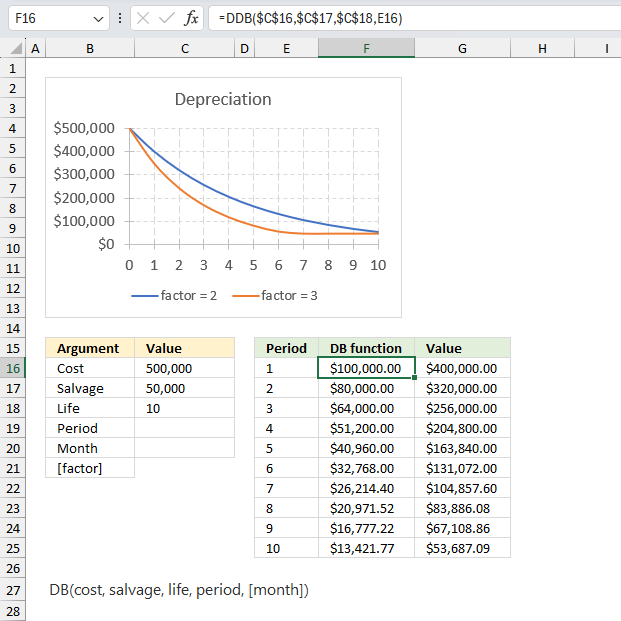
DDB function calculates the depreciation of an asset for a given period using the double-declining balance method or based on user input.
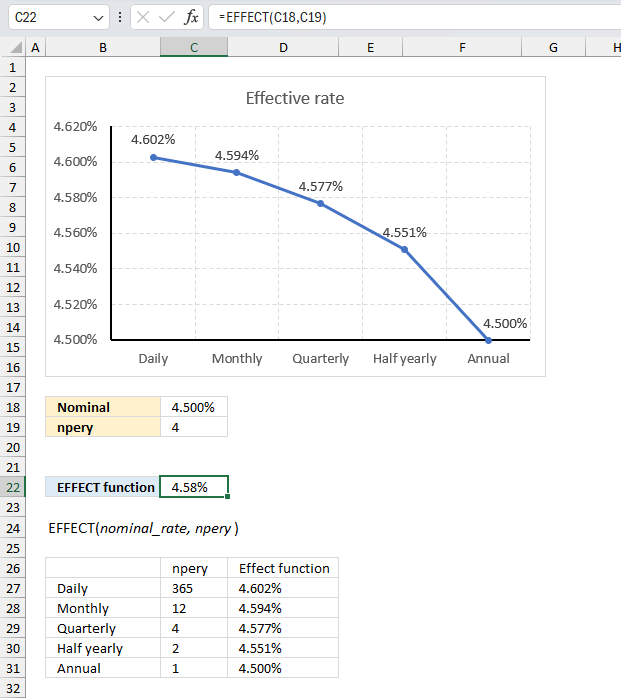
EFFECT function calculates the effective annual interest rate, given the nominal annual interest rate and the number of compounding periods per year.
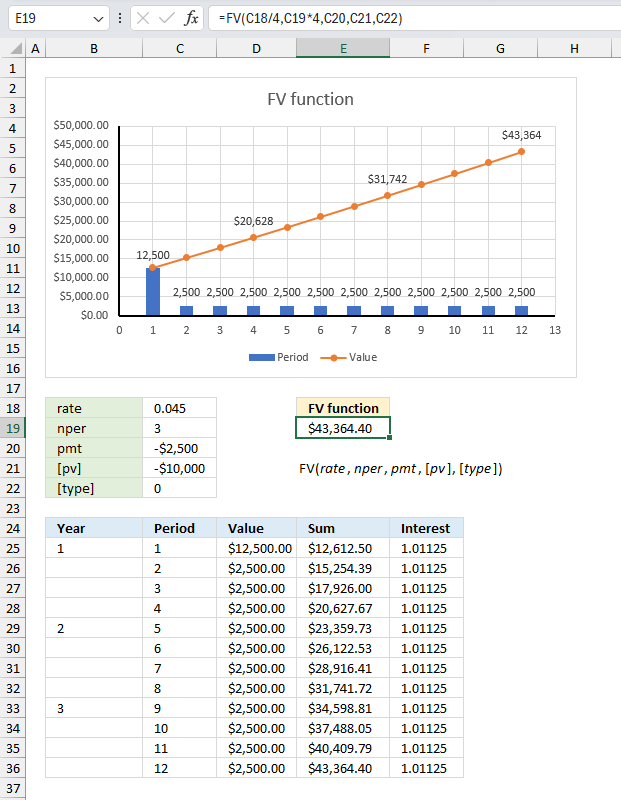
FV function returns the future value of an investment based on a constant interest rate.
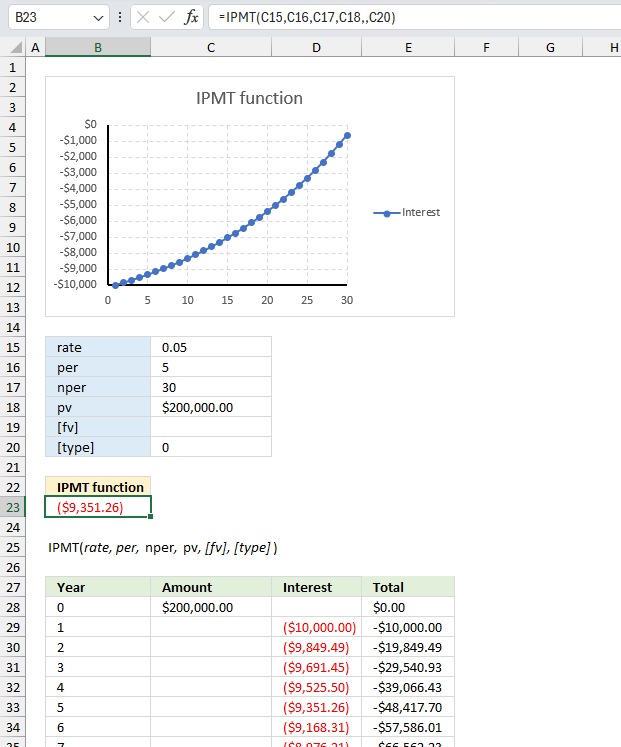
IPMT function calculates the interest payment for a specific period for an investment based on repeated constant payments and a constant interest rate.
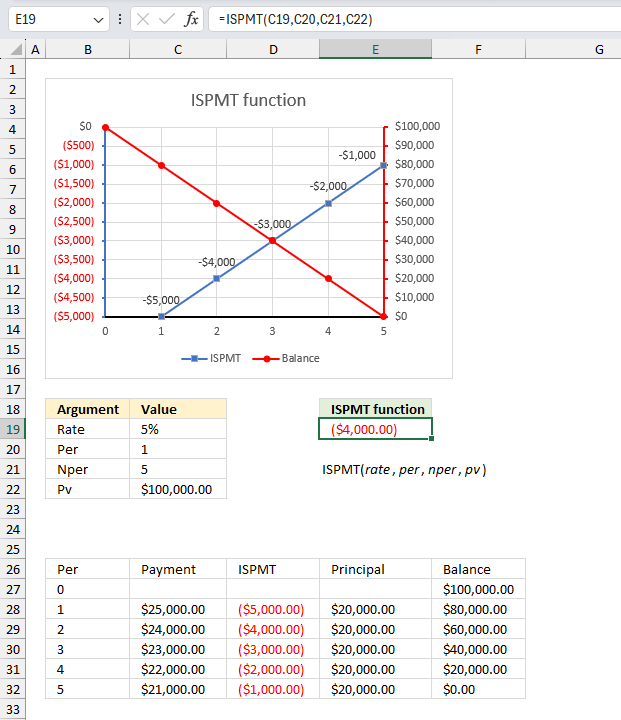
ISPMT function calculates the interest paid during a specific period of an investment.
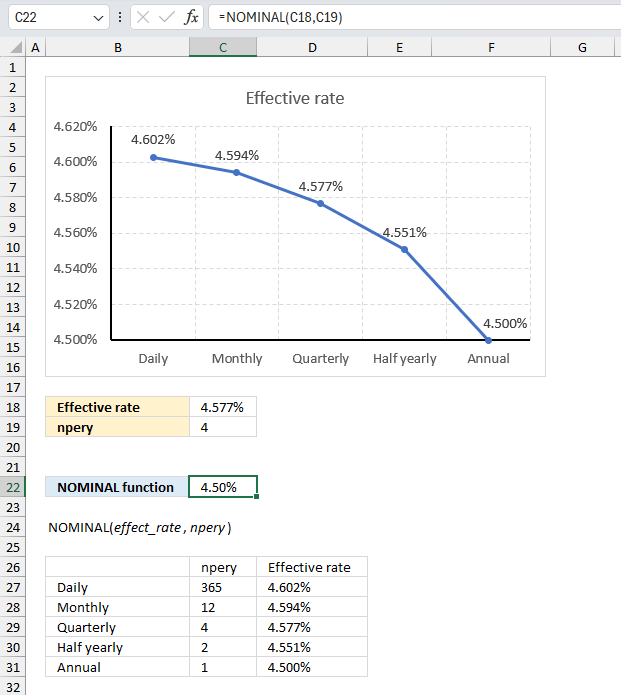
NOMINAL function calculates the nominal annual interest rate based on the effective rate and the number of compounding periods per year.
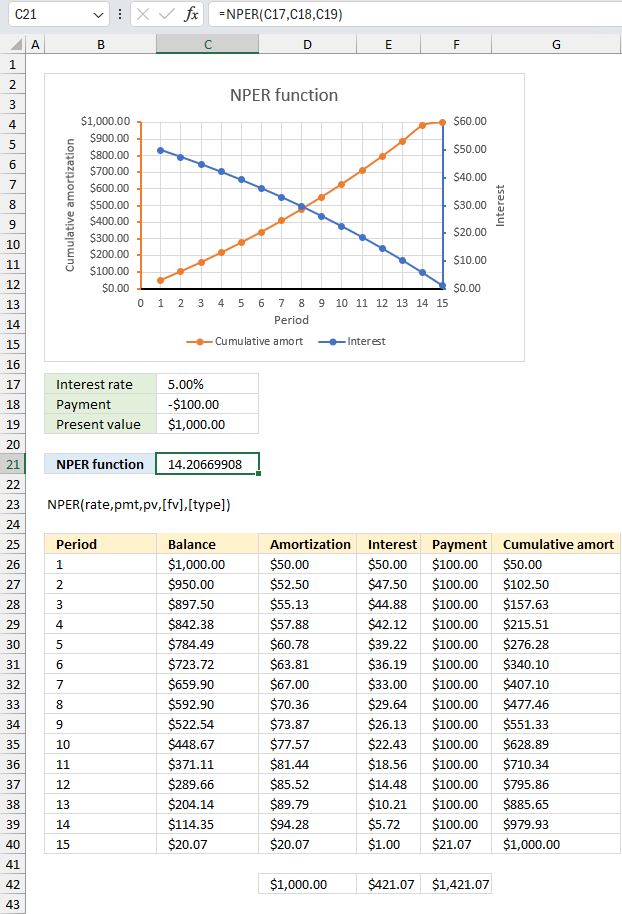
NPER function calculates the number of periods for an investment based on periodic, constant payments and a fixed interest rate.
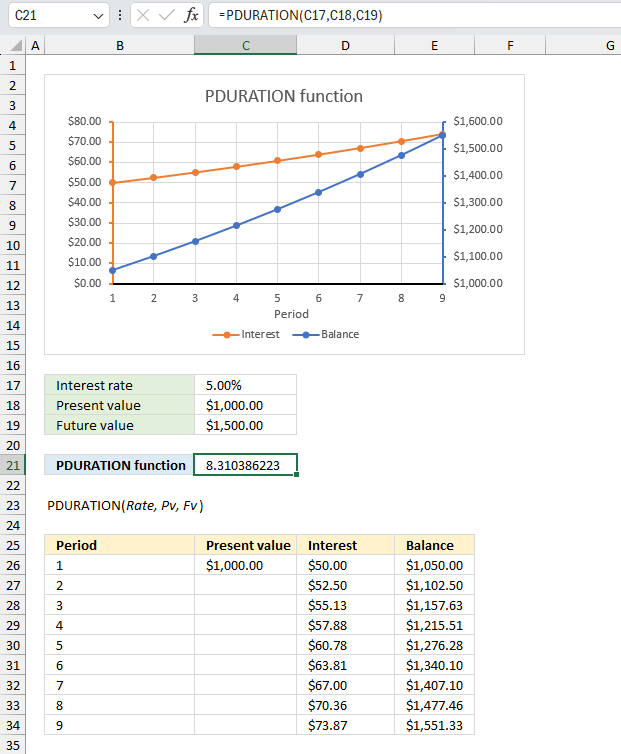
PDURATION function calculates how many periods required by an investment to reach a given amount based on a rate in percentage.
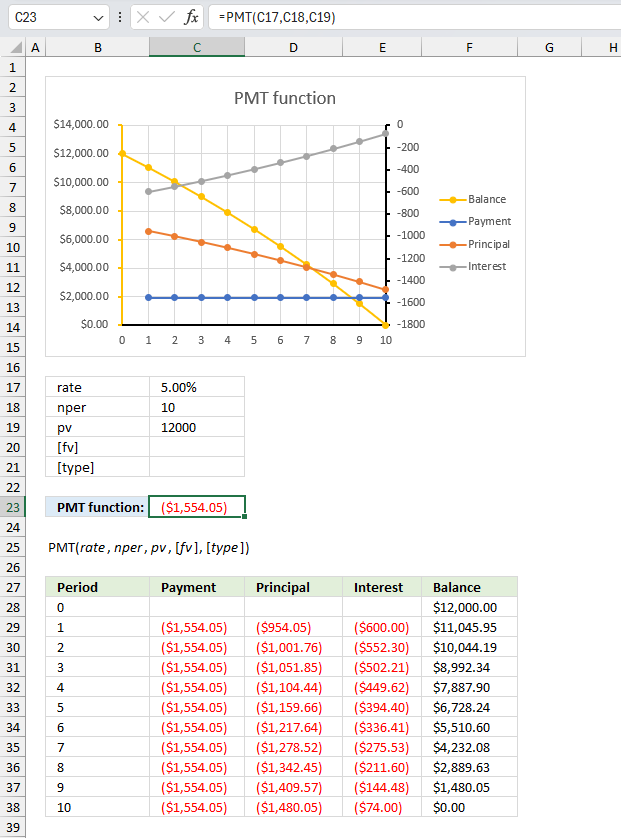
PMT function returns the payment needed for borrowing a fixed sum of money based on constant payments (annuity) and interest rate.
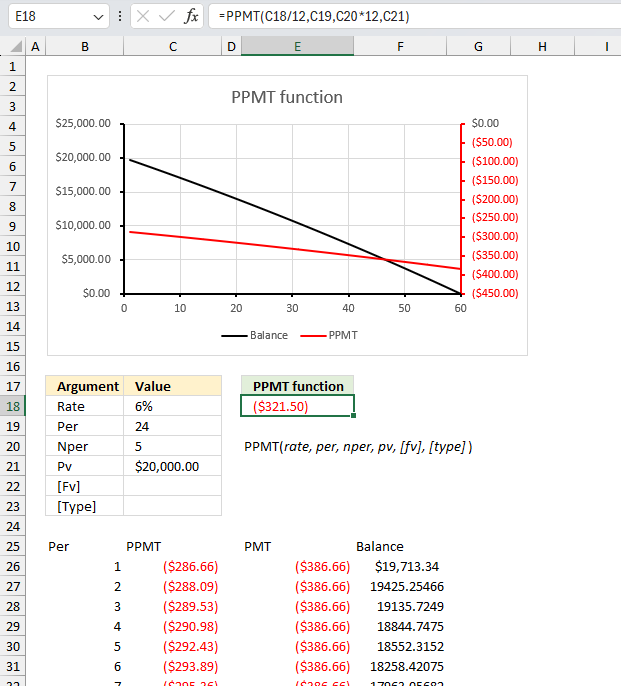
PPMT function calculates the principal payment for a specific period for an investment based on repeated constant payments and a constant interest rate.
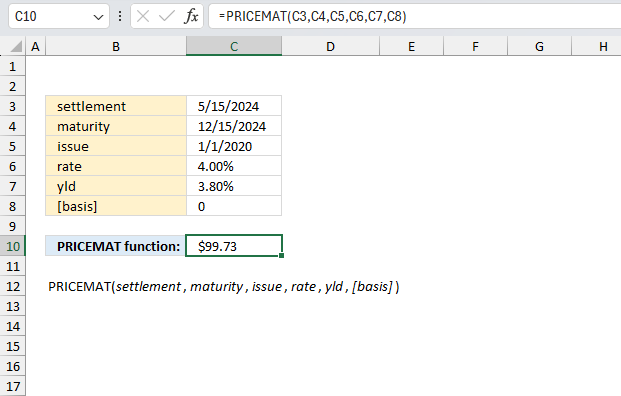
PRICEMAT function calculates the price per $100 nominal value of a bond that pays interest at maturity.
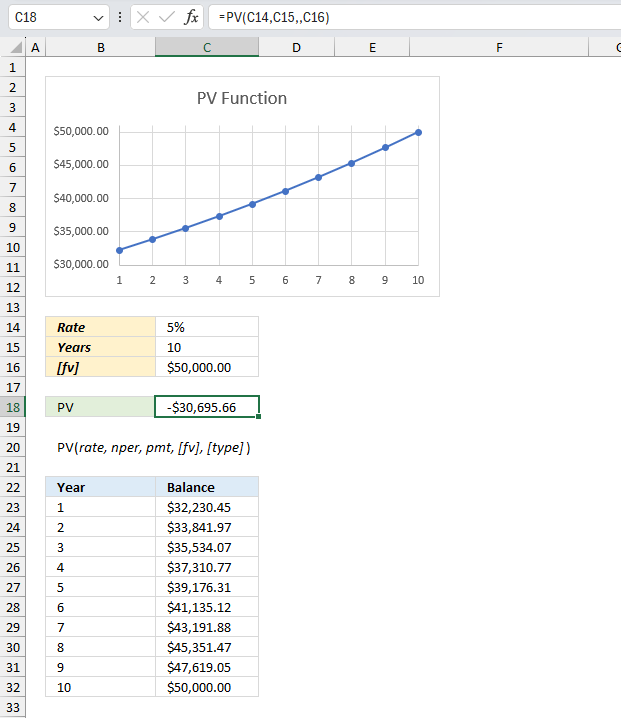
PV function calculates the net present value for an investment or loan.
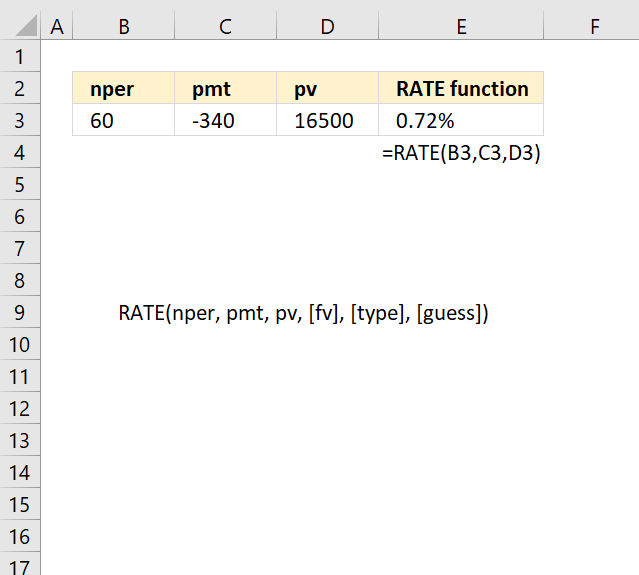
RATE function returns the interest rate per period of an annuity.
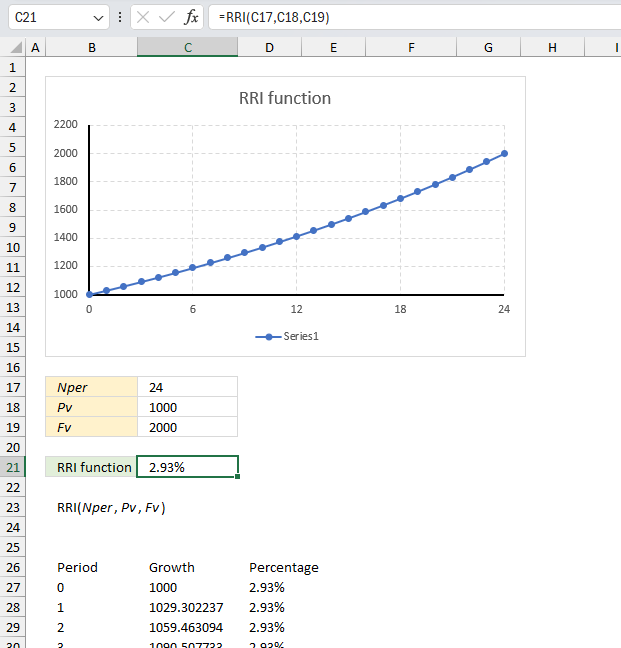
RRI function calculates the growth of an investment in percent per period.
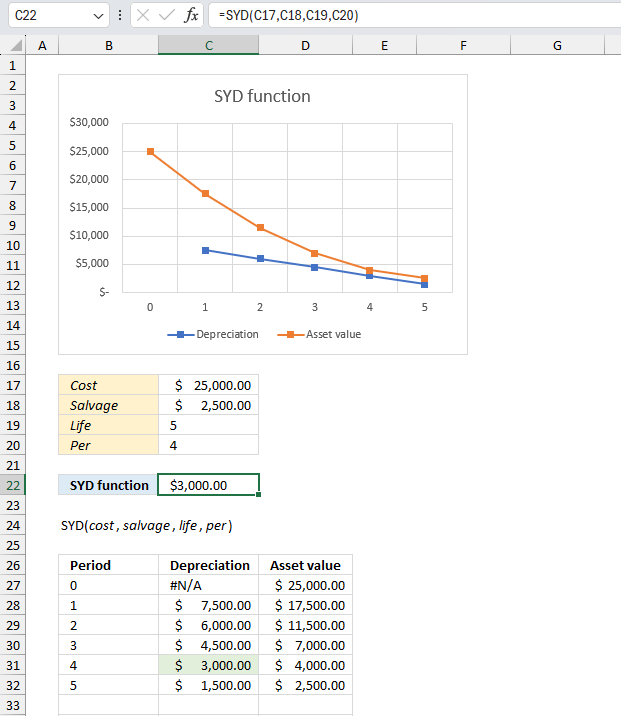
SYD function calculates the yearly asset depreciation of a given year.
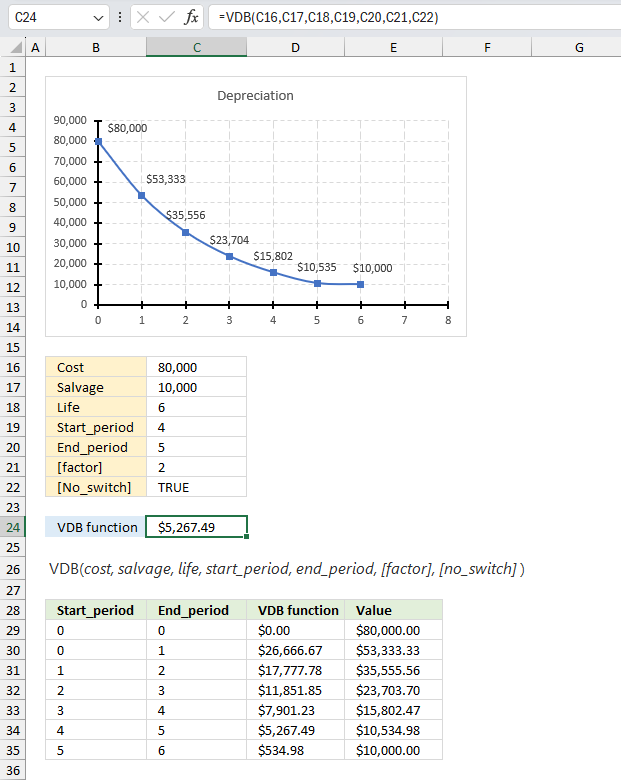
VDB function calculates the depreciation of an asset for a given period using the double-declining balance method or based on user input, you may use partial periods in this function.
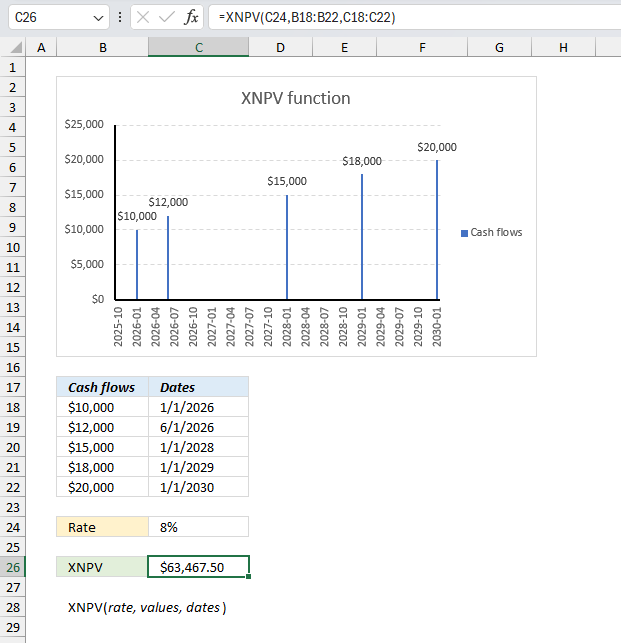
XNPV function calculates net present value for cash flows that may or may not be periodic
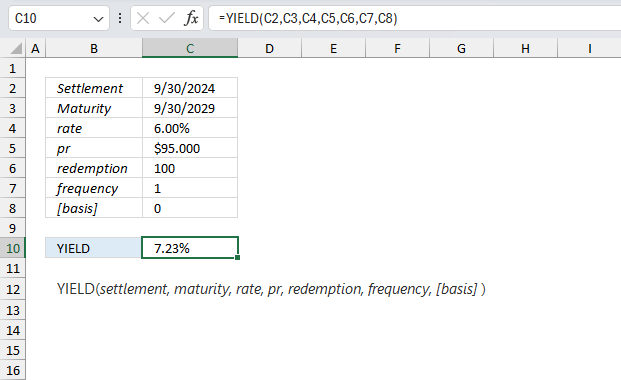
YIELD function calculates the yield for a security that pays interest. The YIELD function is designed to calculate the bond yield.
Back to top
Information
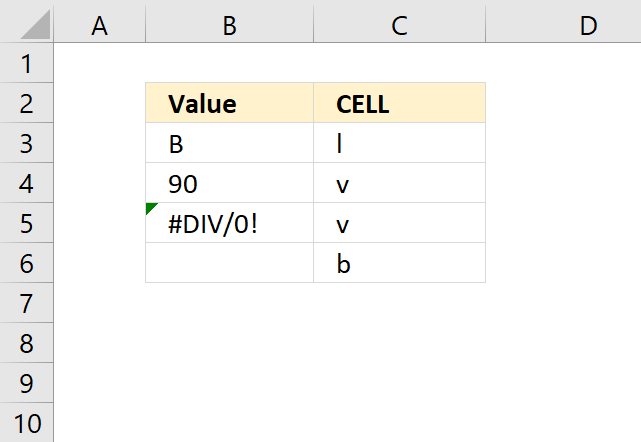
CELL function gets information about the formatting, location, or the contents of a cell.
INFO function returns information about the current operating environment, file path, number of active worksheets, Excel version etc.
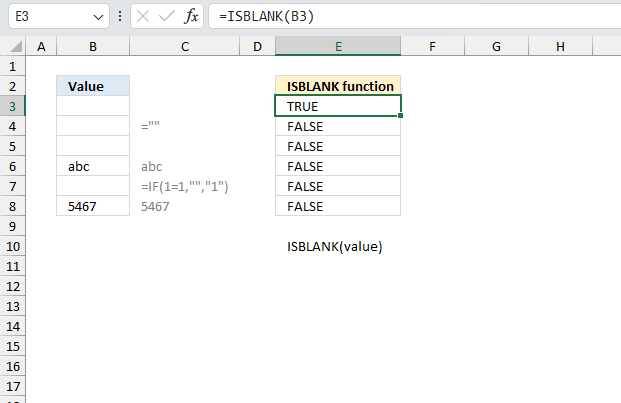
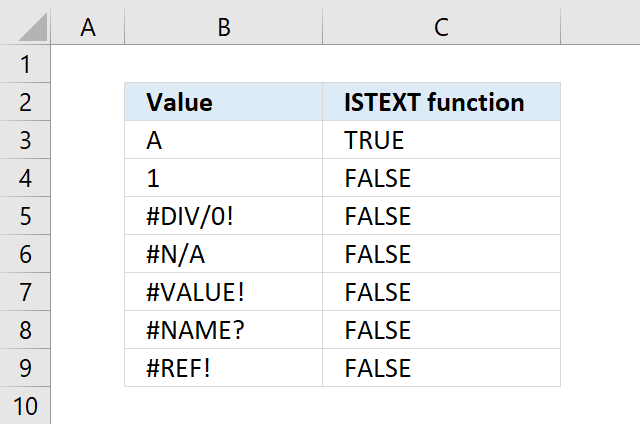
ISBLANK function returns TRUE if the argument is an empty cell, returns FALSE if not.
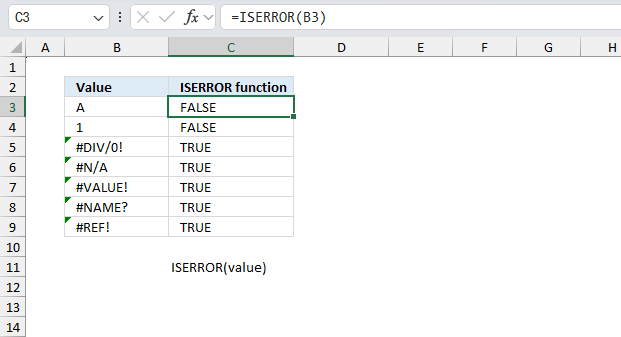
ISERR function returns TRUE if a cell returns an error, except error value #N/A.
ISFORMULA function returns TRUE if a cell contains a formula, FALSE if text, number or boolean value.
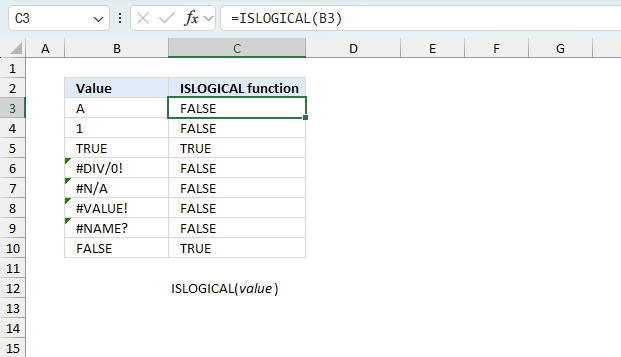
ISLOGICAL function returns TRUE if value is boolean. A boolean value is either TRUE or FALSE.
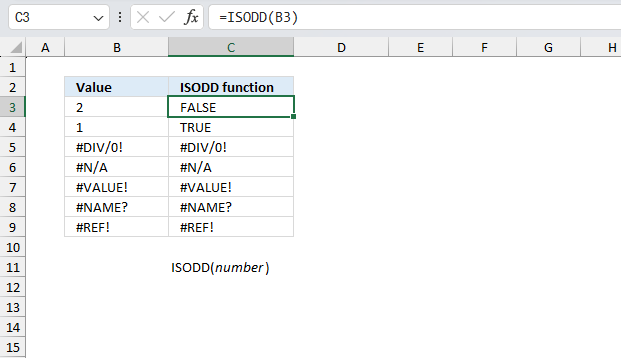
ISODD function returns TRUE if a cell contains an odd number, FALSE if even number.
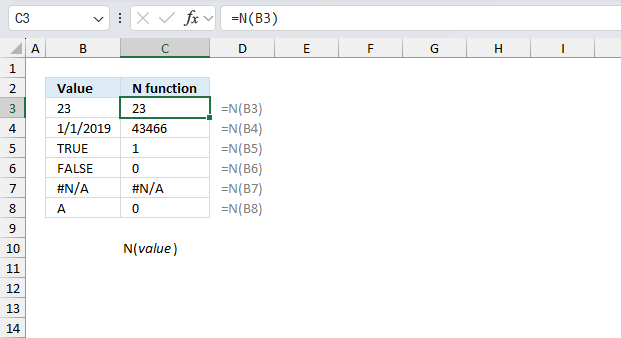
N function returns a value converted into a number.
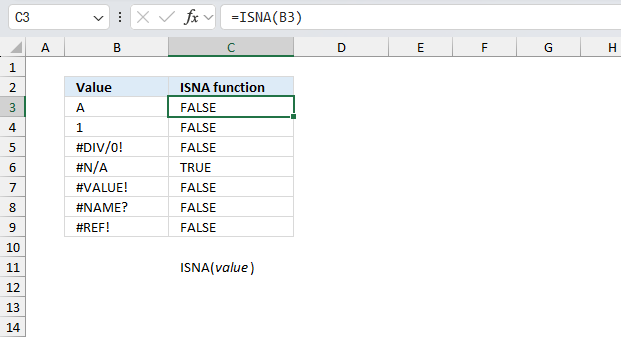
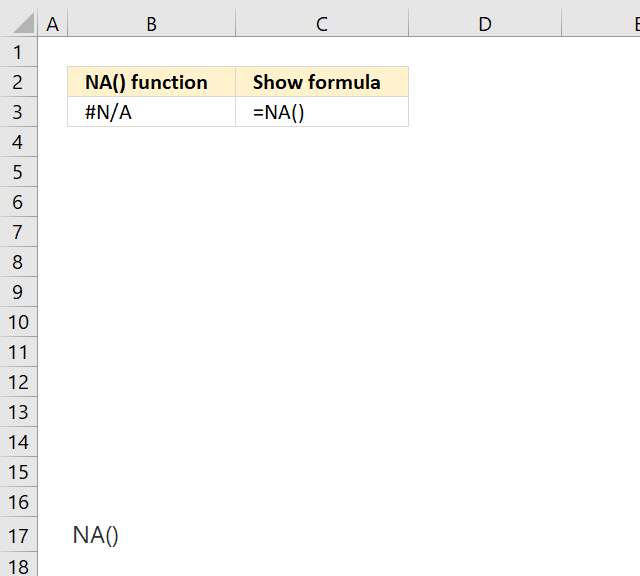
NA function returns the error value #N/A meaning "value is not available".
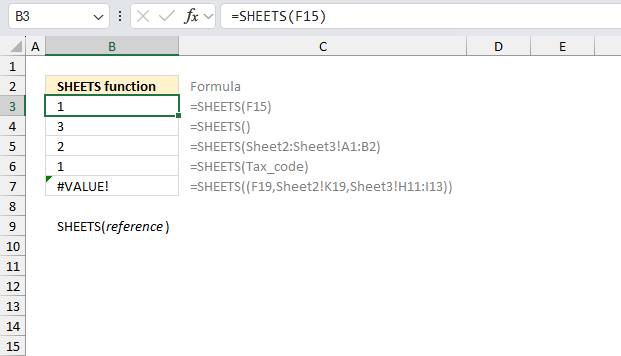
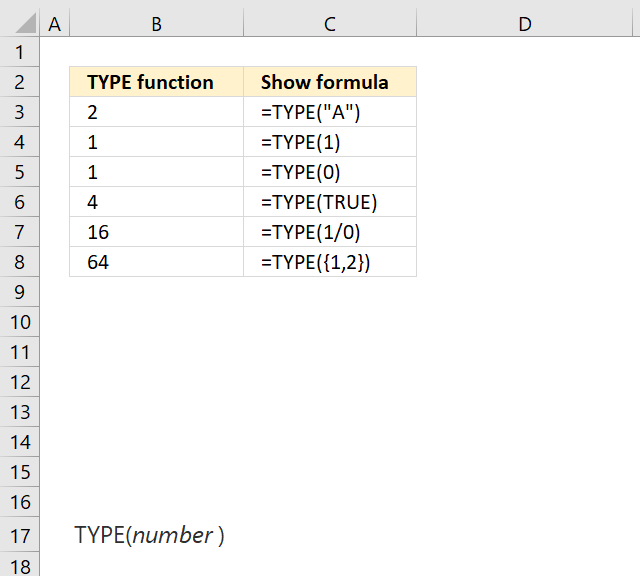
TYPE function use TYPE to find out what type of data is returned by a function or formula.
Back to top
Logical
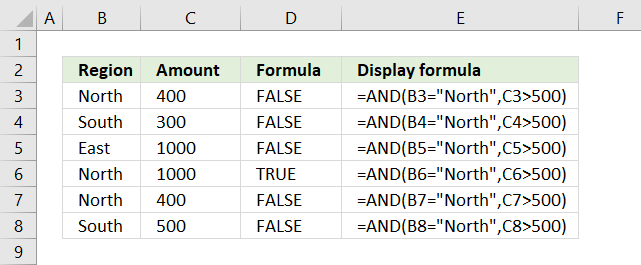
AND function perform a logical test in each argument and if all arguments return TRUE the AND function returns TRUE.
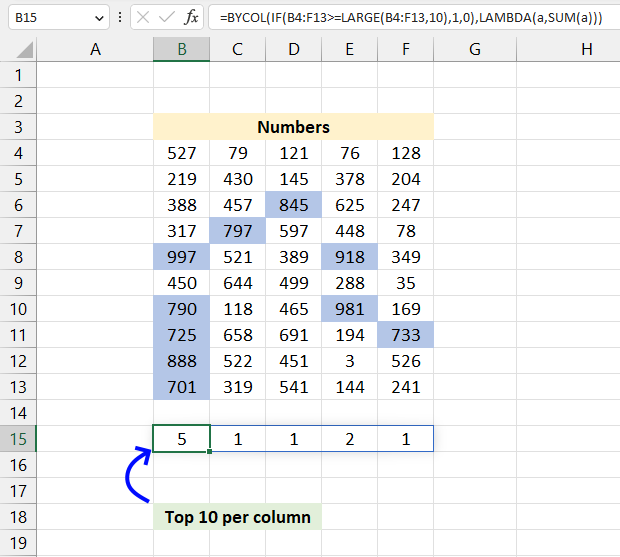
BYCOL function passes all values in a column based on an array to a LAMBDA function, the LAMBDA function calculates new values based on a formula you specify.
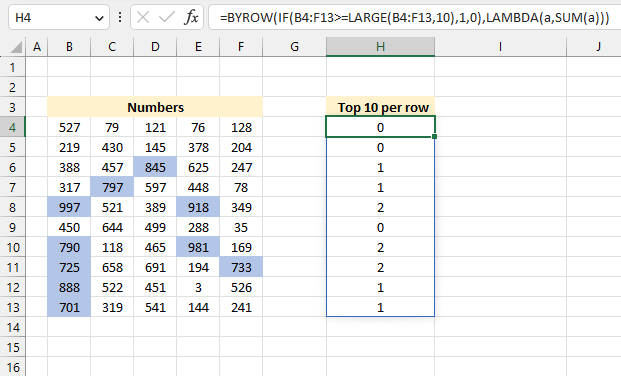
BYROW function puts values from an array into a LAMBDA function row-wise.
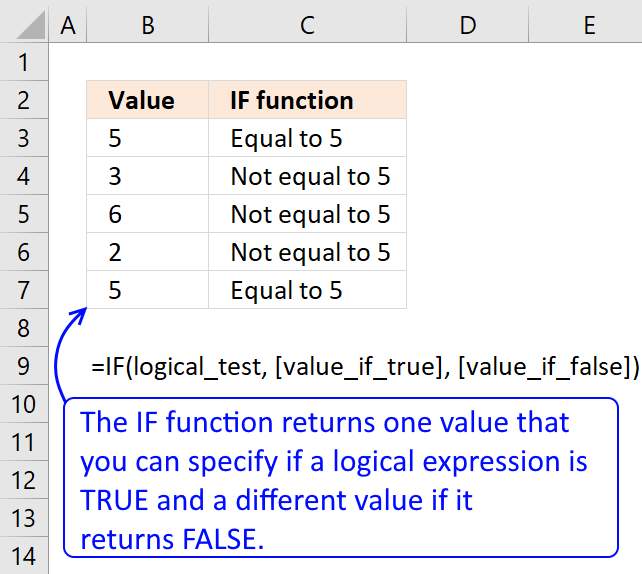
IF function returns one value if the logical test is TRUE and another value if the logical test is FALSE.
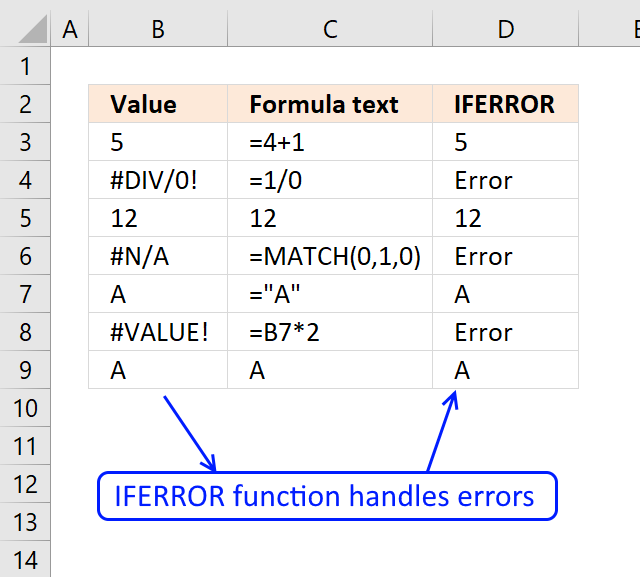
IFERROR function if the value argument returns an error, the value_if_error argument is used. If the value argument does NOT return an error, the IFERROR function returns the value argument.
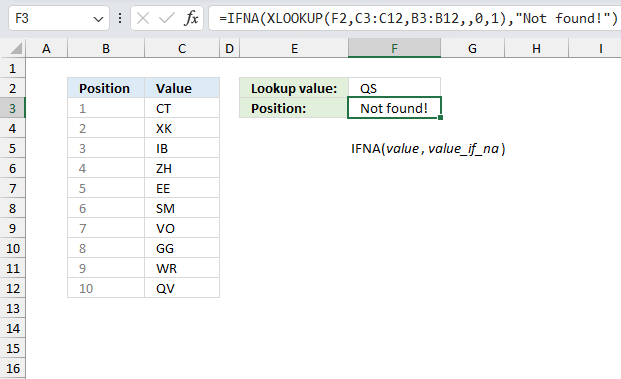
IFNA function handles #N/A errors only, it returns a specific value if the formula returns a #N/A error.
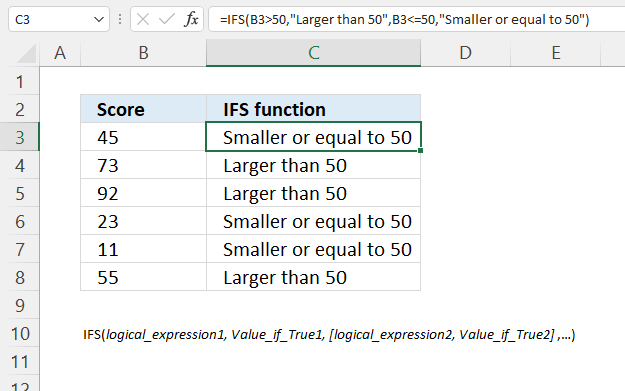
IFS function checks whether one or more conditions are met and returns a value that corresponds to the first TRUE condition.
MAKEARRAY function returns an array with a specific number of rows and columns calculated by applying a LAMBDA function.
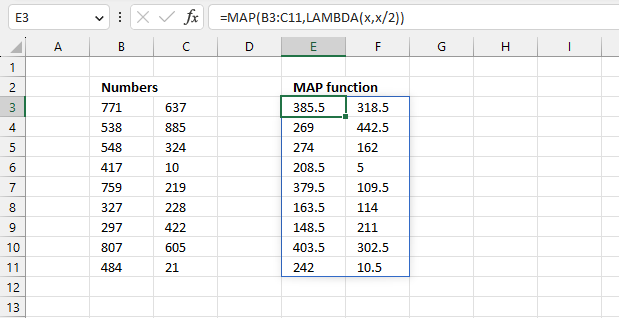
MAP function passes all values in an array to a LAMBDA function, the LAMBDA function calculates new values based on a formula you specify. It then returns an array with the same size as the original array.
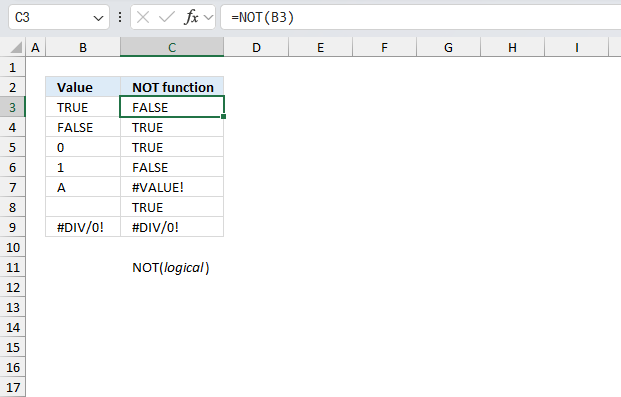
NOT function returns the boolean opposite to the given argument.
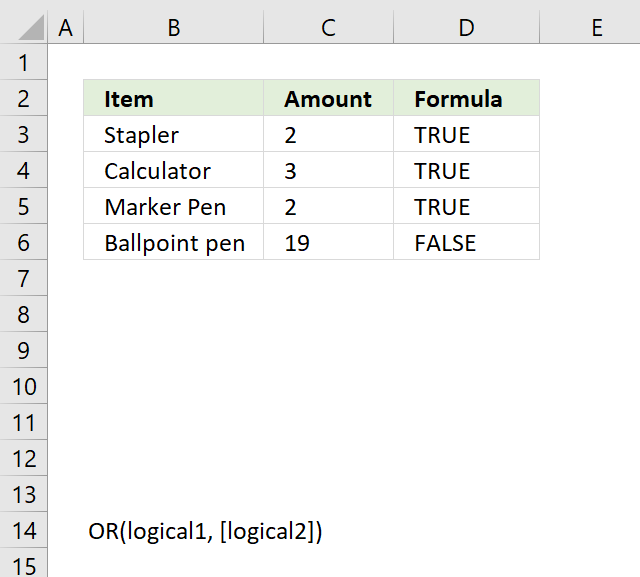
OR function evaluates a logical expression in each argument and if at least one argument returns TRUE the OR function returns TRUE. If all arguments return FALSE the OR function also returns FALSE.
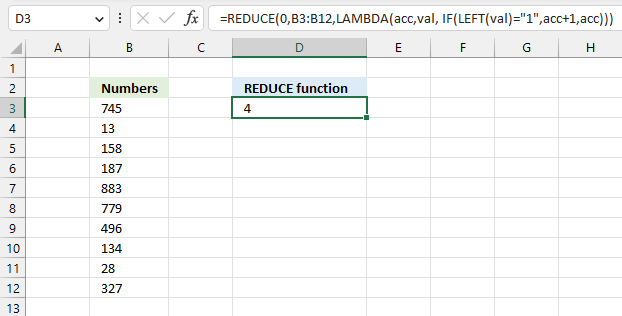
REDUCE function shrinks an array to an accumulated value, a LAMBDA function is needed to properly accumulate each value in order to return a total.
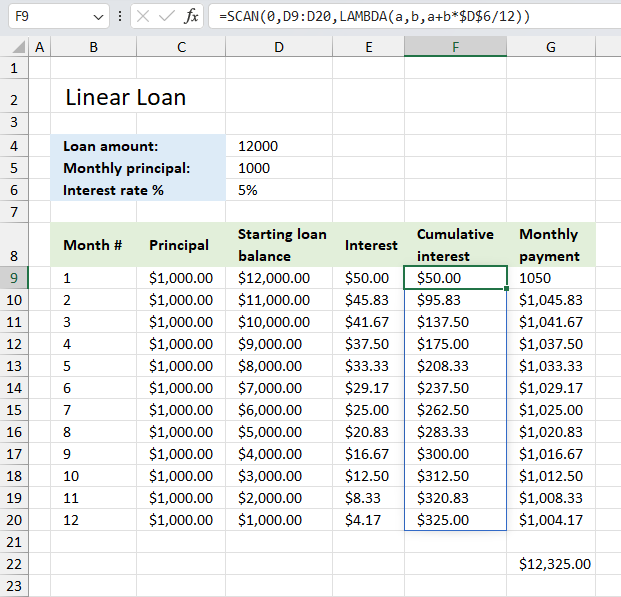
SCAN function passes values in an array to a LAMBDA function, the LAMBDA function calculates new values based on a formula you specify. It then returns an array with the same size as the original array using an accumulator parameter.
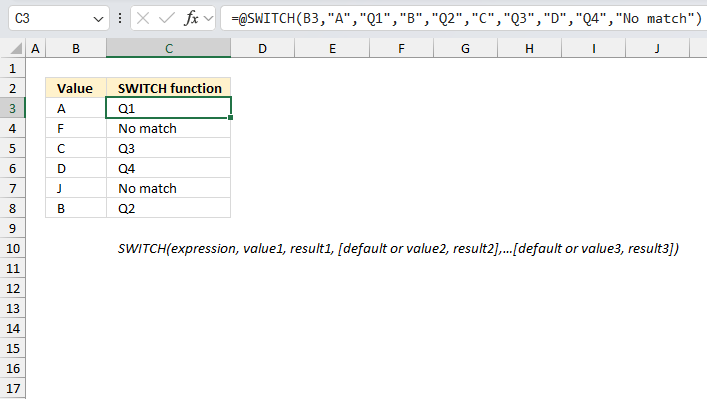
SWITCH function returns a given value determined by an expression and a list of values.
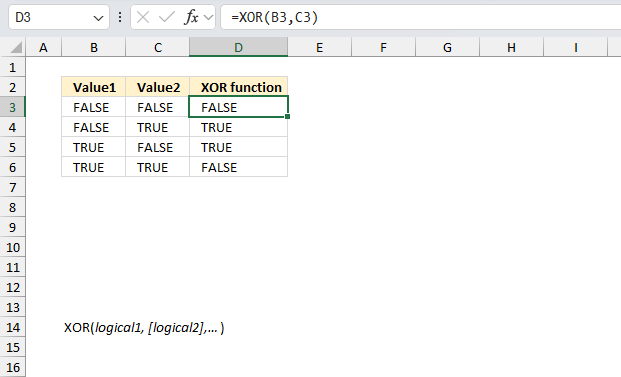
XOR function calculates the logical exclusive OR meaning if at least one of the arguments evaluates to TRUE then the XOR returns TRUE. All arguments must be evaluated to FALSE for the XOR function to return FALSE.
Back to top
Lookup and reference
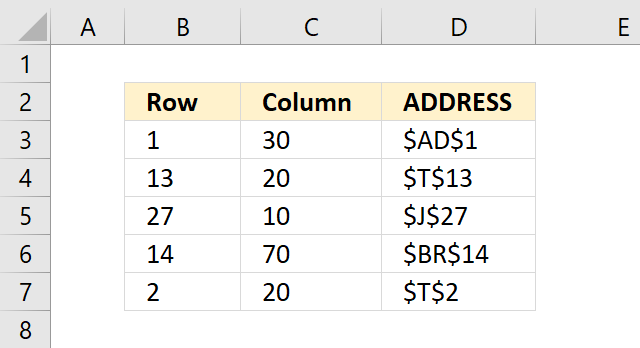
ADDRESS function returns the address of a specific cell, you need to provide a row and column number.
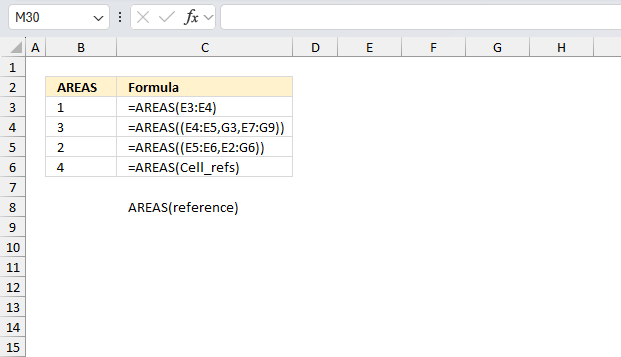
AREAS function returns the number of cell ranges and single cells in a reference.
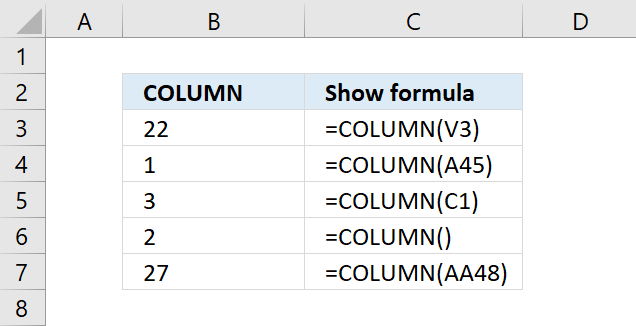
COLUMN function returns the column number of the top-left cell of a cell reference.
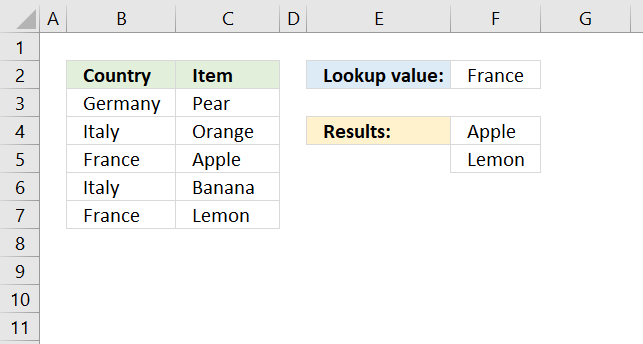
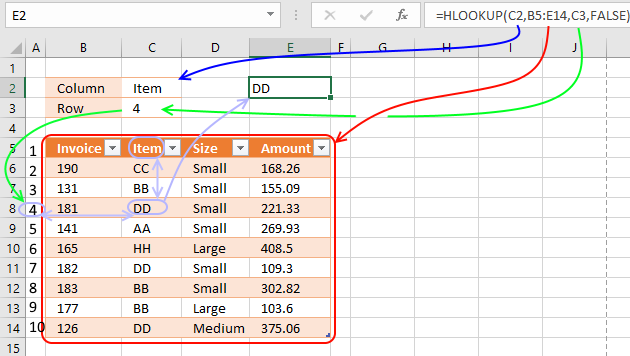
HLOOKUP function searches the top row in a data range for a value and return another value on the same column in a row you specify.
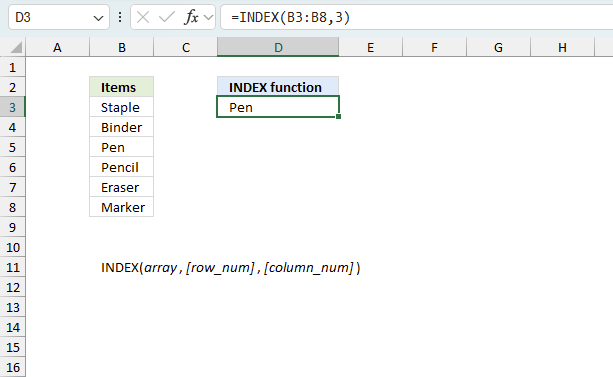
INDEX function returns a value or reference from a cell range or array, you specify which value based on a row and column number.
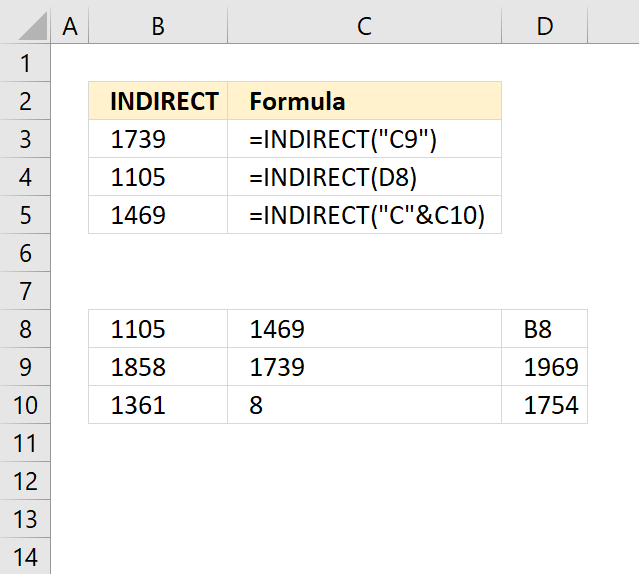
INDIRECT function returns the cell reference based on a text string and shows the content of that cell reference.
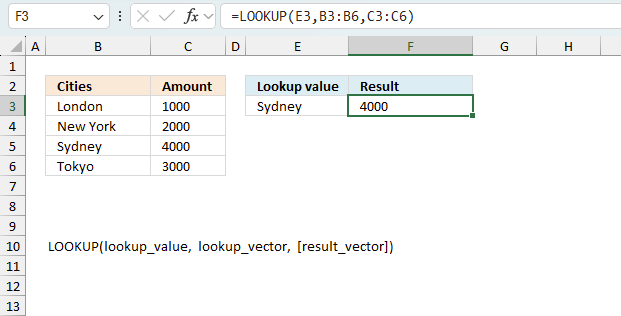
LOOKUP function find a value in a cell range and return a corresponding value on the same row.
MAKEARRAY function returns an array with a specific number of rows and columns calculated by applying a LAMBDA function.
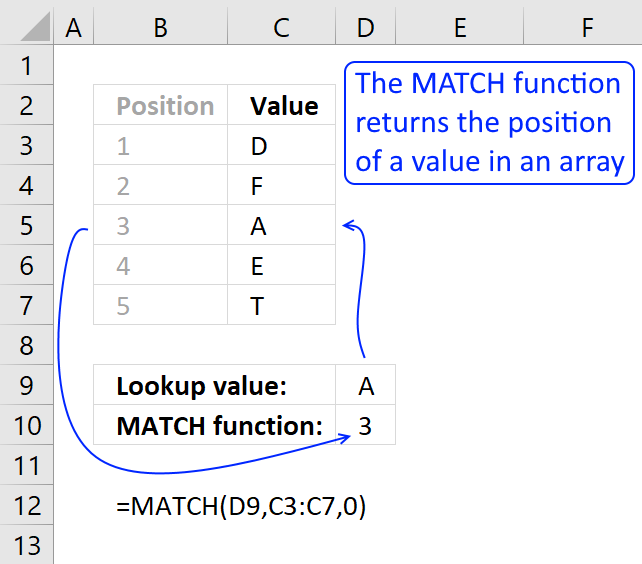
MATCH function returns the relative position of an item in an array that matches a specified value in a specific order.
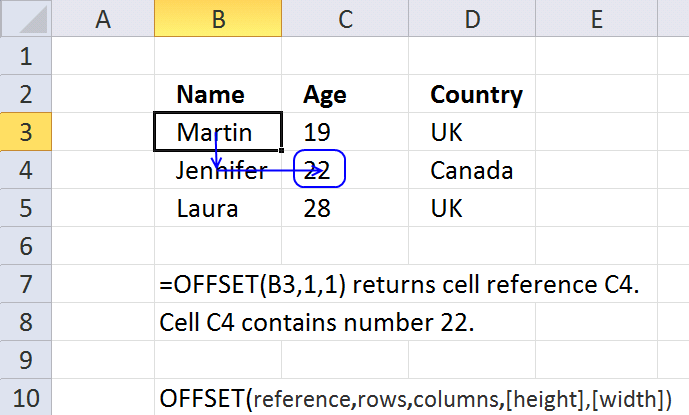
OFFSET function returns a reference to a range that is a given number of rows and columns from a given reference.
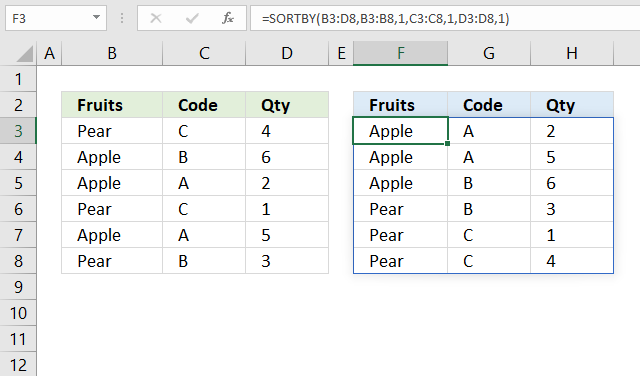
SORTBY function sorts a cell range or array based on values in a corresponding range or array.
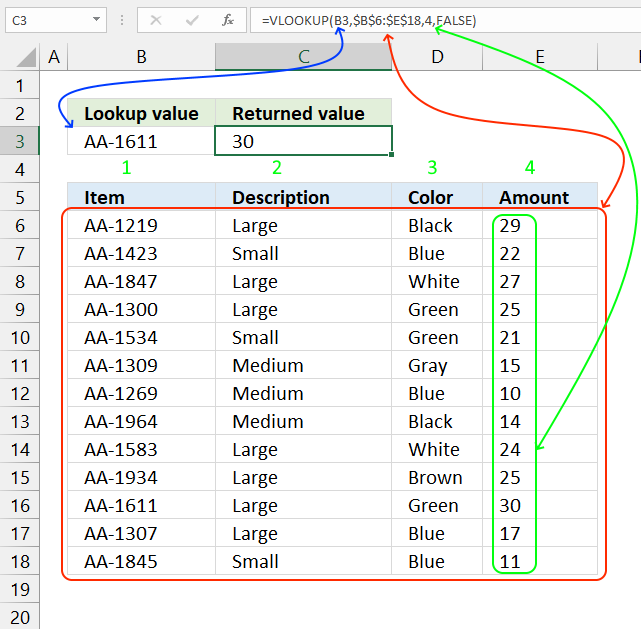
VLOOKUP function lets you search the leftmost column for a value and return another value on the same row in a column you specify.
XLOOKUP function search one column for a given value, and return a corresponding value in another column from the same row.
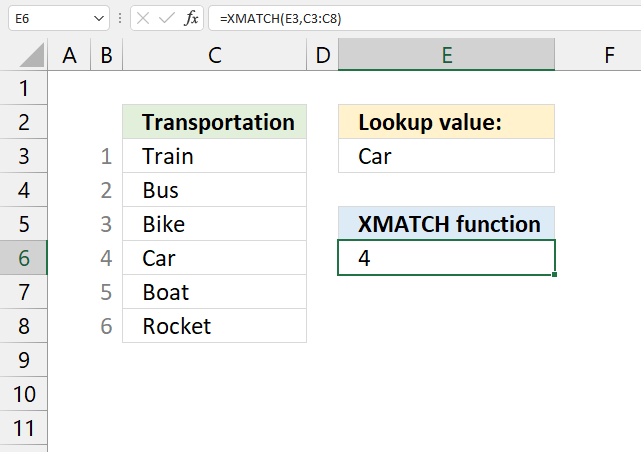
XMATCH function searches for an item in an array or cell range and returns the relative position.
Back to top
Math and trigonometry
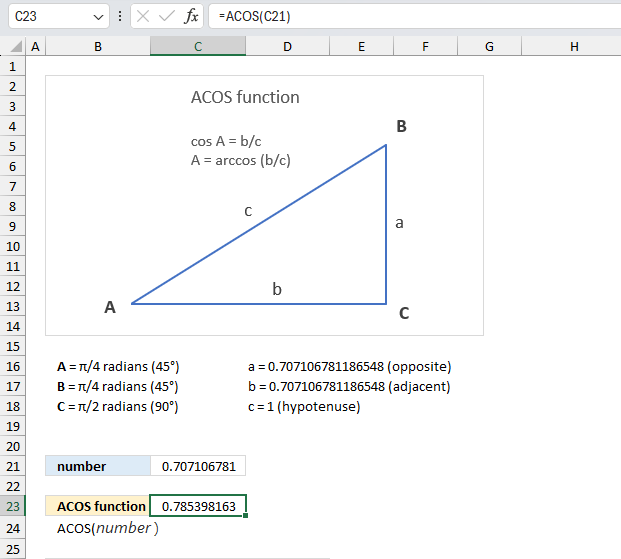
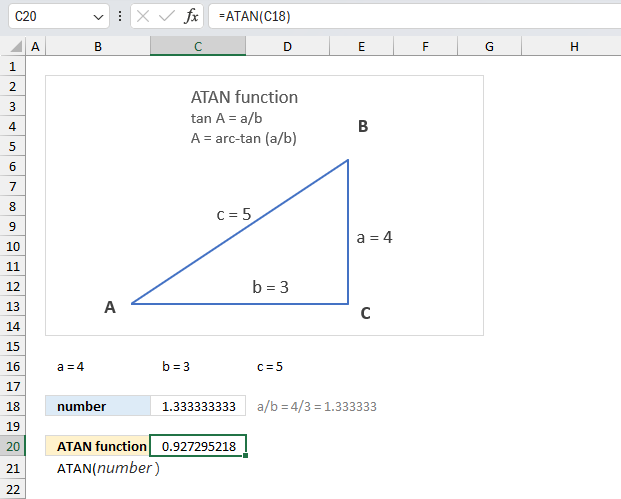
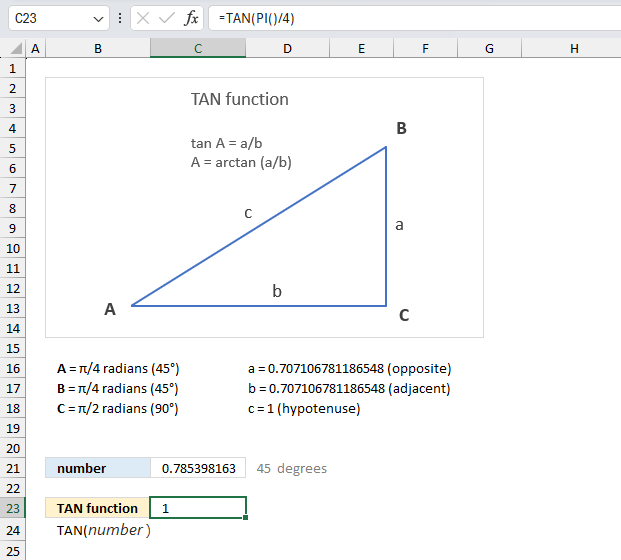
ACOS function calculates the arccosine, or inverse cosine, of a number.
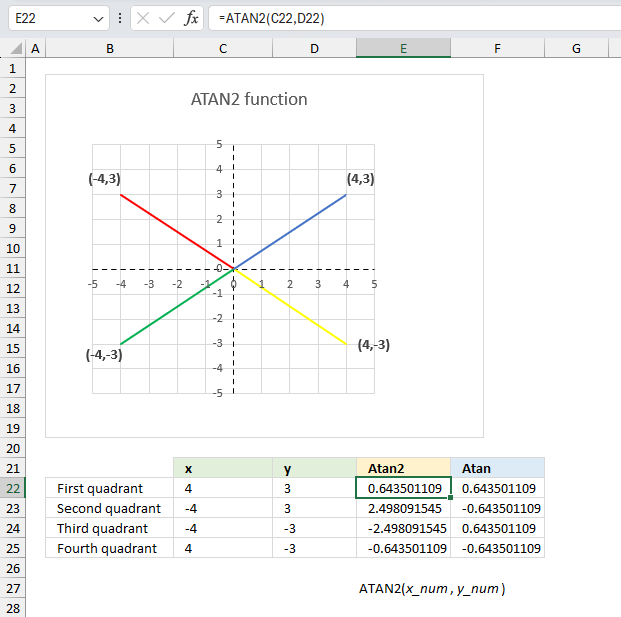
ATAN2 function calculates the arctangent of an angle using specific x- and y-coordinates.
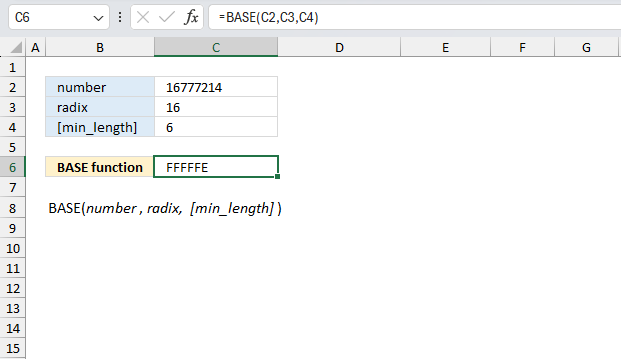
BASE function converts a number into a text representation with a given radix (base).
COMBIN function returns the number of combinations for a specific number of elements out of a larger group.
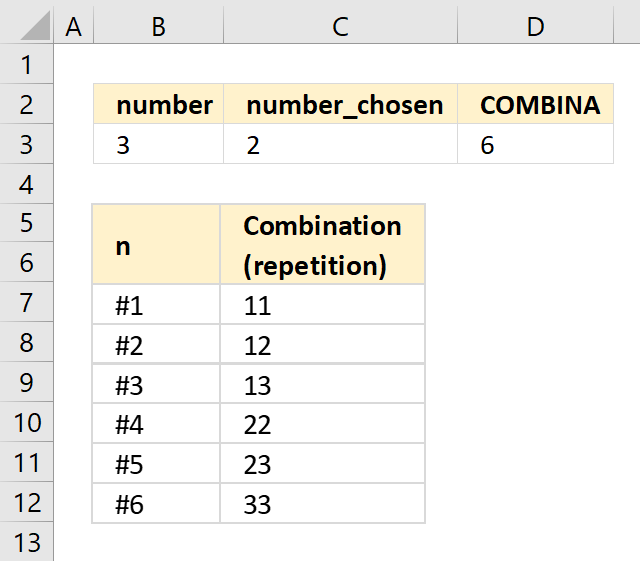
COMBINA function calculates the number of combinations for a given number of elements from a larger group of elements.
COT function calculates the cotangent of an angle specified in radians.
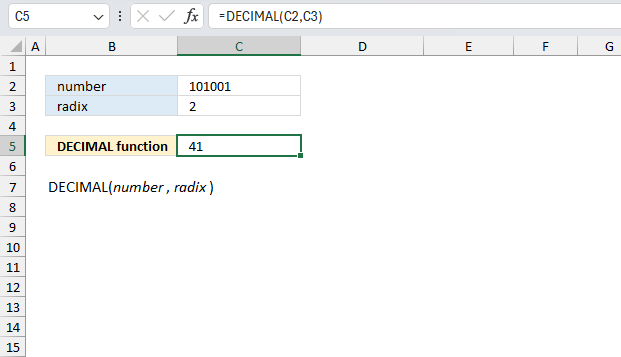
DECIMAL function converts a text representation of a number in a given base into a decimal number.
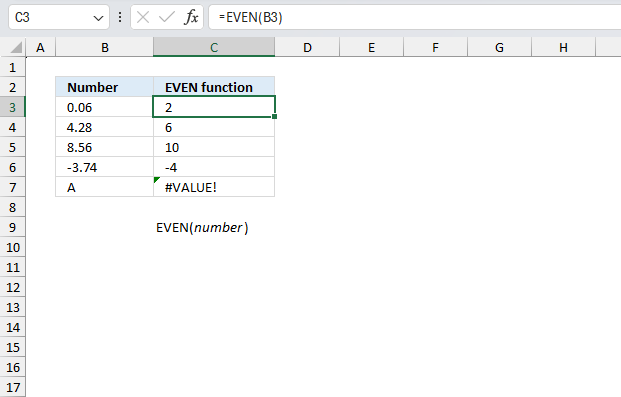
EVEN function rounds a number up to the nearest even whole number.
EXP function returns e raised to the power of a number, e equals 2.71828182845904.
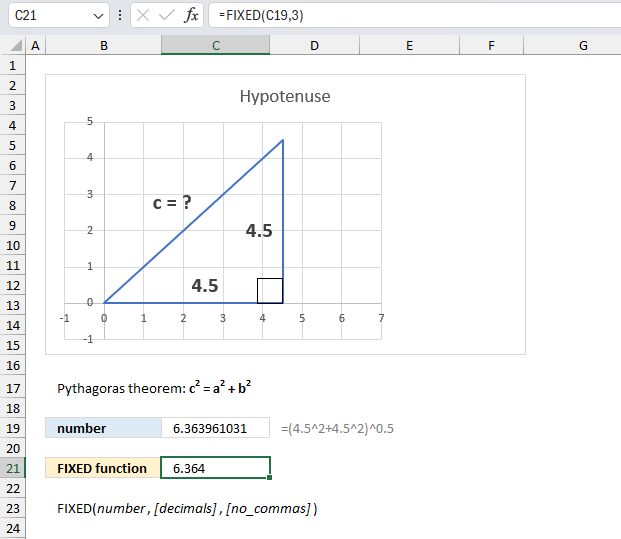
FIXED function rounds a number to the specified number of decimals, formats the number in decimal format using a period and commas, and returns the result as text.
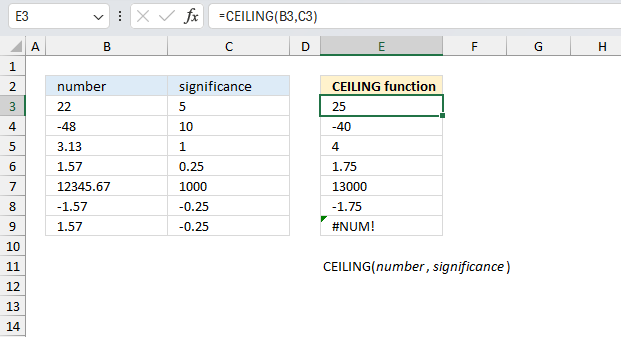
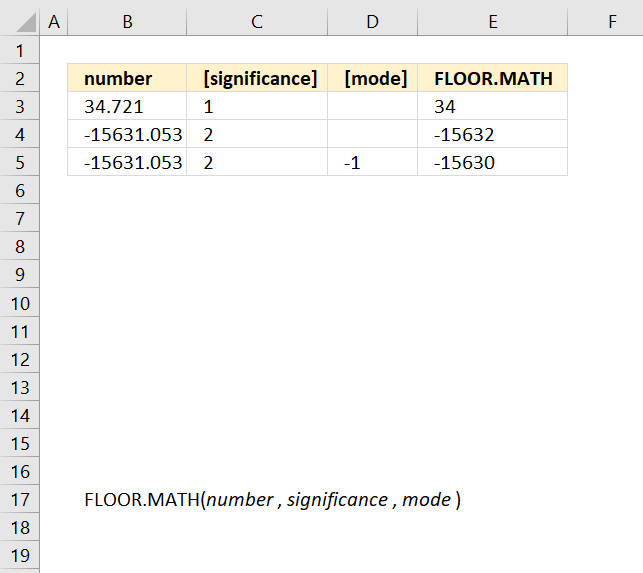
FLOOR.MATH function rounds a number down to the nearest integer or to the nearest multiple of significance.
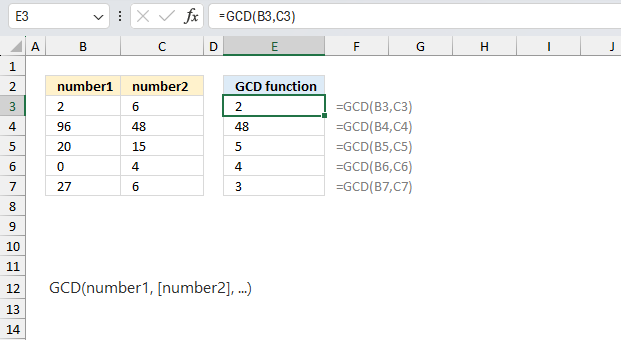
GCD function calculates the greatest common divisor that divides all given arguments without a remainder.
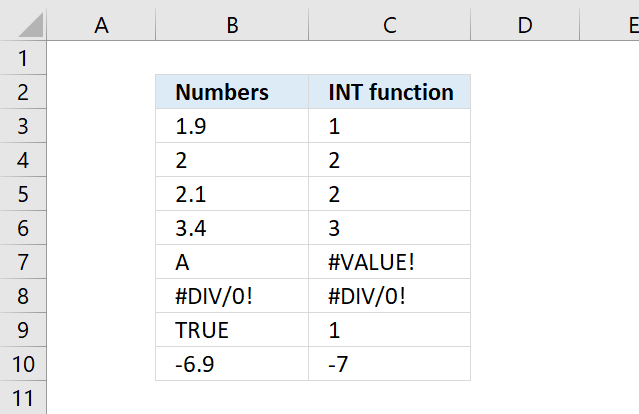
INT function removes the decimal part from positive numbers and returns the whole number (integer) except negative values are rounded down to the nearest integer.
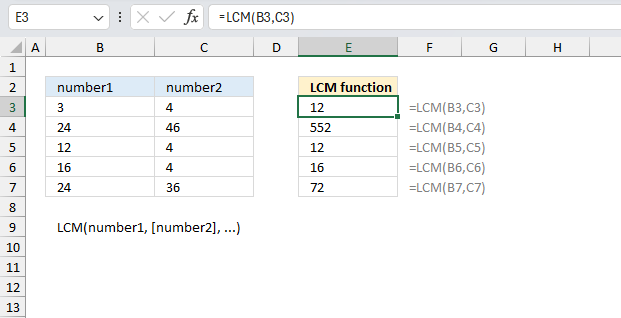
LCM function calculates the least common multiple. The least common multiple is the smallest positive integer that is a multiple of all integer arguments. Use the LCM function to find fractions with different denominators.
LET function lets you name intermediate calculation results which can shorten formulas considerably and improve performance.
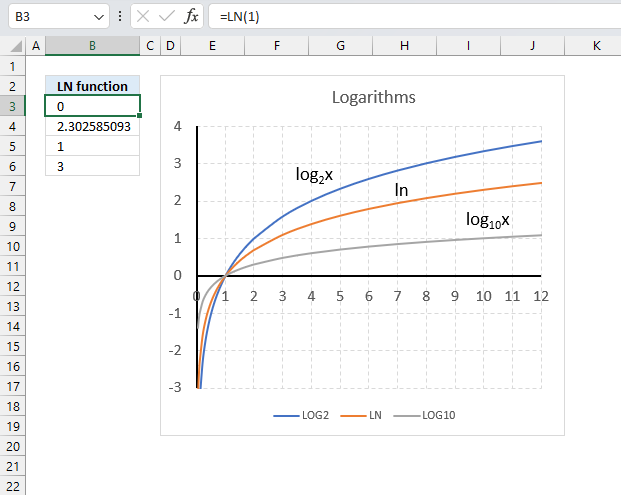
LN function calculates the natural logarithm of a number. Natural logarithms are based on the constant e.
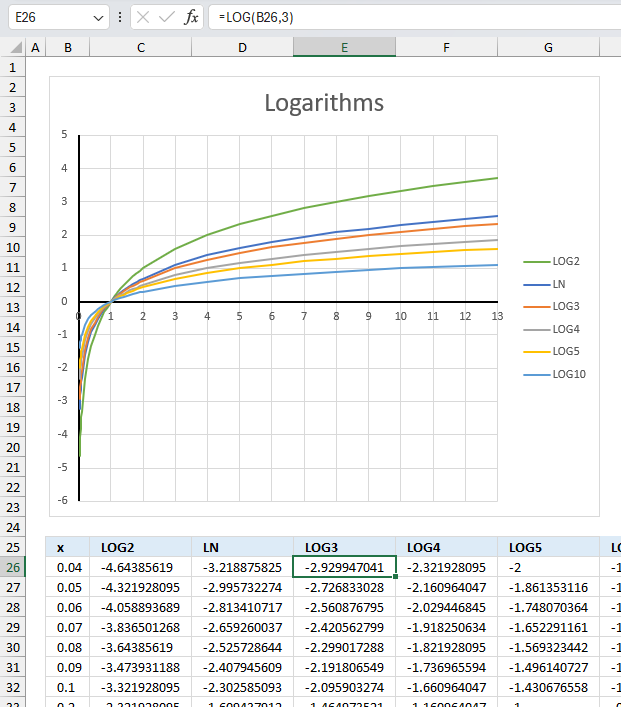
LOG function calculates the logarithm of a number to a specific base.
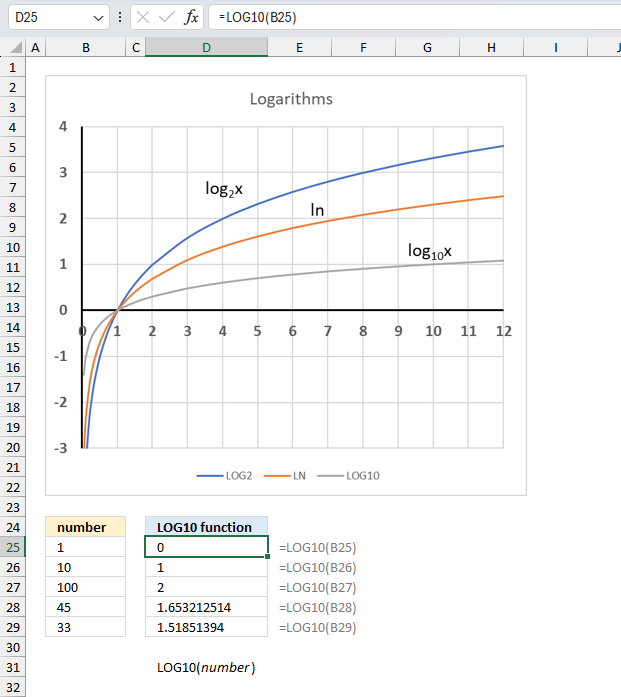
LOG10 function calculates the logarithm of a number using the base 10.
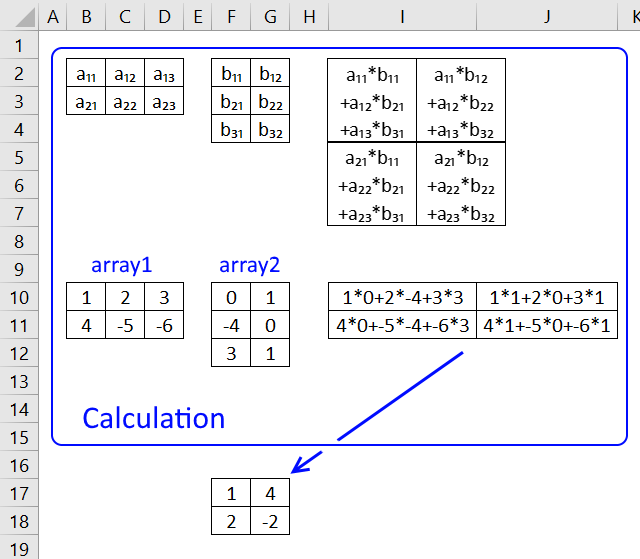
MMULT function calculates the matrix product of two arrays, an array as the same number of rows as array1 and columns as array2.
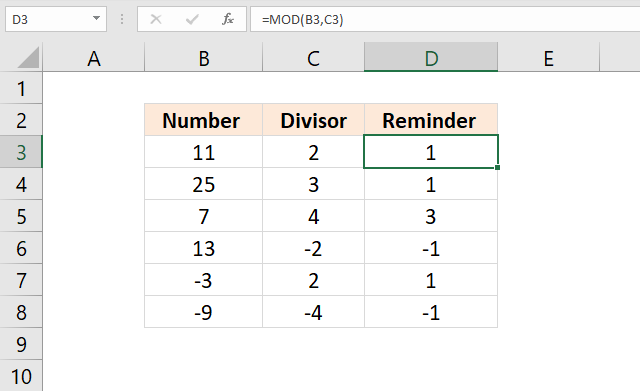
MOD function returns the remainder after a number is divided by divisor.
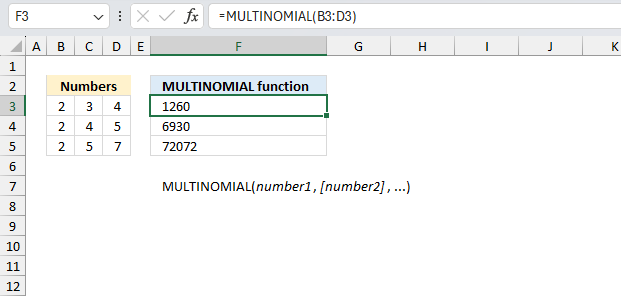
MULTINOMIAL function calculates the ratio of the factorial of a sum of values to the product of factorials.
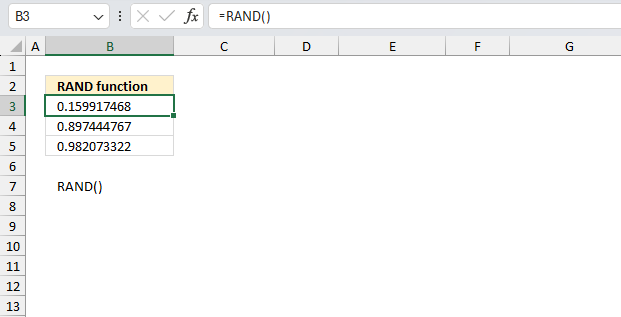
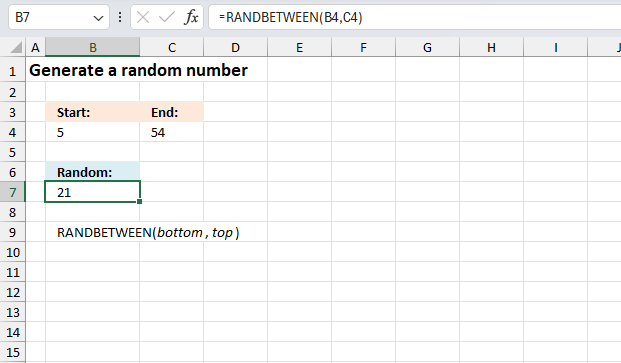
RAND function calculates a random real number greater than or equal to 0 and less than 1.
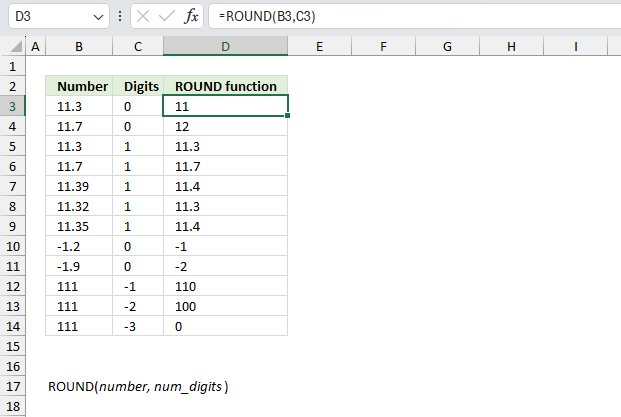
ROUND function rounds a number based on the number of digits you specify.
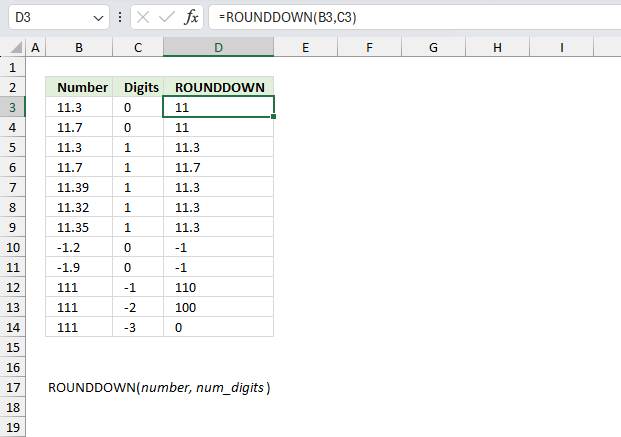
ROUNDDOWN function rounds a number down based on the number of digits to which you want to round the number.
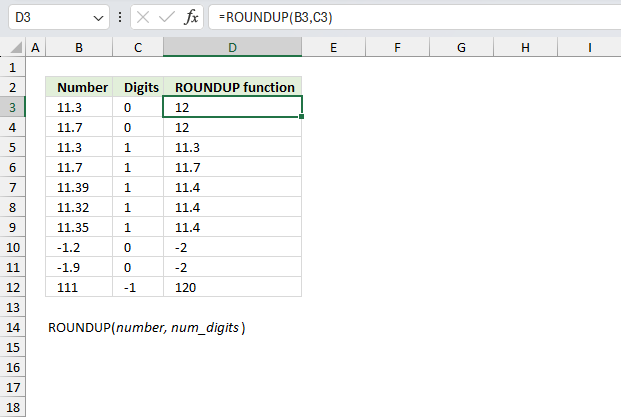
ROUNDUP function calculates a number rounded up based on the number of digits to which you want to round the number.
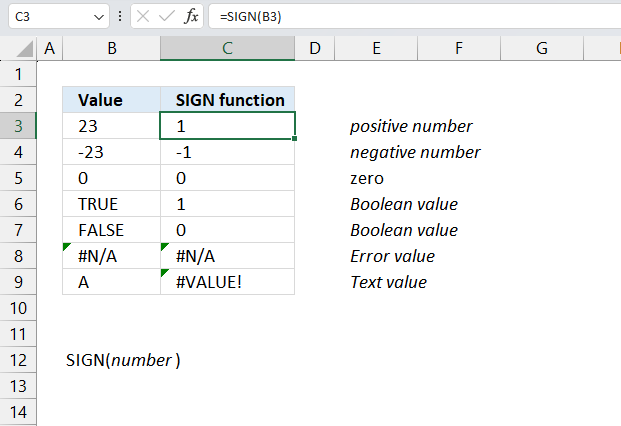
SIGN function returns the sign of a number. 1 for a positiv number, 0 (zero) for a 0 (zero) and -1 for a negative number.
SUBTOTAL function returns a subtotal from a list or database, you can choose from a variety of arguments that determine what you want the function to do.
SUM function allows you to add numerical values, the function returns the sum in the cell it is entered in. The SUM function is cleverly designed to ignore text and boolean values, adding only numbers.
SUMPRODUCT function calculates the product of corresponding values and then returns the sum of each multiplication.
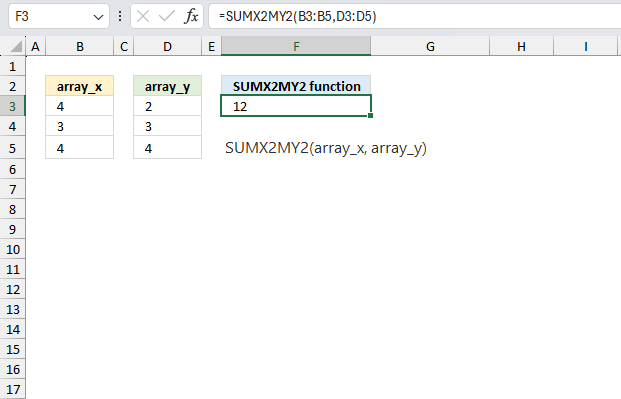
SUMX2MY2 function calculates the sum of the difference of squares of corresponding values in two arrays.
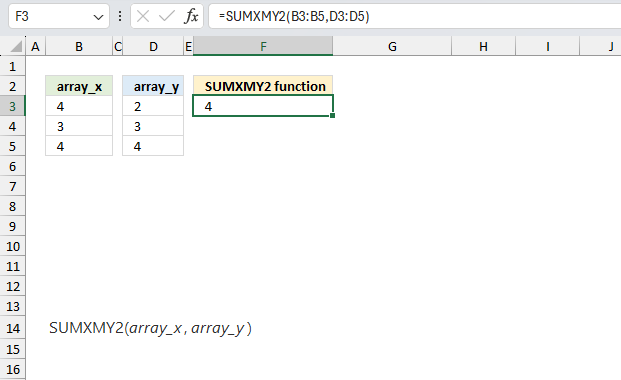
SUMXMY2 function calculates the sum of squares of differences of corresponding values in two arrays.
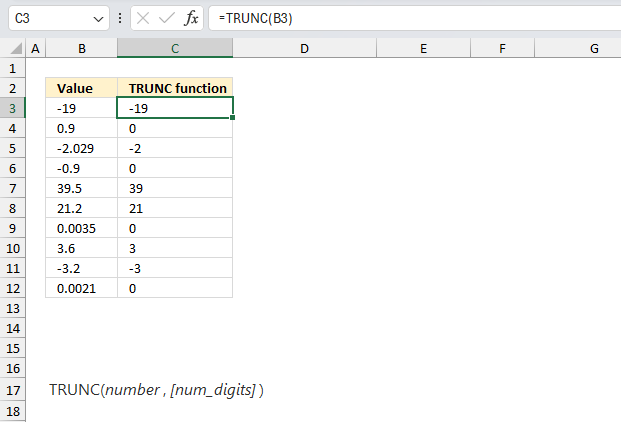
TRUNC function removes the fractional part of the number to an integer.
Back to top
Statistical
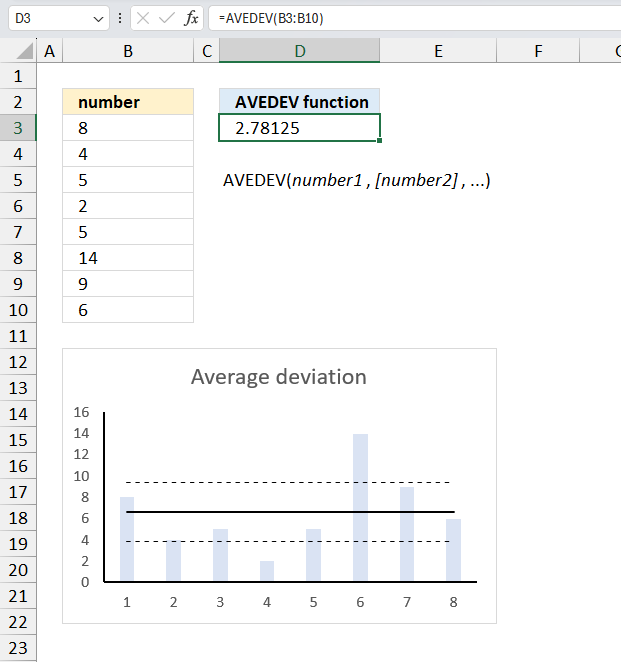
AVEDEV function calculates the average of the absolute deviations of data points from their mean.
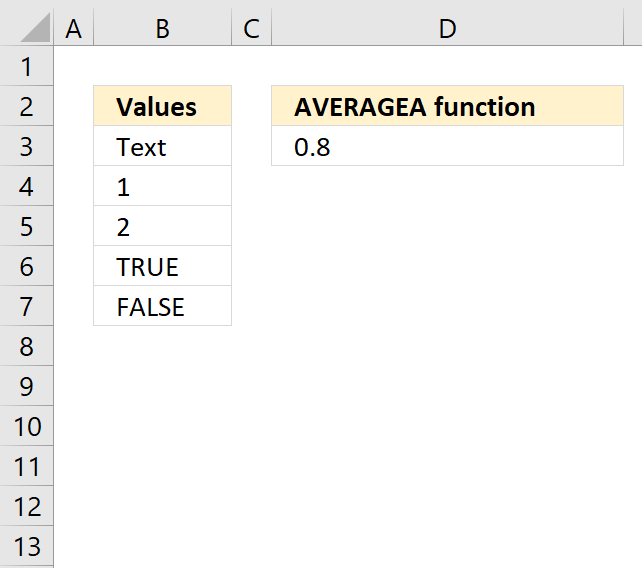
AVERAGEA function returns the average of a group of values. Text and boolean value FALSE evaluates to 0. TRUE to 1.
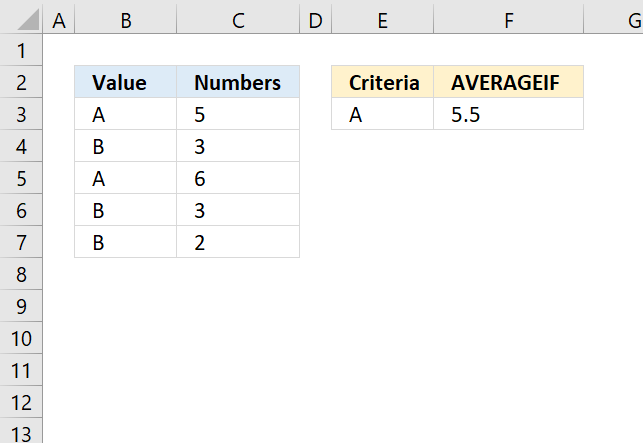
AVERAGEIF function returns the average of cell values that are valid for a given condition.
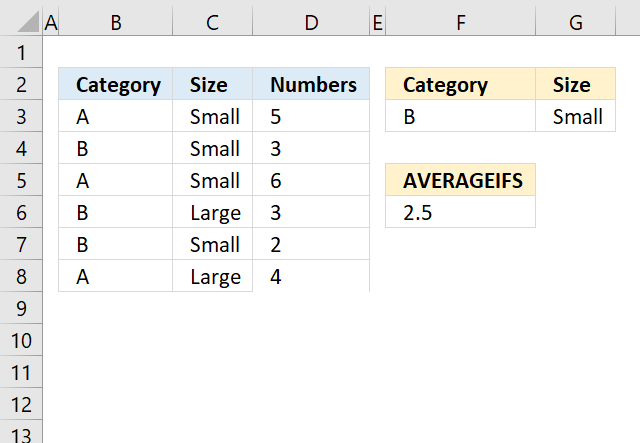
AVERAGEIFS function returns the average of cell values that evaluates to TRUE for multiple criteria.
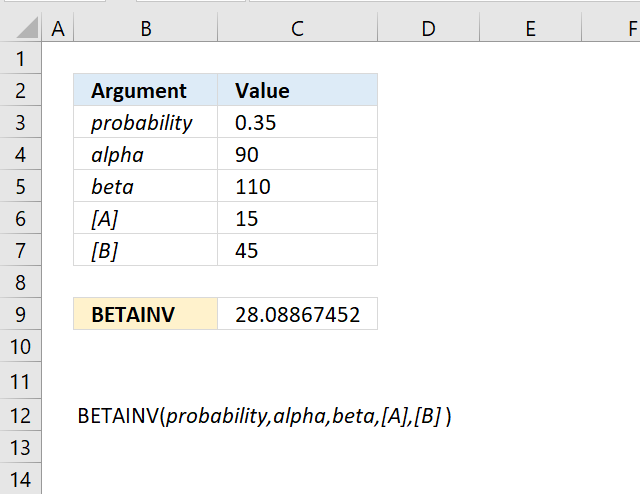
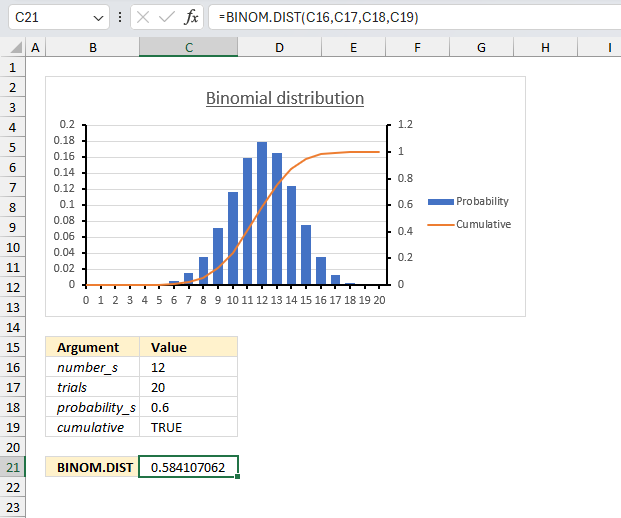
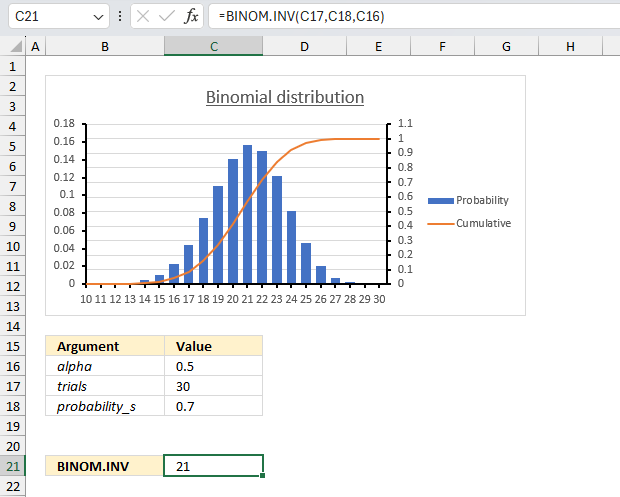
BINOM.INV function calculates the minimum value for which the binomial distribution is equal to or greater than a given threshold value.
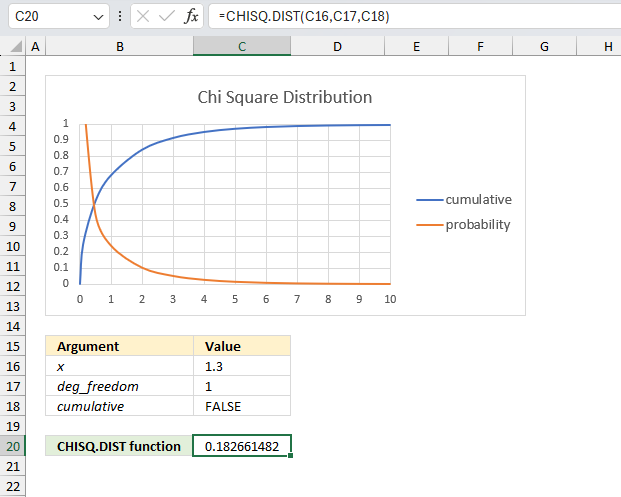
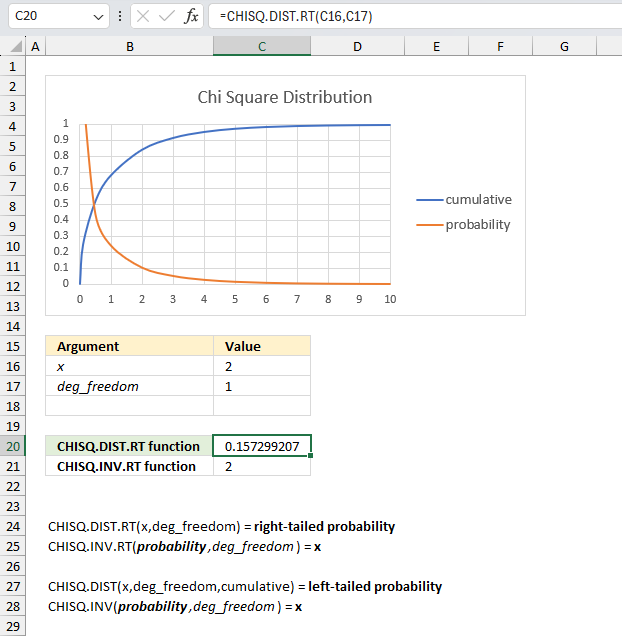
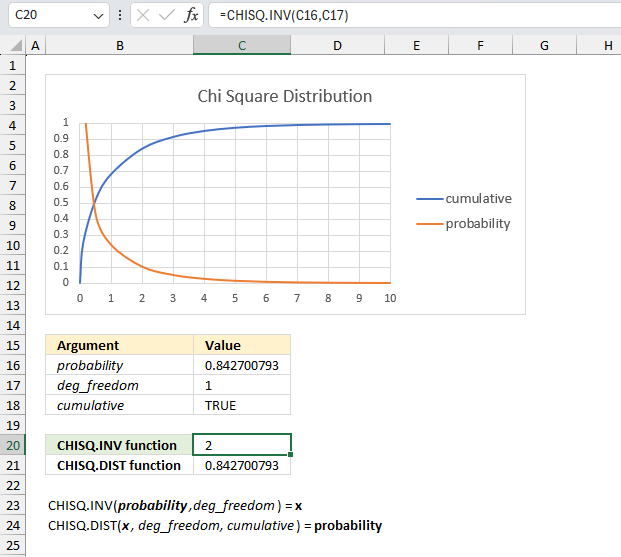
CHISQ.DIST function calculates the probability of the chi-squared distribution, cumulative distribution or probability density.
CHISQ.INV function calculates the inverse of the left-tailed probability of the chi-squared distribution.
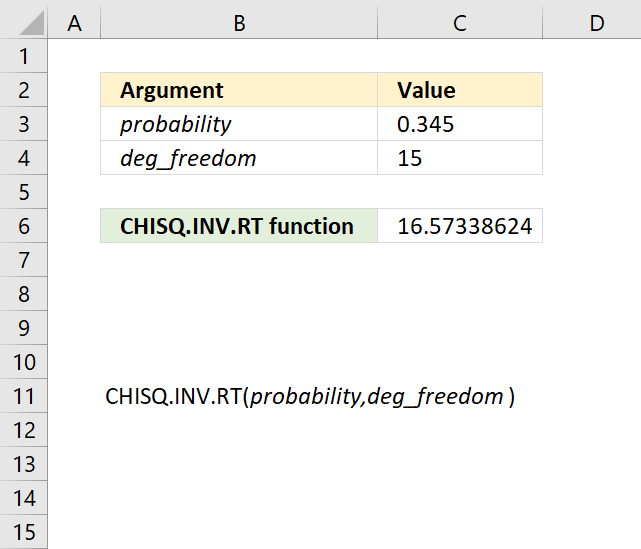
CHISQ.INV.RT function calculates the inverse of the right-tailed probability of the chi-squared distribution.
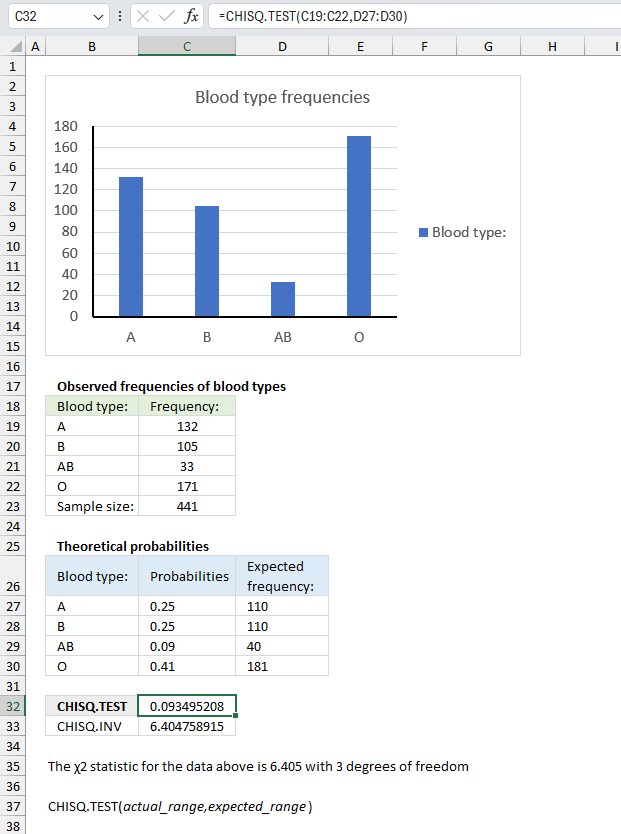
CHISQ.TEST function calculates the test for independence, the value returned from the chi-squared statistical distribution and the correct degrees of freedom. Use this function to check if hypothesized results are valid.
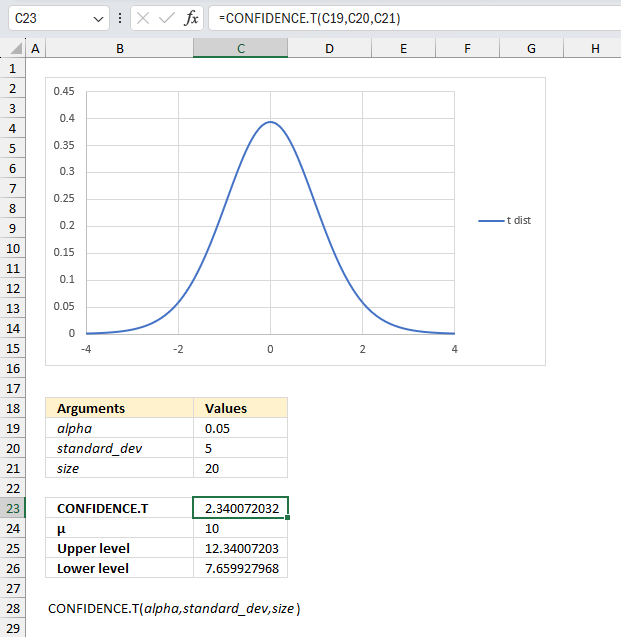
CONFIDENCE.T function calculates the confidence range for a population mean using a Student's t distribution.
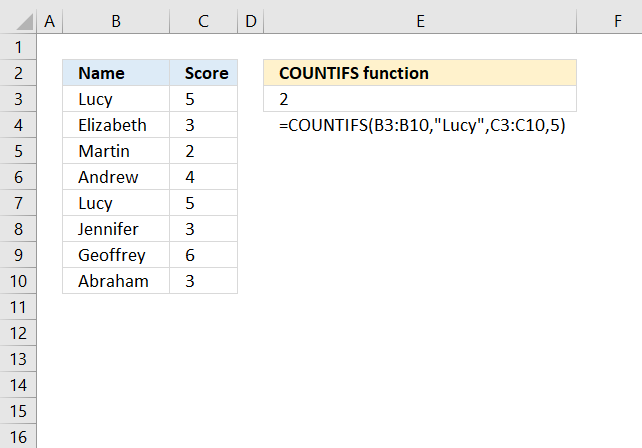
COUNTIFS function calculates the number of cells across multiple ranges that equals all given conditions.
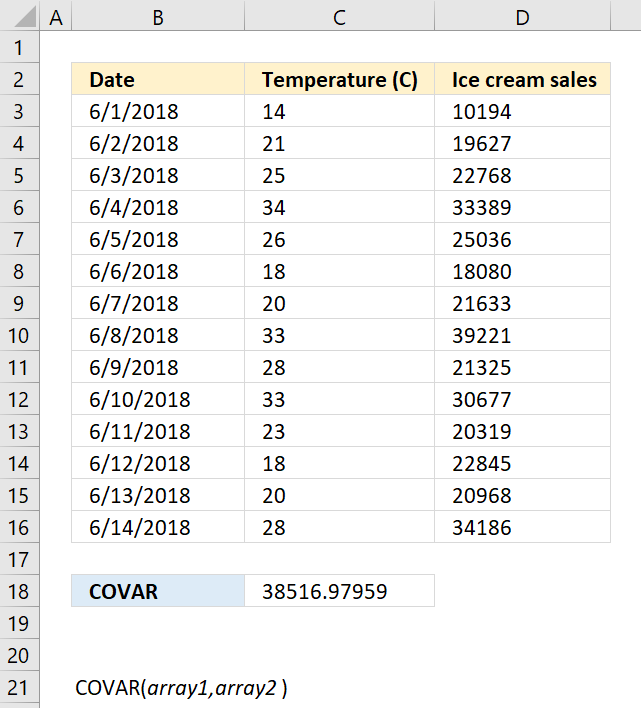
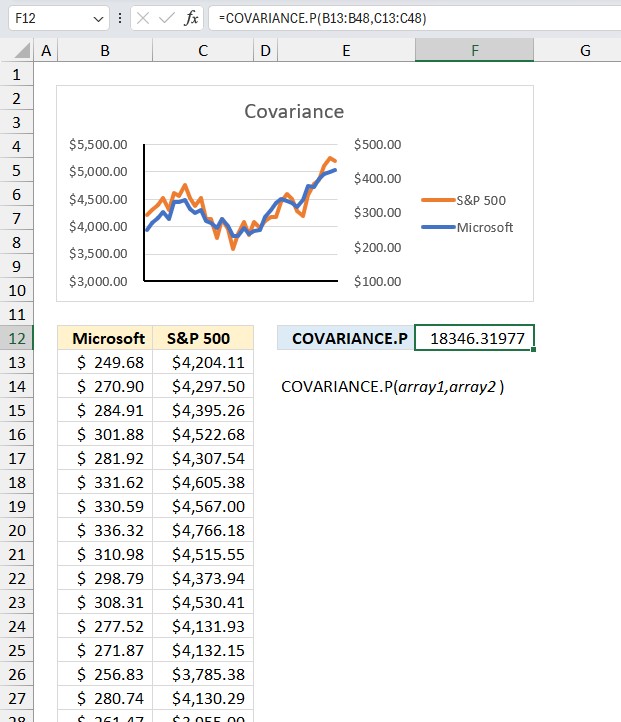
COVARIANCE.P function calculates the covariance meaning the average of the products of deviations for each pair in two different datasets.
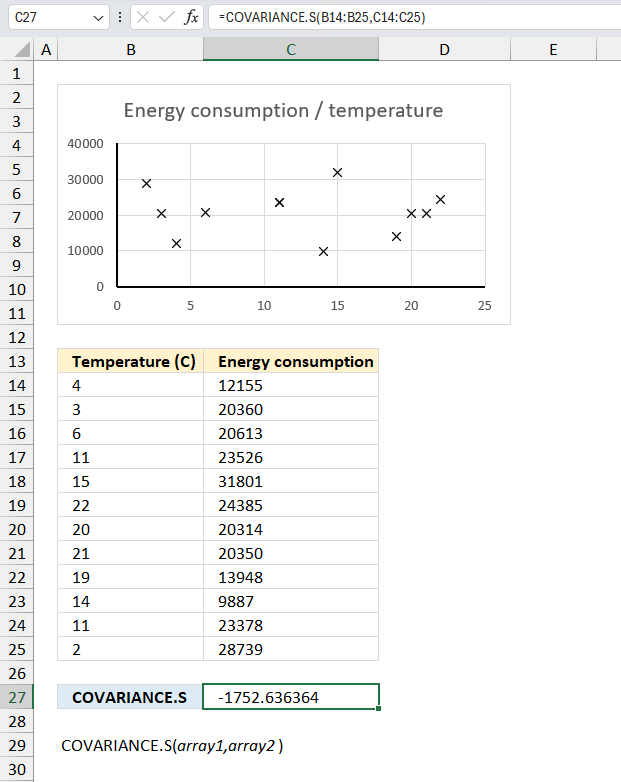
COVARIANCE.S function calculates the sample covariance meaning the average of the products of deviations for each pair in two different datasets.
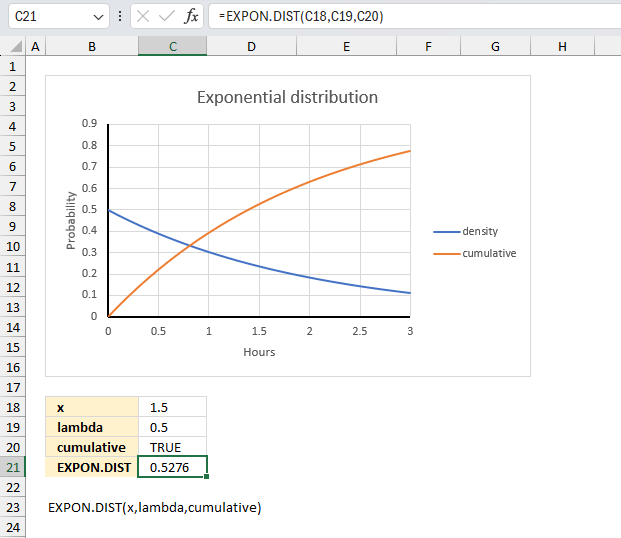
EXPON.DIST function calculates the exponential distribution representing an outcome in the form of probability.
FREQUENCY function calculates how often values occur within a range of values and then returns a vertical array of numbers.
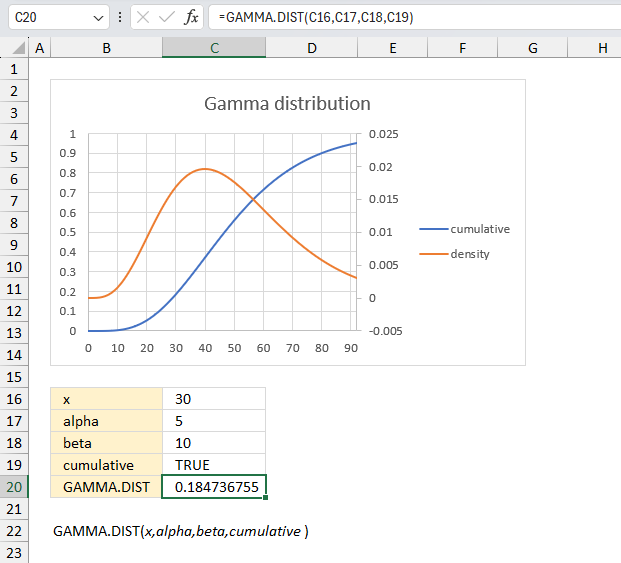
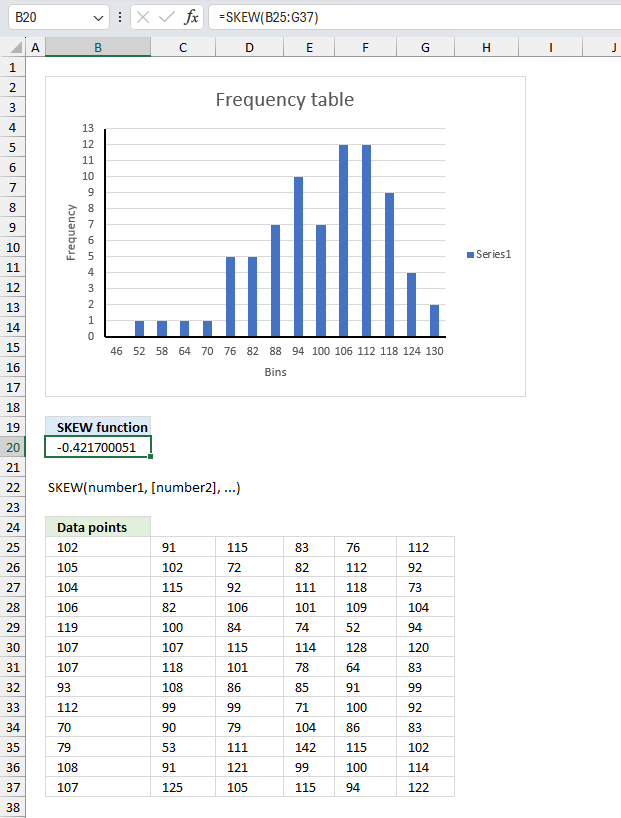
GAMMA.DIST function calculates the gamma often used in queuing analysis (probability statistics) that may have a skewed distribution.
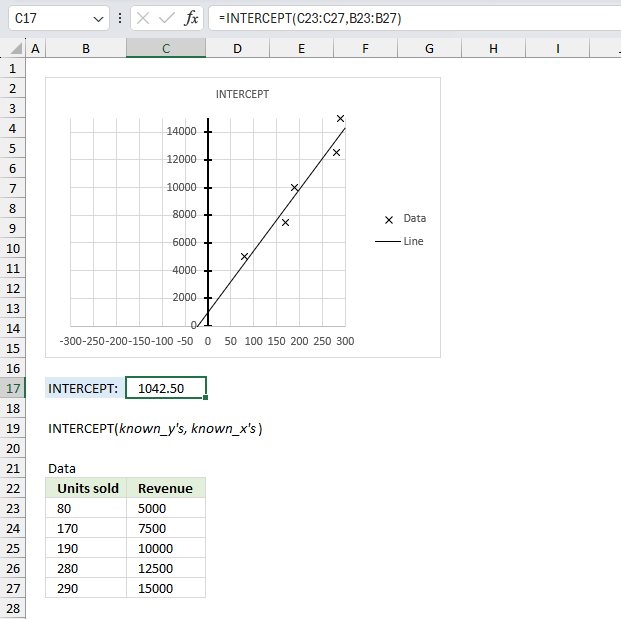
INTERCEPT function returns a value representing the y-value where a line intersects the y-axis.
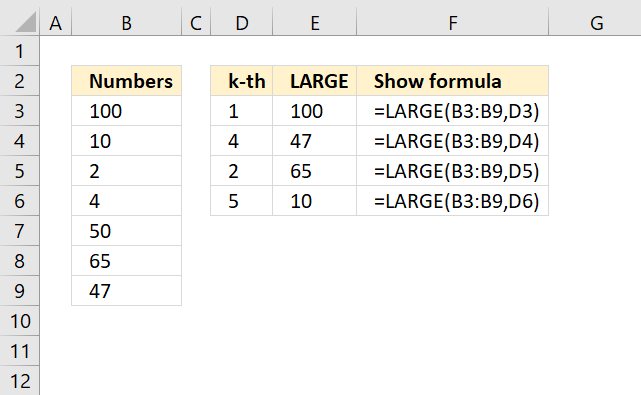
LARGE function calculates the k-th largest value from an array of numbers.
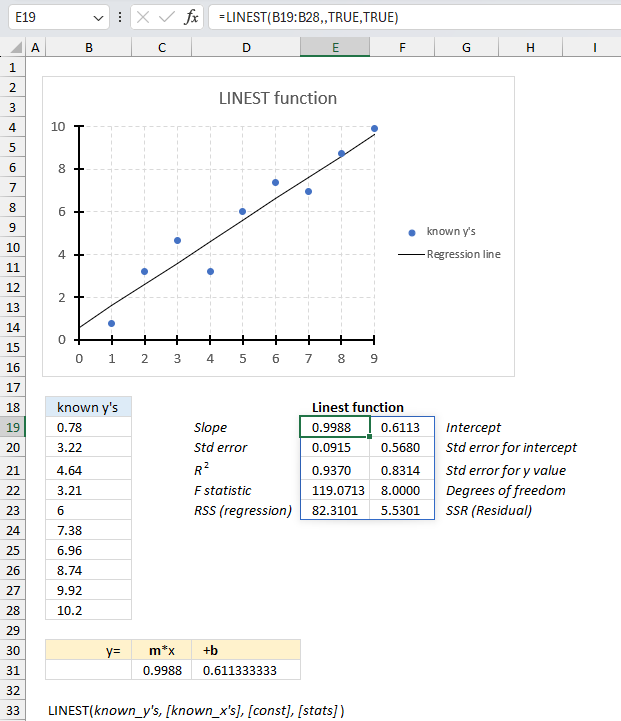
LINEST function returns an array of values representing the parameters of a straight line based on the "least squares" method.
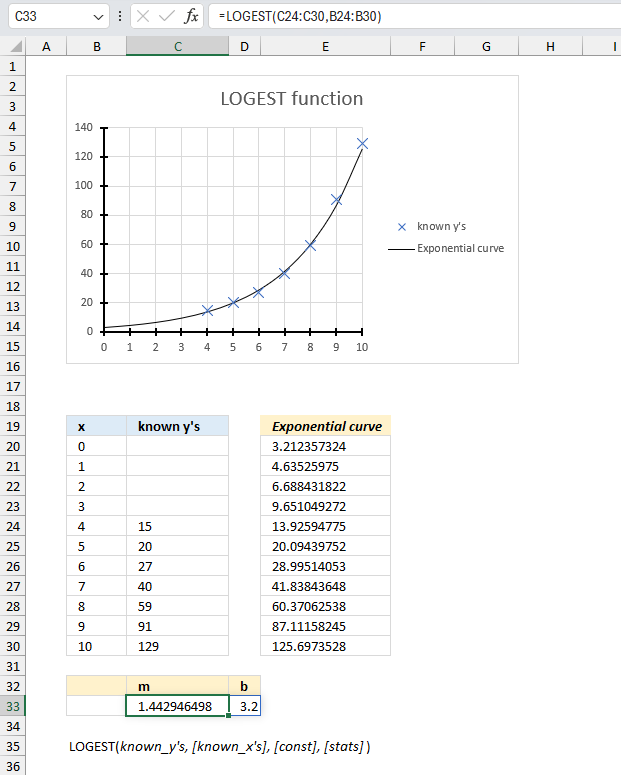
LOGEST function returns an array of values representing the parameters of an exponential curve that fits your data, based on the "least squares" method.
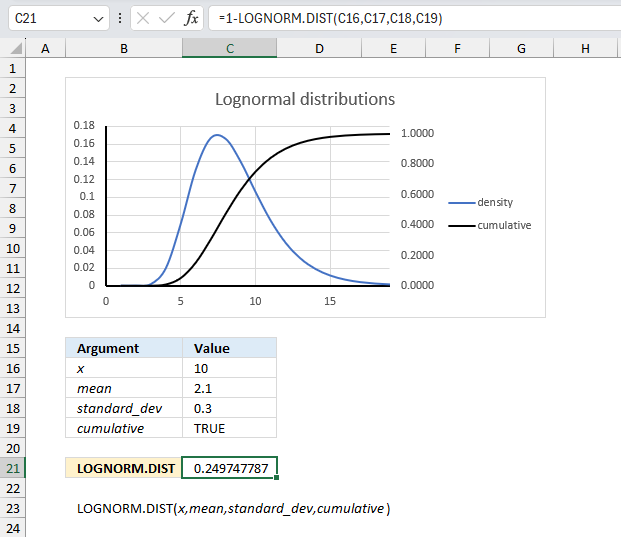
LOGNORM.DIST function calculates the lognormal distribution of argument x, based on a normally distributed ln(x) with the arguments of mean and standard_dev.
MAXIFS function calculates the highest value based on a condition or criteria.
MEDIAN function calculates the median based on a group of numbers. The median is the middle number of a group of numbers.
MINA function returns the smallest number. Text values and blanks are ignored, boolean value TRUE evaluates to 1 and FALSE to 0 (zero).
MINIFS function calculates the smallest value based on a given set of criteria.
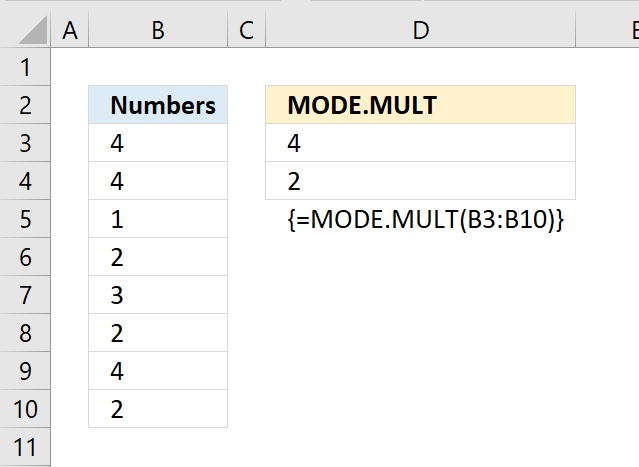
MODE.MULT function returns the most frequent number in a cell range. It will return multiple numbers if they are equally frequent.
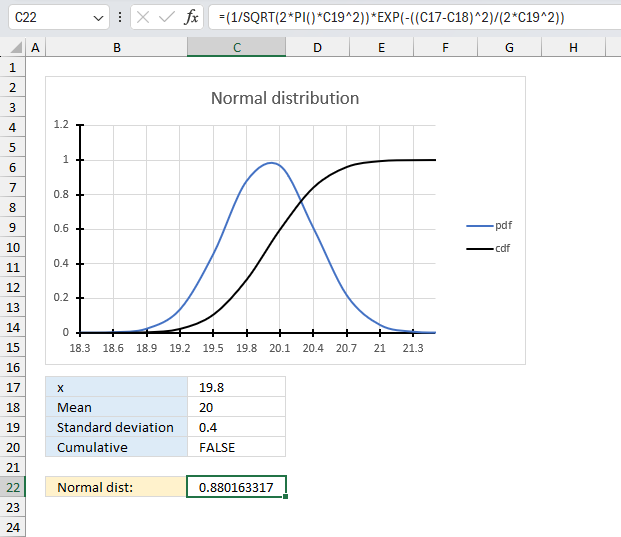
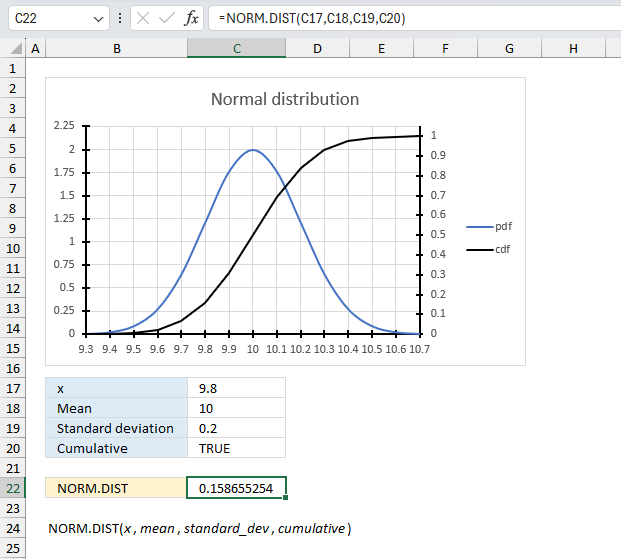
NORM.DIST function calculates the normal distribution for a given mean and standard deviation.
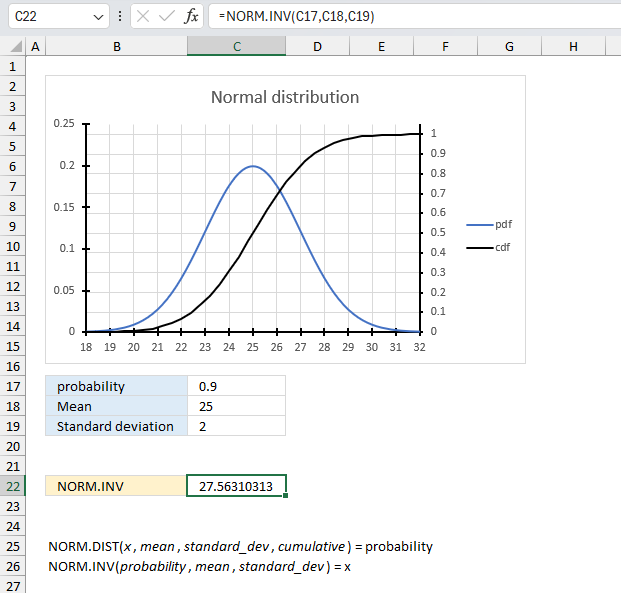
NORM.INV function calculates the inverse of the normal cumulative distribution for a given mean and standard deviation.
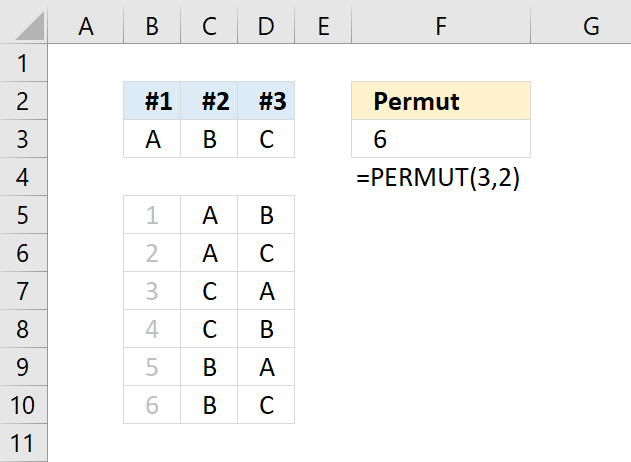
PERMUT function returns the number of permutations for a set of elements that can be selected from a larger number of elements.
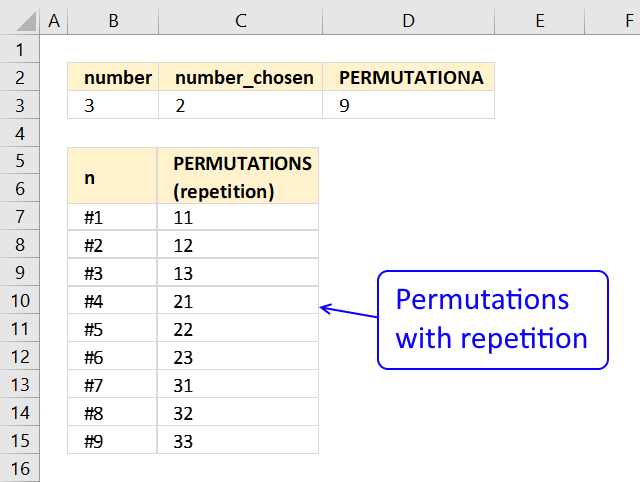
PERMUTATIONA function returns the number of permutations for a specific number of elements that can be selected from a larger group of elements.
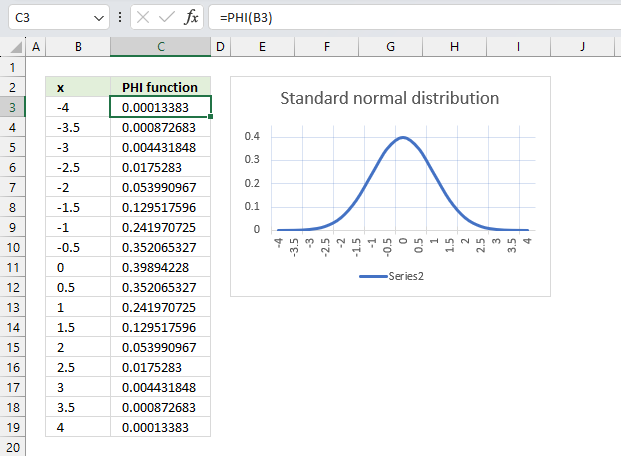
PHI function calculates a number of the density function for a standard normal distribution.
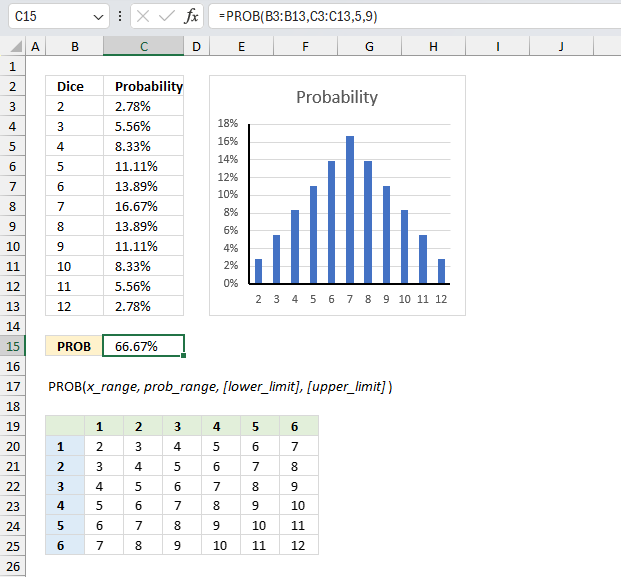
PROB function calculates the probability that values in a range are between a given lower and upper limit.
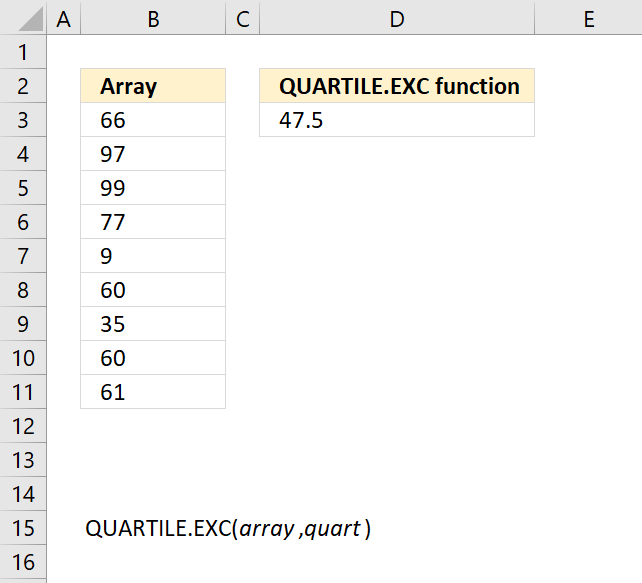
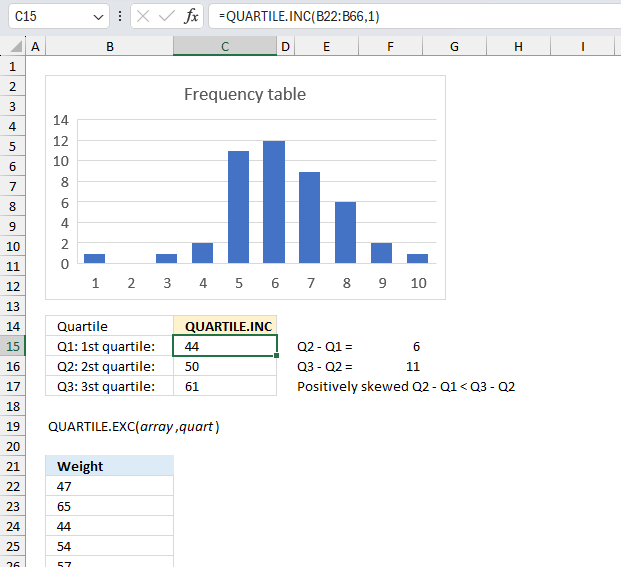
QUARTILE.INC function returns the quartile of a data set, based on percentile values from 0..1, inclusive.
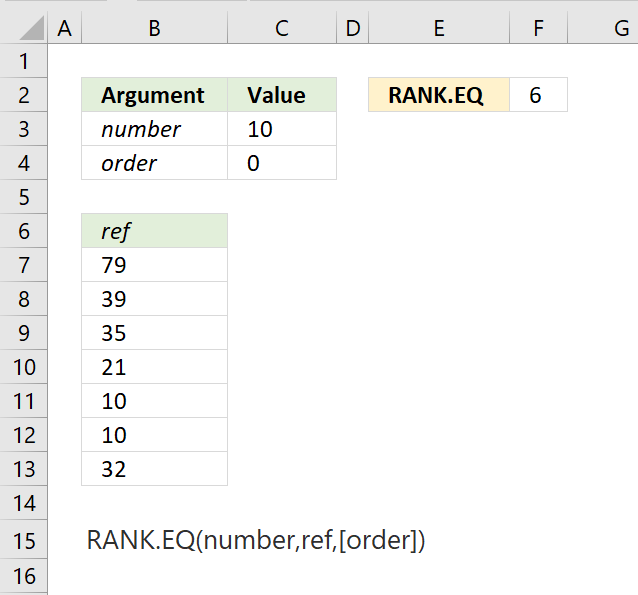
RANK.EQ function calculates the rank of a number in a list of numbers, based on its position if the list were sorted.
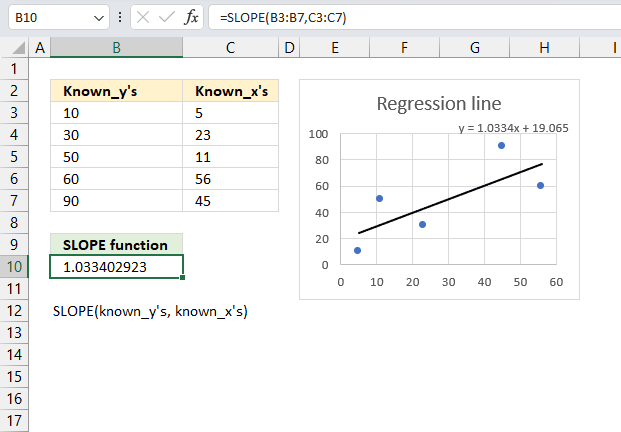
SLOPE function calculates the slope of the linear regression line through coordinates.
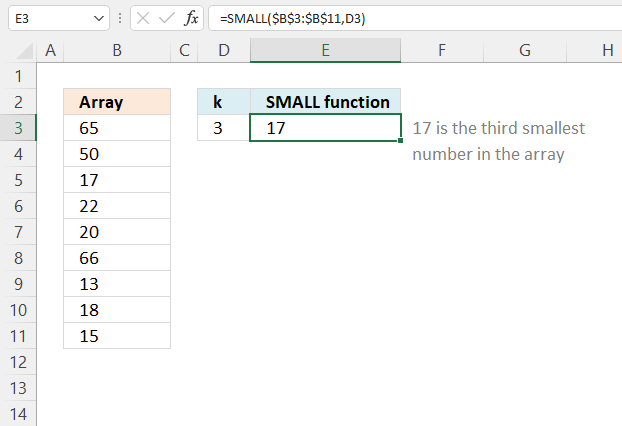
SMALL function returns the k-th smallest value from a group of numbers.
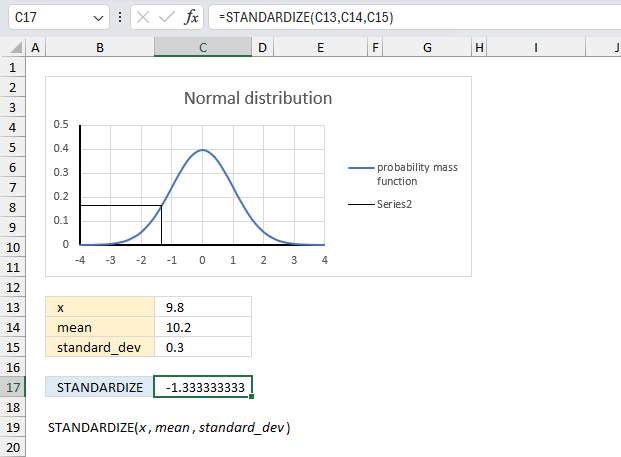
STANDARDIZE function calculates a normalized value from a distribution characterized by mean and standard_dev.
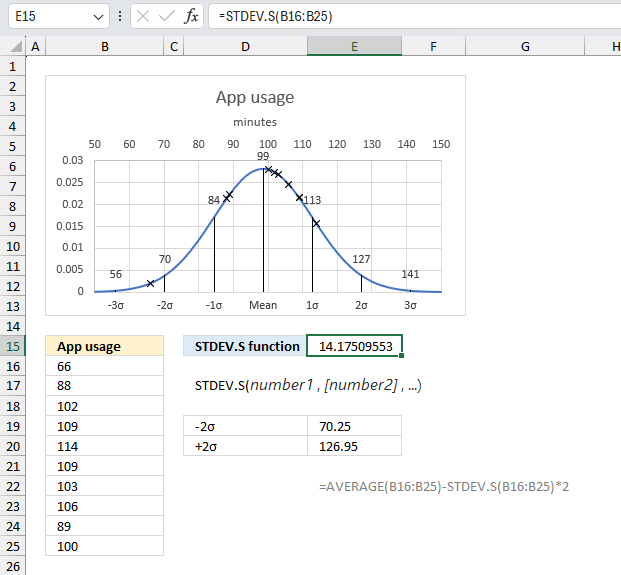
STDEV.S function returns standard deviation based on a sample of the entire population.
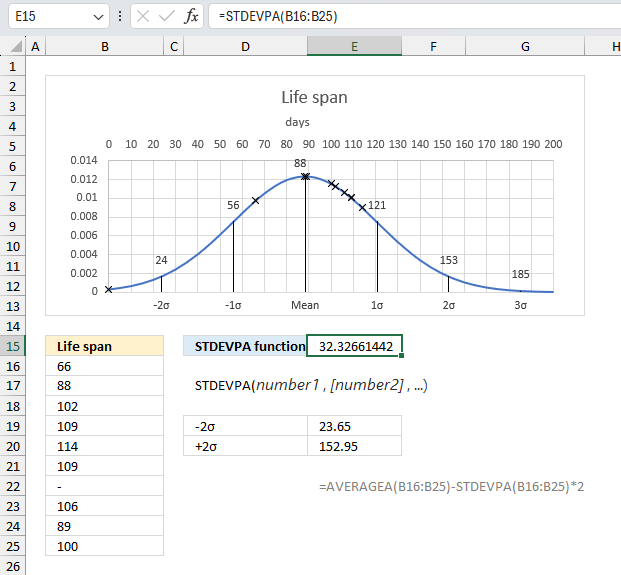
STDEVPA function returns the standard deviation based on the entire population, including text and logical values.
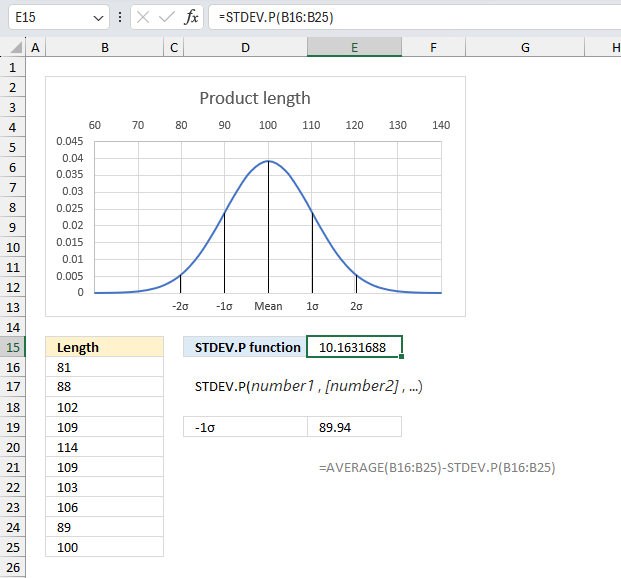
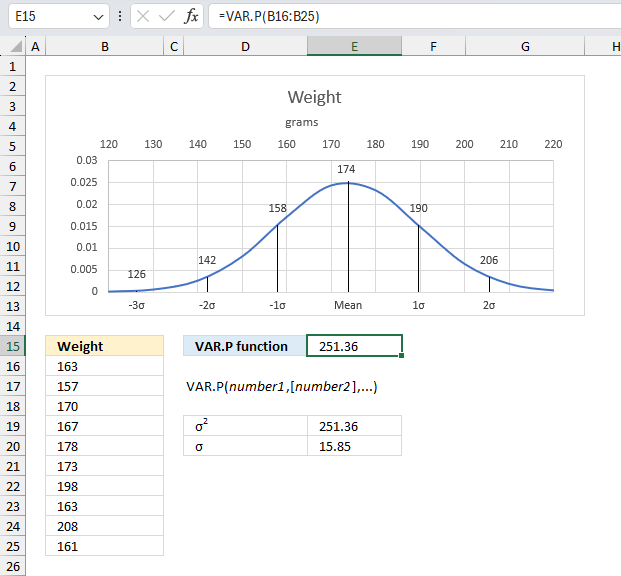
VAR.P function returns the variance based on the entire population. The function ignores logical and text values.
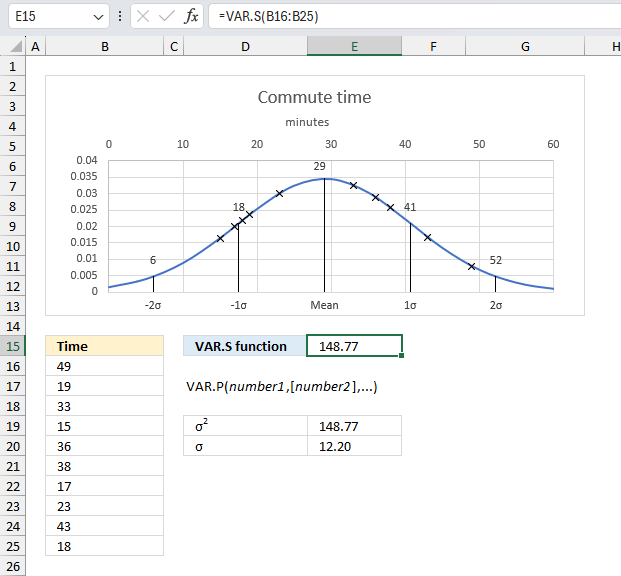
VAR.S function the VAR.S function tries to estimate the variance based on a sample of the population. The function ignores logical and text values.
Back to top
Text
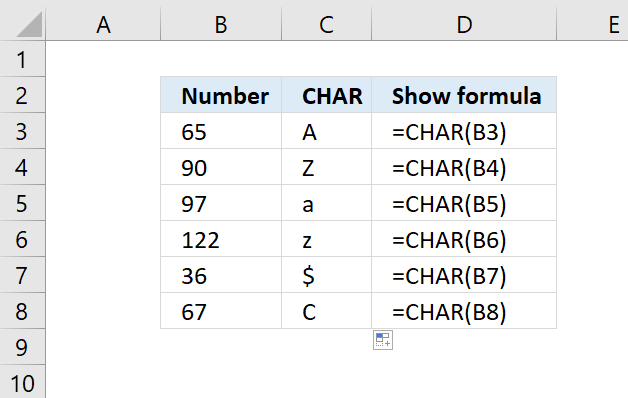
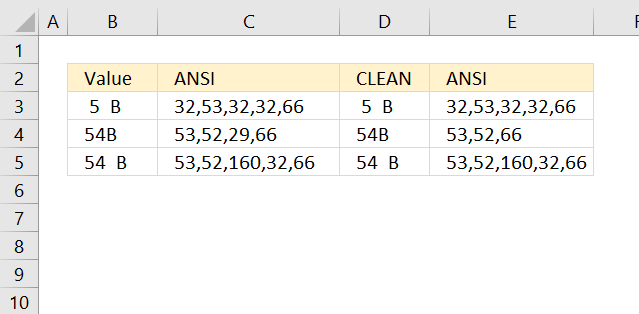
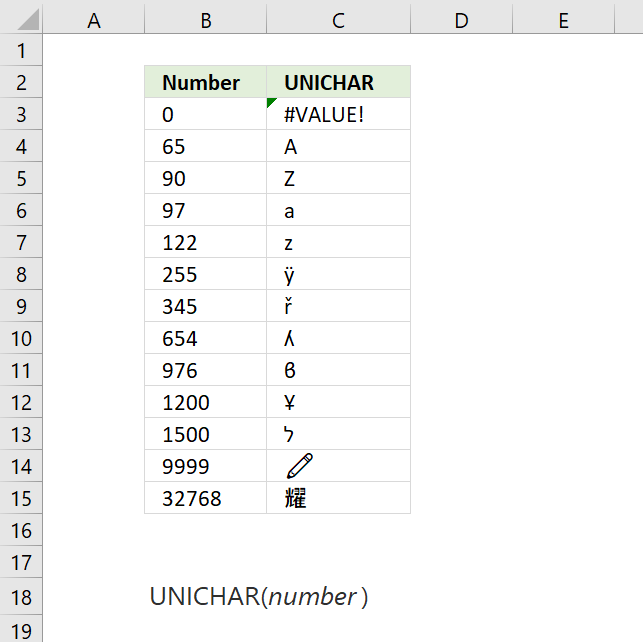
CHAR function converts a number to the corresponding ANSI character determined by your computers character set.
CLEAN function deletes the first 32 nonprinting characters in 7-bit ASCII code in your argument.
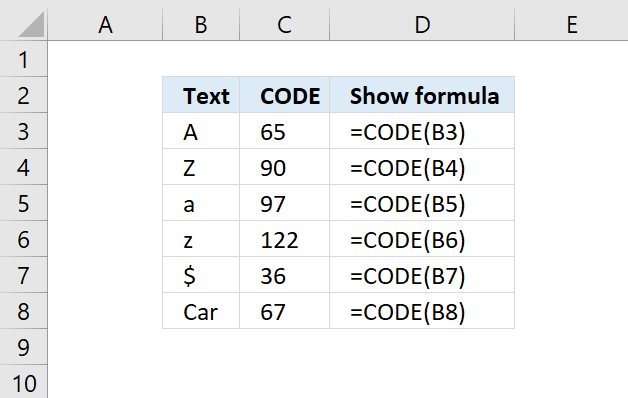
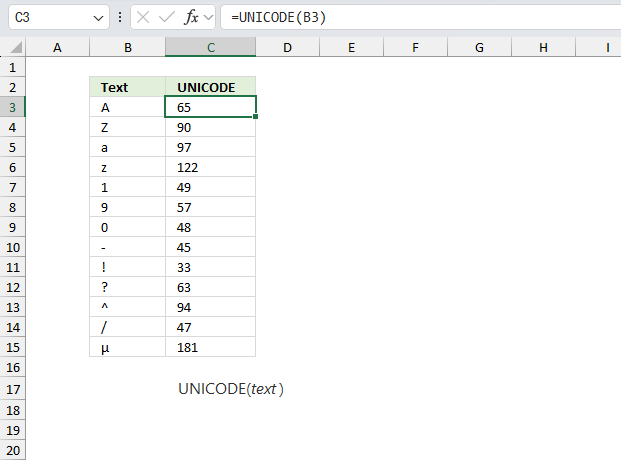
CODE function returns the corresponding number for the first character based on your computers character set. (PC- ANSI)
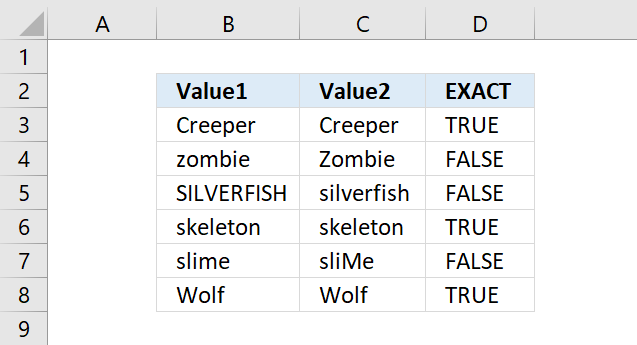
EXACT function checks if two values are precisely the same, it returns TRUE or FALSE. The EXACT function also considers upper case and lower case letters.
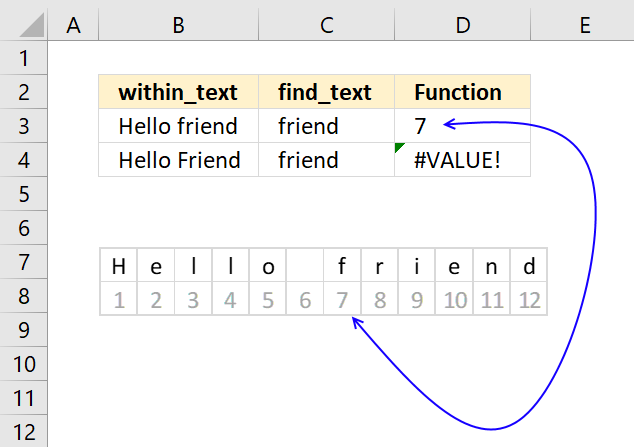
FIND function returns the position of a specific string in another string, reading left to right. Note, the FIND function is case-sensitive.
LEFT function extracts a specific number of characters always starting from the left.
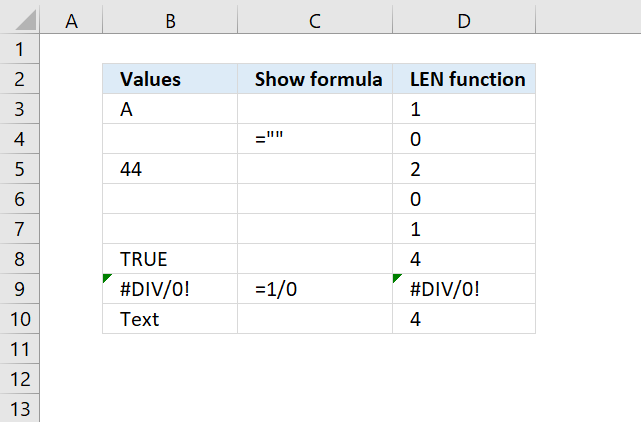
LEN function returns the number of characters in a cell value.
MID function returns a substring from a string based on the starting position and the number of characters you want to extract.
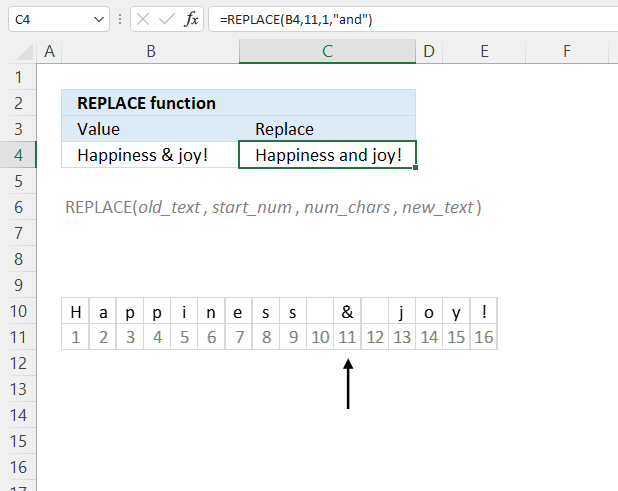
REPLACE function substitutes a part of a text string based on the number of characters and length with a text string you provide.
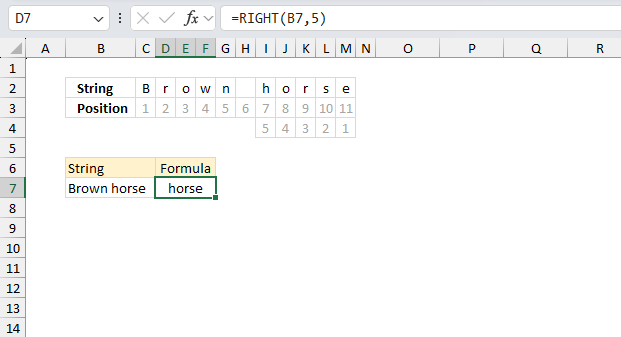
RIGHT function extracts a specific number of characters always starting from the right.
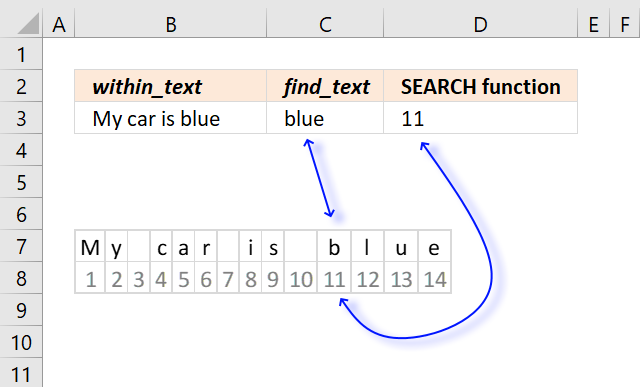
SEARCH function returns the number of the character at which a specific character or text string is found reading left to right (not case-sensitive)
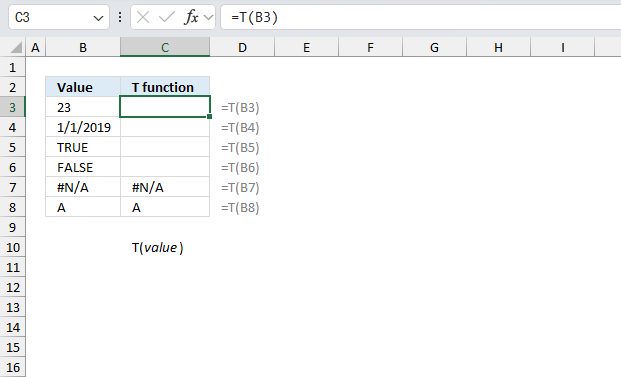
T function returns a text value if the argument is a text value.
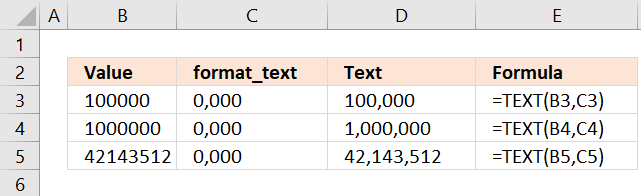
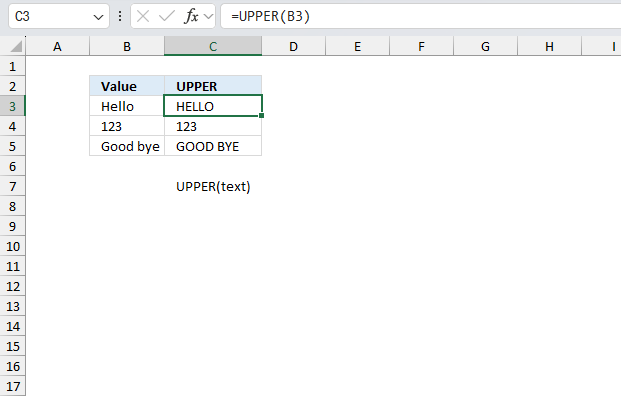
TEXT function converts a value to text in a specific number format.
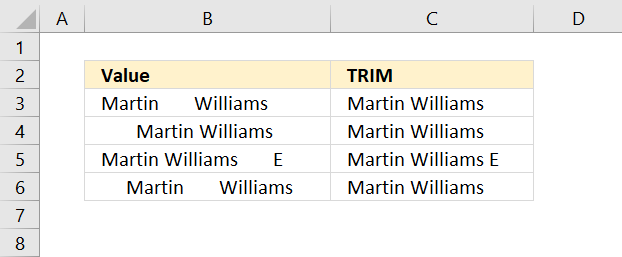
TRIM function deletes all blanks or space characters except single blanks between words in a cell value.
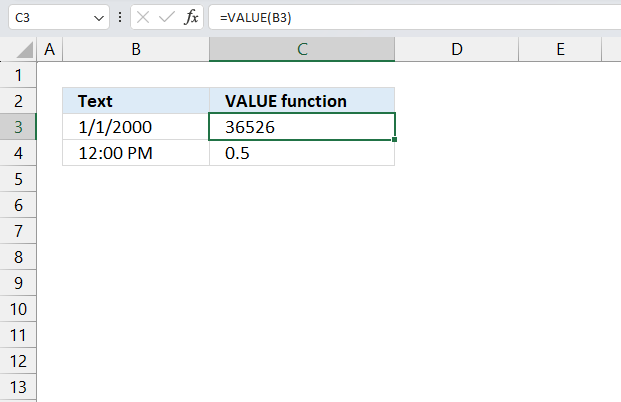
VALUE function converts a text string that represents a number to a number.
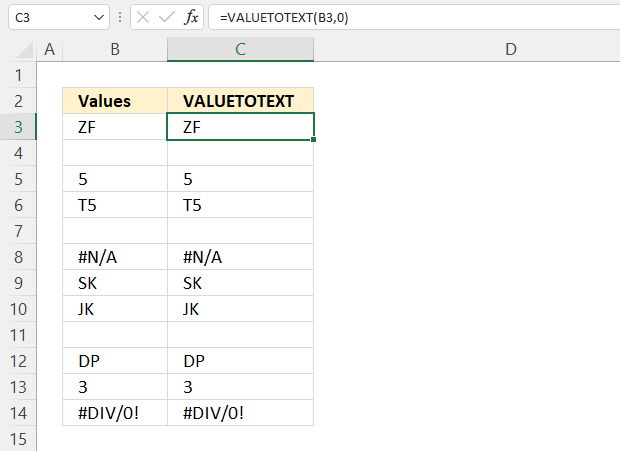
VALUETOTEXT function returns a value in text form. Text values are unmodified and non-text values are converted to text.
Back to top
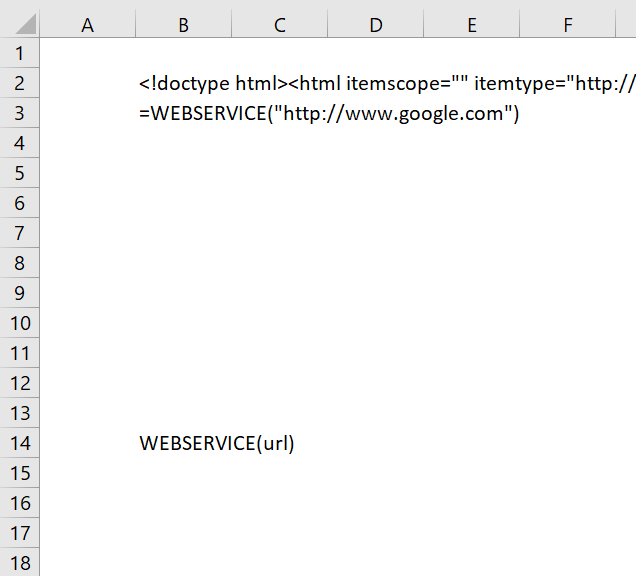
Web
Back to top
Excel Function Basics
The sidebar (or click the hamburger icon if you are on mobile) shows a list of Excel functions based on category. Press CTRL + F in your web browser to quickly search the sidebar for the function you are looking for.
If you rather prefer an alphabetically sorted list then this link takes you to Excel functions sorted from A to Z.
Table of Contents
How to enter a function in Excel
You are now shown the arguments for the chosen function.
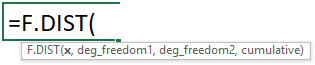
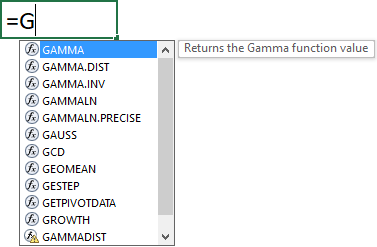
Enter the values for each argument, some arguments display a list of options if the function requires you to enter one of many predetermined parameters, see image below.
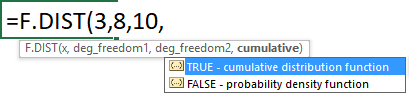
Use the arrow keys to select an argument and press TAB key to choose the selected argument. Type a closing parentheses when all arguments have been entered.
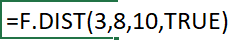
Lastly press ENTER or CTRL + SHIFT + ENTER if the function requires you to.
Back to top
How do I insert a function?
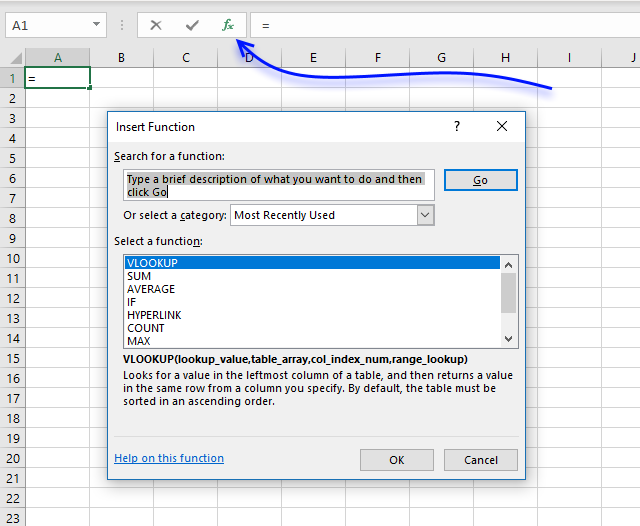
- Select a cell.
- Click the "fx" button next to the formula bar, a dialog box appears.
- The dialog box allows you to search for a function. You can also browse functions based on category or recently used functions.
- The dialog box also specifies the arguments of the selected function which is great if you are not familiar with the selected function.
- At the very bottom of the dialog box is a link that takes you to Microsofts support page based on the function you selected.
- Click the OK button.
This takes you to another dialog box that guides you through each argument in the selected function.
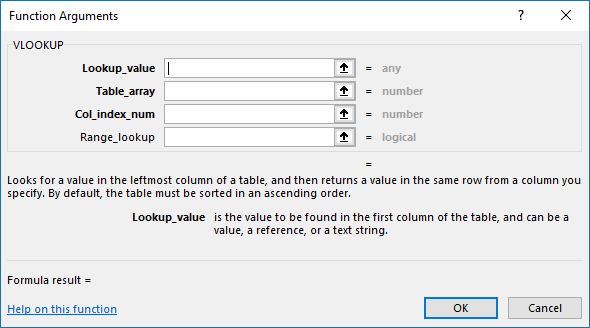
The dialog box describes each argument and lets you select cell(s) in your worksheet in order to complete the function.
Click the OK button when all arguments are specified.
Back to top
How many arguments in a function can I use?
It depends on the function, some lets you use up to 255 arguments and others have none. For example, the SUM function allows you to have up to 255 arguments in one function where as the TODAY function has no arguments.
An argument may contain a cell reference to a single cell or a cell reference to multiple cells, constants, arrays or structured references.
What are the most used functions of Excel?
Excel provides you functions to perform mathematical, statistical and financial calculations.
The most used functions are probably:
Back to top
What are the most useful functions?
It depends who ask, users may have different goals. In general, if you have a task that is tedious and time-consuming there is a great chance there is a feature or function that can help you out.
Start by doing a internet search on what you want to accomplish in Excel, most likely there are others that have had the same problem/question.
Many consider the VLOOKUP function or INDEX - MATCH functions to be immensely powerful. They allow you to do lookups and return another value on the same row as the matching value.
In fact, there are som many functions that most problems you encounter can be solved. Excel lets you also, in most cases, combine several functions in order to build a formula that is exactly what you are looking for.
Back to top
How many functions are there in Excel?
It depends on your Excel version, older versions have fewer functions. There are at least 467 different functions in the latest version.
Back to top
Are the functions categorized?

Yes, there are at least 12 different categories.
Back to top
What are the latest Excel functions?
The following six functions are the latest in the Office 365 subscription:
Back to top
What functions are outdated?
Some functions have been replaced by newer better functions, you can find them in the Compatibility category. They are still working, however, they may be removed in future updates. I recommend that you replace the outdated functions with their newer equivalents.
Back to top
What is an Excel formula?
A formula calculates a value based on the function or functions used. It always begins with a equal sign so Excel can distinguish it from a text or numerical value.
Back to top
What is an array formula?
In general, an array formula calculates multiple values simultaneously and sometimes but not always return multiple values.
To enter an array formula, type the formula in a cell then press and hold CTRL + SHIFT simultaneously, now press Enter once. Release all keys.
The formula bar now shows the formula with a beginning and ending curly bracket telling you that you entered the formula successfully. Don't enter the curly brackets yourself.
This article demonstrates this in greater detail: How to enter an array formula
Back to top
What functions are you required to enter as an array formula?
In general, functions that return more than one value requires you to enter them as an array formula. You must enter the following functions as an array formula in order to make it work properly.
You can also use regular functions in an array formula and when you start doing that you are beginning to discover all the really powerful stuff that is possible with Excel.
Back to top
What is a volatile function?
A volatile function is a function that is recalculated every time the worksheet is calculated. What this means is that it may slow down your workbook considerably.
For example, the TODAY function returns the date each time the worksheet is recalculated to make sure the current day is displayed. This is not cpu intensive if entered in a single cell, however, hundreds or thousands of cells then you may notice a difference.
The following functions are volatile:
Back to top
How do I troubleshoot a function/formula?
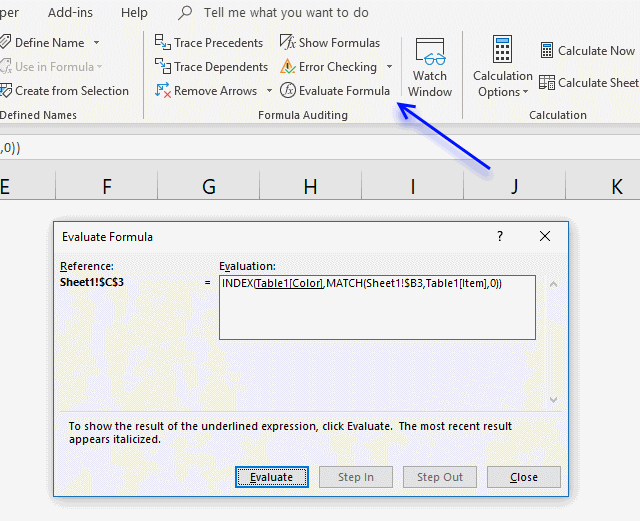
Excel has a built-in feature that allows you to see each step in the formula calculation, this makes it easier to see which function is giving you trouble.
- Select the cell containing the formula you want to troubleshoot.
- Go to tab "Formulas" on the ribbon.
- Click "Evaluate Formula" button, a dialog box appears.
- Click the "Evaluate" button to see each calculation step.
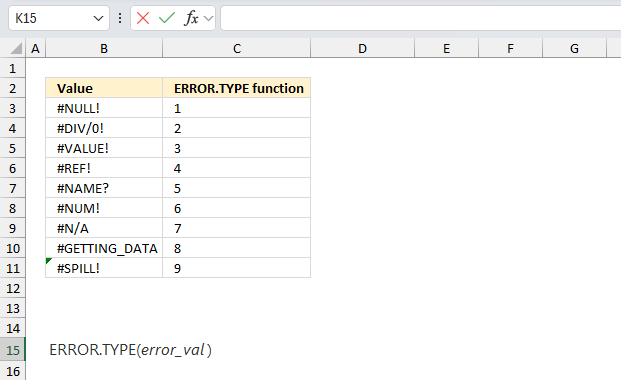
You can also right-click on the cell to see a context menu. This menu allows you to investigate the error further, you can see a descriptive text of the error message.

The second line allows you to see the support page of this error, the third line opens the "Evaluate formula" tool that I demonstrated above.
Back to top
What is a cell reference?
A cell reference is an address to a specific cell in your workbook. Each column is labeled from A to XFD and rows are numbered from 1 to 1048576, a cell reference contains the column letter and the row number like coordinates.
Example, here is a cell reference: Sheet1!G34. Sheet1 is the name of the worksheet the cell is located on. G is the column which is the seventh column from the left, 34 is the row number.
Back to top
What is an array?
Most functions lets you enter arrays in one or more arguments. An array contains multiple values with a comma and/or semicolon as delimiting characters.
The array begins with a curly bracket { and ends with a curly bracket } Here is an example of an array: {"One", 2, "Three"}. Text values must begin an end with double quotes or Excel thinks they are functions.
Back to top