How to use the STANDARDIZE function
What is the STANDARDIZE function?
The STANDARDIZE function calculates a normalized value from a distribution characterized by mean and standard_dev.
Table of Contents
1. Introduction
What is a distribution?
A distribution describes how data is distributed across possible values. It shows the frequency of values.
What is the mean of a distribution?
The average value (arithmetic mean) of a distribution, calculated by summing numbers and dividing by the count.
The AVERAGE function calculates the arithmetic mean.
What is the standard deviation of a distribution?
Standard deviation is a measure of dispersion that indicates how spread out the values in a dataset are from the mean. It is represented by the Greek letter sigma (σ).
The formula for calculating standard deviation is:
σ = √Σ(x - μ)2 / (N - 1)
Where:
σ = Standard deviation
Σ = Sum of
x = Values in the dataset
μ = Mean of the dataset
N = Number of values in the dataset
(N - 1) = Sample correction factor
The STDEV.P and STDEV.S functions calculate the standard deviation.
What is normalizing a distribution?
Normalizing a distribution means rescaling it to have a arithmetic mean of 0 (zero) and standard deviation of 1. See below on how STANDARDIZE function is calculated.
What is a normal distribution?
A symmetrical bell-shaped distribution where data clusters around the mean. Defined by its mean and standard deviation. The NORM.DIST function lets you create a bell-shaped distribution.
What is a standard normal distribution?
A standard normal distribution is a normal distribution with the mean of 0 (zero) and the standard deviation is 1.
Why normalize a distribution?
The shape of the normalized distribution allows you to determine
- the statistical method to use
- identify potential issues with the data (outliers, skewness, kurtosis etc)
- compare distributions across different groups or conditions
2. Syntax
STANDARDIZE(x, mean, standard_dev)
3. Arguments
| x | Required. The value you want to normalize. |
| Mean | Required. The arithmetic mean of the distribution. |
| Standard_dev | Required. The standard deviation of the distribution. |
4. Example 1

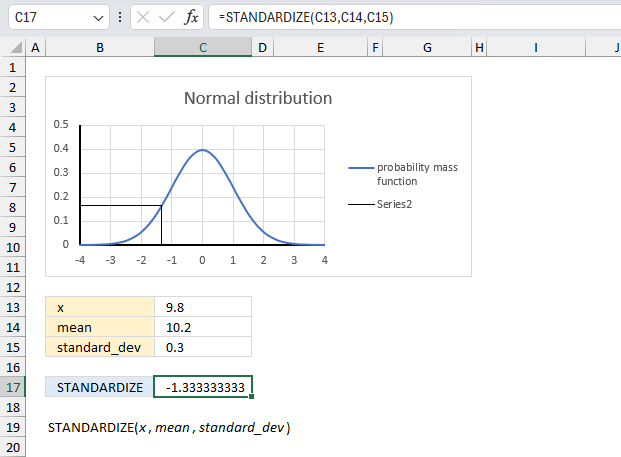
A manufacturing company produces bolts with a target diameter of 10 mm. The process has a mean of 10.2 mm and a standard deviation of 0.3 mm. If a bolt has a diameter of 9.8 mm what is its standardized value?
The arguments are:
- x = 9.8 mm
- mean = 10.2 mm
- standard_dev = 0.3 mm
These arguments are specified in cells C13,C14, and C15 respectively, in the image above.
The image above shows a chart containing a blue curve representing the probability mass function of a normal distribution where the mean is 0 and the standard deviation is 1. The black lines represents the intersection between the standardized value and the blue curve which is the normal distribution.
Formula in cell C17:
The formula returns -1.333333 which represents the standardized x value, you can find that value on the chart above.
In the image above, locate the value 9.8 on the x-axis. From that point, draw an imaginary vertical line upwards until it intersects with the blue curve, which represents the probability mass function for a normal distribution. Then, follow the point of intersection horizontally towards the y-axis to the left. You will find that the corresponding value on the y-axis is approximately 0.164.
You can use the PHI function to calculate the y value:
returns approx. 0.164
5. Example 2
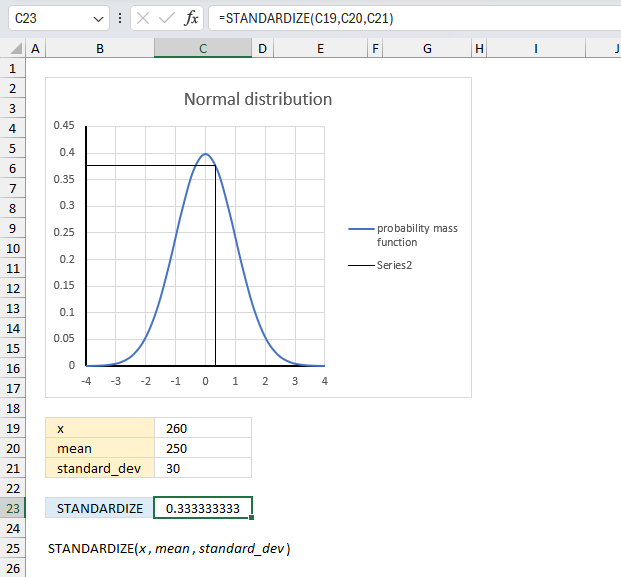
In a study of reaction times the mean response time was 250 milliseconds with a standard deviation of 30 milliseconds. If a participant had a reaction time of 260 milliseconds, what was their standardized reaction time?
The arguments are:
- x = 260 ms
- mean = 250 ms
- standard_dev = 30 ms
These arguments are specified in cells C13,C14, and C15 respectively, in the image above.
The image above shows a chart containing a blue curve representing the probability mass function of a normal distribution where the mean is 0 and the standard deviation is 1. The black lines represents the intersection between the standardized value and the blue curve which is the normal distribution.
Formula in cell C17:
The formula returns 0.333333 which represents the standardized x value, you can find that value on the chart above.
In the image above, locate the value 0.333333 on the x-axis. From that point, draw an imaginary vertical line upwards until it intersects with the blue curve, which represents the probability mass function for a normal distribution. Then, follow the point of intersection horizontally towards the y-axis to the left. You will find that the corresponding value on the y-axis is approximately 0.377.
You can use the PHI function to calculate the y value:
returns approx. 0.377
6. Example 3
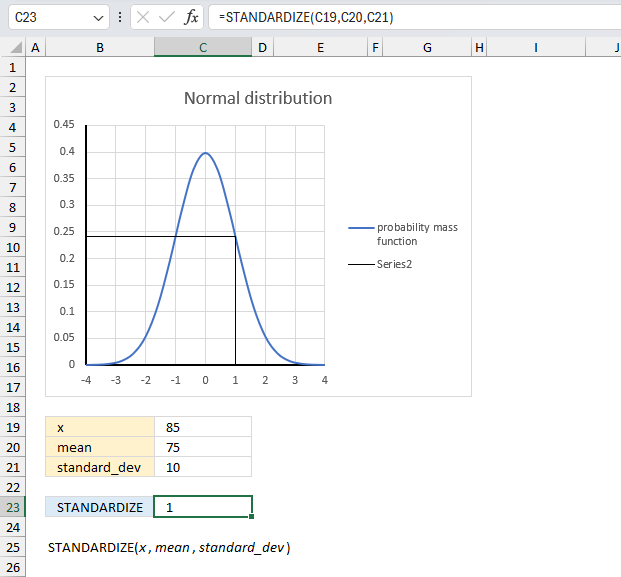
In a class of 50 students the final exam scores were recorded. The mean score was 75 and the standard deviation was 10. If a student scored 85 on the exam what was their standardized score?
The arguments are:
- x = 85
- mean = 75
- standard_dev = 10
These arguments are specified in cells C13,C14, and C15 respectively, in the image above.
The image above shows a chart containing a blue curve representing the probability mass function of a normal distribution where the mean is 0 and the standard deviation is 1. The black lines represents the intersection between the standardized value and the blue curve which is the normal distribution.
Formula in cell C17:
The formula returns 1 which represents the standardized x value, you can find that value on the chart above.
In the image above, locate the value 1 on the x-axis. From that point, draw an imaginary vertical line upwards until it intersects with the blue curve, which represents the probability mass function for a normal distribution. Then, follow the point of intersection horizontally towards the y-axis to the left. You will find that the corresponding value on the y-axis is approximately 0.24.
You can use the PHI function to calculate the y value:
returns approx. 0.24
7. Function not working
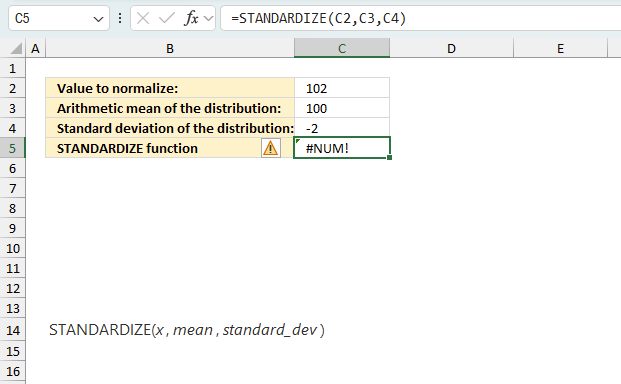
STANDARDIZE function returns a #NUM! error if argument standard_dev is equal to or less than 0 (zero).
7.1 Troubleshooting the error value
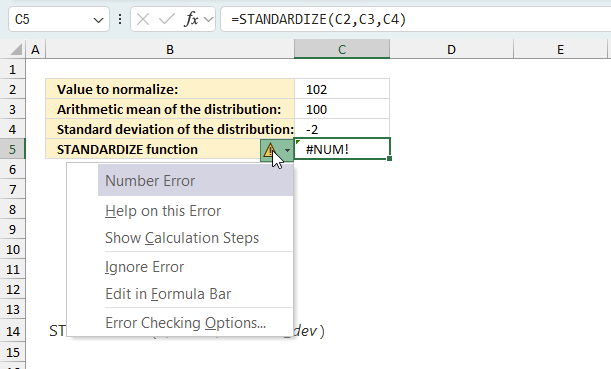
When you encounter an error value in a cell a warning symbol appears, displayed in the image above. Press with mouse on it to see a pop-up menu that lets you get more information about the error.
- The first line describes the error if you press with left mouse button on it.
- The second line opens a pane that explains the error in greater detail.
- The third line takes you to the "Evaluate Formula" tool, a dialog box appears allowing you to examine the formula in greater detail.
- This line lets you ignore the error value meaning the warning icon disappears, however, the error is still in the cell.
- The fifth line lets you edit the formula in the Formula bar.
- The sixth line opens the Excel settings so you can adjust the Error Checking Options.
Here are a few of the most common Excel errors you may encounter.
#NULL error - This error occurs most often if you by mistake use a space character in a formula where it shouldn't be. Excel interprets a space character as an intersection operator. If the ranges don't intersect an #NULL error is returned. The #NULL! error occurs when a formula attempts to calculate the intersection of two ranges that do not actually intersect. This can happen when the wrong range operator is used in the formula, or when the intersection operator (represented by a space character) is used between two ranges that do not overlap. To fix this error double check that the ranges referenced in the formula that use the intersection operator actually have cells in common.
#SPILL error - The #SPILL! error occurs only in version Excel 365 and is caused by a dynamic array being to large, meaning there are cells below and/or to the right that are not empty. This prevents the dynamic array formula expanding into new empty cells.
#DIV/0 error - This error happens if you try to divide a number by 0 (zero) or a value that equates to zero which is not possible mathematically.
#VALUE error - The #VALUE error occurs when a formula has a value that is of the wrong data type. Such as text where a number is expected or when dates are evaluated as text.
#REF error - The #REF error happens when a cell reference is invalid. This can happen if a cell is deleted that is referenced by a formula.
#NAME error - The #NAME error happens if you misspelled a function or a named range.
#NUM error - The #NUM error shows up when you try to use invalid numeric values in formulas, like square root of a negative number.
#N/A error - The #N/A error happens when a value is not available for a formula or found in a given cell range, for example in the VLOOKUP or MATCH functions.
#GETTING_DATA error - The #GETTING_DATA error shows while external sources are loading, this can indicate a delay in fetching the data or that the external source is unavailable right now.
7.2 The formula returns an unexpected value
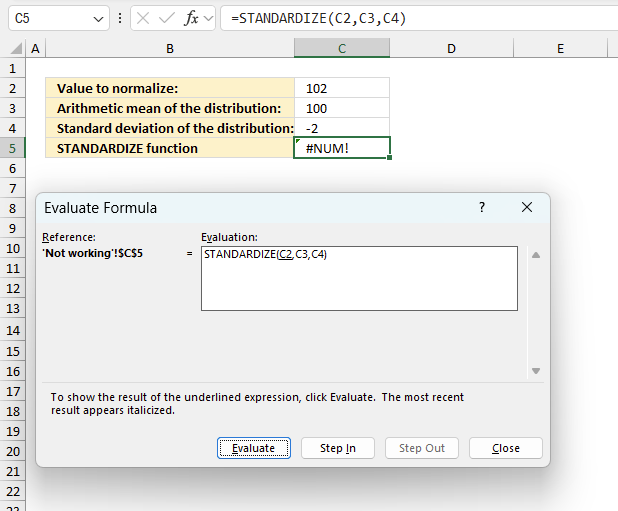
To understand why a formula returns an unexpected value we need to examine the calculations steps in detail. Luckily, Excel has a tool that is really handy in these situations. Here is how to troubleshoot a formula:
- Select the cell containing the formula you want to examine in detail.
- Go to tab “Formulas” on the ribbon.
- Press with left mouse button on "Evaluate Formula" button. A dialog box appears.
The formula appears in a white field inside the dialog box. Underlined expressions are calculations being processed in the next step. The italicized expression is the most recent result. The buttons at the bottom of the dialog box allows you to evaluate the formula in smaller calculations which you control. - Press with left mouse button on the "Evaluate" button located at the bottom of the dialog box to process the underlined expression.
- Repeat pressing the "Evaluate" button until you have seen all calculations step by step. This allows you to examine the formula in greater detail and hopefully find the culprit.
- Press "Close" button to dismiss the dialog box.

There is also another way to debug formulas using the function key F9. F9 is especially useful if you have a feeling that a specific part of the formula is the issue, this makes it faster than the "Evaluate Formula" tool since you don't need to go through all calculations to find the issue..
- Enter Edit mode: Double-press with left mouse button on the cell or press F2 to enter Edit mode for the formula.
- Select part of the formula: Highlight the specific part of the formula you want to evaluate. You can select and evaluate any part of the formula that could work as a standalone formula.
- Press F9: This will calculate and display the result of just that selected portion.
- Evaluate step-by-step: You can select and evaluate different parts of the formula to see intermediate results.
- Check for errors: This allows you to pinpoint which part of a complex formula may be causing an error.
The image above shows cell reference C4 converted to hard-coded value using the F9 key. The STANDARDIZE function requires numerical values larger than or equal to 0 (zero) which is not the case in this example. We have found what is wrong with the formula.
Tips!
- View actual values: Selecting a cell reference and pressing F9 will show the actual values in those cells.
- Exit safely: Press Esc to exit Edit mode without changing the formula. Don't press Enter, as that would replace the formula part with the calculated value.
- Full recalculation: Pressing F9 outside of Edit mode will recalculate all formulas in the workbook.
Remember to be careful not to accidentally overwrite parts of your formula when using F9. Always exit with Esc rather than Enter to preserve the original formula. However, if you make a mistake overwriting the formula it is not the end of the world. You can “undo” the action by pressing keyboard shortcut keys CTRL + z or pressing the “Undo” button
7.3 Other errors
Floating-point arithmetic may give inaccurate results in Excel - Article
Floating-point errors are usually very small, often beyond the 15th decimal place, and in most cases don't affect calculations significantly.
8. How is the STANDARDIZE function calculated?
You can standardize any normal distribution like this:
z = (x - µ)/σ
z = z-score
µ is the mean.
σ is the standard deviation.
Functions in 'Statistical' category
The STANDARDIZE function function is one of 73 functions in the 'Statistical' category.
How to comment
How to add a formula to your comment
<code>Insert your formula here.</code>
Convert less than and larger than signs
Use html character entities instead of less than and larger than signs.
< becomes < and > becomes >
How to add VBA code to your comment
[vb 1="vbnet" language=","]
Put your VBA code here.
[/vb]
How to add a picture to your comment:
Upload picture to postimage.org or imgur
Paste image link to your comment.
Contact Oscar
You can contact me through this contact form