How to use the PRICEMAT function
What is the PRICEMAT function?
The PRICEMAT function calculates the price per $100 nominal value of a bond that pays interest at maturity.
Table of Contents
1. Introduction
What is the nominal value for a bond?
The nominal value, also called the par value or face value, is the amount a bond is issued and redeemed for by the bond issuer. It's the stated value of the bond.
What is interest?
Interest refers to the periodic coupon payments made by a bond issuer to bondholders over the bond's lifetime. However, the PRICEMAT function works for bonds that pay interest at maturity.
What is bond maturity?
Bond maturity is the date when a bond's term ends, at which point the issuer must repay the bond's par value and any final interest due to bondholders. A 30-year bond issued today will have a maturity date 30 years from now.
2. Syntax
PRICEMAT(settlement, maturity, issue, rate, yld, [basis])
| settlement | Required. The bond's settlement date. |
| maturity | Required. The bond's maturity date, in other words, when it expires. |
| issue | Required. The bond's issue date. |
| rate | Required. The bond's interest rate at date of issue. |
| yld | Required. The bond's annual return. |
| [basis] | Optional. Day count basis.
0 (zero) - US (NASD) 30/360 (default value) 1 - Actual/actual 2 - Actual/360 3 - Actual/365 4 - European 30/360 |
What is the bond's settlement date?
A bond's settlement date is the date when the trade is finalized and the bond is delivered to the buyer in exchange for payment to the seller. Settlement for US treasury bonds is usually T+1 day.
What is the bonds issue date?
A bond's issue date is the original date when the bond was first offered and sold to investors on the primary market by the issuing entity. The bond's coupon payment schedules are aligned with the issue date.
What is the bond's interest rate at date of issue?
The interest rate at a bond's issue date, also called the coupon rate, is the annual interest rate the bond will pay throughout its lifetime based on the bond's par value. A 5% coupon rate means the bond will pay 5% of par annually.
What is the bond's annual return?
A bond's annual return is the gain or loss in value over a one year holding period plus any interest income. It factors in both bond price appreciation/depreciation and the interest coupons received.
3. Example 1

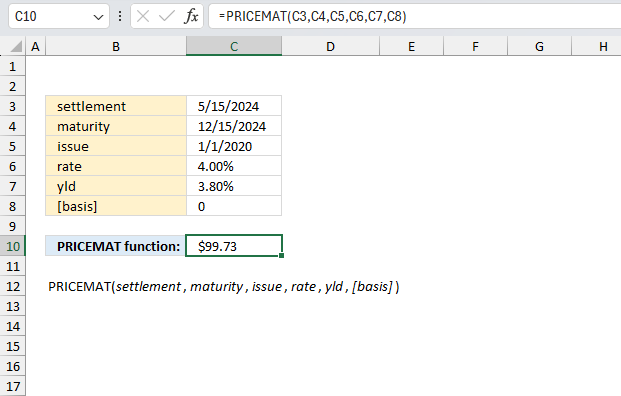
You are considering investing in a 5-year bond issued on 1/1/2020 that pays 4% annual coupons. The settlement date is 5/15/2024, maturity is 12/15/2024, the yield is 3.8%, and day count basis is 30/360. What is the price per $100 face value?
The PRICEMAT function takes the following arguments:
- settlement (C3) - 5/15/2024
- maturity (C4) - 12/15/2024
- issue (C5) - 1/1/2020
- rate (C6) - 4.00%
- yld (C7) - 3.80%
- [basis] (C8) - 0
The PRICEMAT function calculates the price per $100 nominal value of a bond that pays interest at maturity based on these inputs.
Formula in cell C10:
The returned value shown in cell C10 is $99.73.
The math formula behind the PRICEMAT function is: (100 + ((DIM / B) * rate * 100)) / (1 + (DSM / B) * yld) - ((A / B) * rate * 100)
Lets plug in the values and see what we get. Calculating the number of days:
- B = 360 (number of days in a year for 30/360 convention)
- DSM = 214 days (from settlement 5/15/2024 to maturity 12/15/2024)
- DIM = 1,810 days (from issue 1/1/2020 to maturity 12/15/2024)
- A = 1,596 days (from issue 1/1/2020 to settlement 5/15/2024)
- rate = 0.04
- yld = 0.038
PRICEMAT = (100 + ((DIM / B) * rate * 100)) / (1 + (DSM / B) * yld) - ((A / B) * rate * 100)
(100+((1810/360)*0.04*100))/(1+(214/360)*0.038)-((1596/360)*0.04*100)
Step 1: Calculate (1810/360)
1810/360 = 5.0277777777777775
Step 2: Calculate (5.0277777777777775 * 0.04 * 100)
5.0277777777777775 * 0.04 * 100 = 20.111111111111112
Step 3: Calculate (100 + 20.111111111111112)
100 + 20.111111111111112 = 120.11111111111111
Step 4: Calculate (214/360)
214/360 = 0.5944444444444444
Step 5: Calculate (0.5944444444444444 * 0.038)
0.5944444444444444 * 0.038 = 0.022588888888888887
Step 6: Calculate (1 + 0.022588888888888887)
1 + 0.022588888888888887 = 1.022588888888889
Step 7: Calculate (120.11111111111111 / 1.022588888888889)
120.11111111111111 / 1.022588888888889 = 117.4440406475142
Step 8: Calculate (1596/360)
1596/360 = 4.433333333333333
Step 9: Calculate (4.433333333333333 * 0.04 * 100)
4.433333333333333 * 0.04 * 100 = 17.733333333333334
Step 10: Calculate (117.4440406475142 - 17.733333333333334)
117.4440406475142 - 17.733333333333334 = 99.7245350399675
(100+((1810/360)*0.04*100))/(1+(214/360)*0.038)-((1596/360)*0.04*100) = 99.7245350399675
4. Example 2
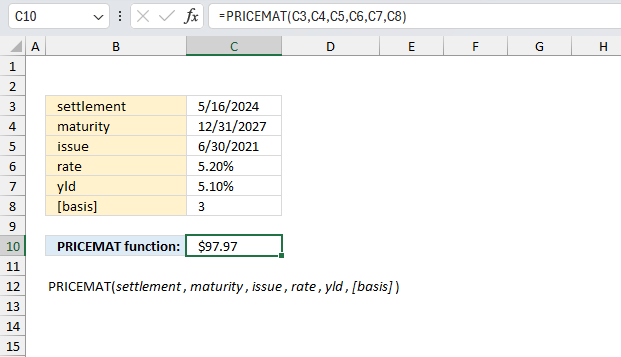
A 7-year bond matures on 12/31/2027 with a face value of $1,000. It was issued on 6/30/2021 at 99.5 with a 5.2% annual coupon rate. If the settlement date is 5/16/2024 and the yield is 5.1% based on actual/365 day count, calculate the price?
The arguments and their provided values are:
- settlement (C3): 5/16/2024
- maturity (C4): 12/31/2027
- issue (C5): 6/30/2021
- rate (C6): 5.20% (or 0.052 in decimal form)
- yld (C7): 5.10% (or 0.051 in decimal form)
- [basis] (C8): 3 (likely indicating the actual/365 day count convention)
The PRICEMAT function calculates the price per $100 nominal value of a bond that pays interest at maturity based on these inputs.
Formula in cell C10:
The returned value shown in cell C10 is $97.97 which represents the $100 face value. We need to multiply by 10 to get the $1000 face value. 97.97 * 10 = $979.70
The PRICEMAT value is calculated using this math formula:
PRICEMAT = (100 + ((DIM / B) * rate * 100)) / (1 + (DSM / B) * yld) - ((A / B) * rate * 100)
- B = 365 (number of days in a year for actual/365 basis)
- DSM = 959 days (from settlement 5/16/2024 to maturity 12/31/2027)
- DIM = 2,376 days (from issue 6/30/2021 to maturity 12/31/2027)
- A = 1,417 days (from issue 6/30/2021 to settlement 5/16/2024)
- rate = 0.052 (5.20% annual coupon rate)
- yld = 0.051 (5.10% annual yield)
Plugging in the values:
PRICEMAT = (100 + ((2376 / 365) * 0.052 * 100)) / (1 + (959 / 365) * 0.051) - ((1417 / 365) * 0.052 * 100)
= (100 + 339.1781) / (1 + 2.6271 * 0.051) - (202.4274)
= 439.1781 / 1.1339 - 202.4274
= 387.2727 - 202.4274
= $97.97
So based on the given inputs and the PRICEMAT formula, the calculated price is $97.97, which matches the value shown in cell C10.
5. Why is the function not working?
Settlement, maturity, issue, and basis are shortened to integers.
The PRICEMAT function returns:
#NUM! error value if
rate < 0
yld < 0
basis < 0
basis > 4
settlement >= maturity
#VALUE! error value if
settlement, issue or maturity is not a valid date. Use the DATE function in the PRICEMAT function to avoid errors. Example DATE(2010, 11, 5) is 5th November, 2010.
6. How is this function calculated?
The following formula demonstrates how the PRICEMAT function calculates it's value, in other words, the math formula behind the function.
| B | Days in year. |
| DSM | Days from settlement to maturity. |
| DIM | Number of days from issue to maturity. |
| A | Number of days from issue to settlement. |
The text representation of the formula is:
PRICEMAT = (100 + ((DIM / B) * rate * 100)) / (1 + (DSM / B) * yld) - ((A / B) * rate * 100)
Where:
- B is the number of days in a year.
- DSM is the number of days from settlement to maturity.
- DIM is the number of days from issue to maturity.
- A is the number of days from issue to settlement.
- rate is the annual interest rate or coupon rate.
- yld is the annual yield or required return on the bond.
Functions in 'Financial' category
The PRICEMAT function function is one of 27 functions in the 'Financial' category.
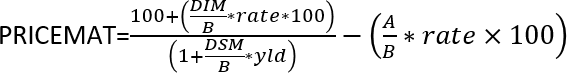
How to comment
How to add a formula to your comment
<code>Insert your formula here.</code>
Convert less than and larger than signs
Use html character entities instead of less than and larger than signs.
< becomes < and > becomes >
How to add VBA code to your comment
[vb 1="vbnet" language=","]
Put your VBA code here.
[/vb]
How to add a picture to your comment:
Upload picture to postimage.org or imgur
Paste image link to your comment.
Contact Oscar
You can contact me through this contact form