How to use the DDB function
What is the DDB function?
The DDB function calculates the depreciation of an asset for a given period using the double-declining balance method or based on user input.
Table of Contents
1. Introduction
What is depreciation of an asset?
Depreciation is an accounting method that allows businesses to allocate the cost of a tangible asset over its useful life. It represents how much of an asset’s value has been used up over time.
Depreciation helps businesses to match their expenses with their revenues, and to reduce their taxable income by deducting the depreciation expense.
What is the double-declining balance method?
The double-declining balance method is an accelerated depreciation technique used in accounting and finance, it is a specific application of the declining balance method.
Depreciation is calculated by multiplying the asset's book value by a fixed rate of 200% each year. This results in the asset being fully depreciated over roughly half the straight-line depreciation schedule.
The depreciation amount declines each year as the asset's book value declines, depreciation is highest in the first year, tapering down each subsequent year.
2. Syntax
DDB(cost, salvage, life, period, [factor])
| Cost | Required. What you pay for the asset. |
| Salvage | Required. The value of the asset at the end of depreciation. |
| Life | Required. The number of periods the asset is being depreciated. |
| Period | Required. The period you want to know the depreciation of. |
| [factor] | Optional. How quickly the balance declines, default value is 2 (the double-declining balance method). |
3. Example 1

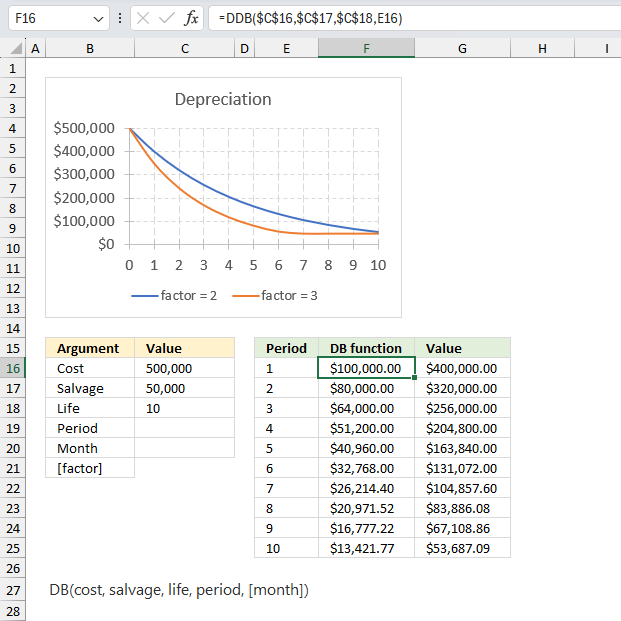
A company purchased a machine for $500,000 with an estimated salvage value of $50,000 after 10 years of useful life. Calculate the depreciation expense for each year using the double declining balance method?
This example demonstrates the depreciation of an asset valued 500,000 across 10 periods ending with a salvage value of 50,000 using the double-declining balance method. The example shows that depreciation is larger for the initial periods.
Here are the arguments:
- Cost: This argument represents the initial cost of the asset. In the example, the cost is set to $500,000.
- Salvage: This argument is the estimated salvage value of the asset at the end of its useful life. In the example, it is set to $50,000.
- Life: This argument is the total number of periods over which the asset will be depreciated. In the example, it is set to 10.
- Period: This argument specifies the period for which the depreciation is calculated.
- Month (optional): This argument is not used in the example, but it is a logical value indicating whether the periods are months or not.
- [factor]: This argument is optional and represents the rate at which the balance declines. In the example, it is not explicitly set, but the chart shows depreciation patterns for factor values of 2 and 3.
Formula in cell F16:
The DDB function calculates the decline in value for each period from 1 to 10, the remaining value of the asset is shown in cell range G16:G25. The cost value is specified in cell C16 and the salvage value is specified in cell C17. Lastly, the number of periods is specified in cell C18. The DDB function calculates the depreciation for a given period using these input values.
The chart above titled "Depreciation" illustrates the depreciation pattern over the 10 periods using the DDB function. The blue line represents the depreciation pattern when the factor is set to 2 (double declining balance), while the orange line represents the depreciation pattern when the factor is set to 3 (triple declining balance).
The chart shows that with a higher factor value, the depreciation is more accelerated in the early periods and decreases at a faster rate in the later periods. This behavior is typical of the double declining balance method, where a higher factor value results in a more aggressive depreciation schedule.
The "DB function" and "Value" columns in the data table provide the calculated depreciation values for each period using the DDB function with the given arguments.
4. Example 2
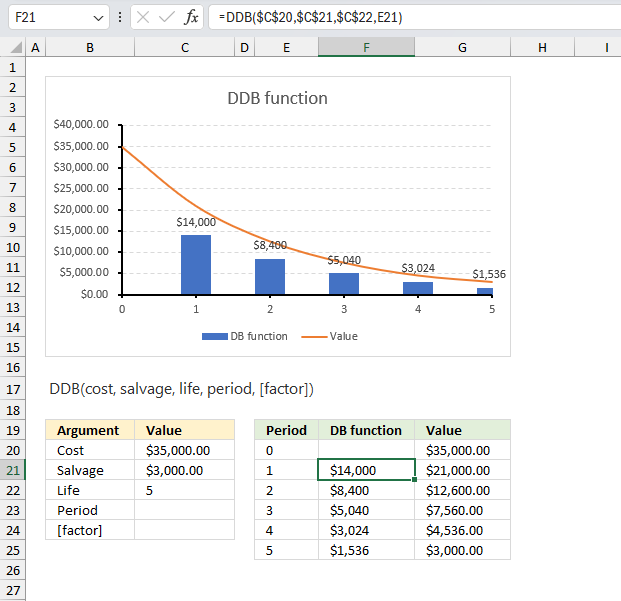
An organization acquired a vehicle for $35,000, with an estimated salvage value of $3,000 after 5 years of use. Determine the yearly depreciation expense using the double declining balance method?
Here are the arguments:
- Cost: This argument represents the initial cost of the asset. In the example, the cost is set to $500,000.
- Salvage: This argument is the estimated salvage value of the asset at the end of its useful life. In the example, it is set to $50,000.
- Life: This argument is the total number of periods over which the asset will be depreciated. In the example, it is set to 10.
- Period: This argument specifies the period for which the depreciation is calculated.
- Month (optional): This argument is not used in the example, but it is a logical value indicating whether the periods are months or not.
- [factor]: This argument is optional and represents the rate at which the balance declines. In the example, it is not explicitly set, but the chart shows depreciation patterns for factor values of 2 and 3.
Formula in cell F21:
The DDB function calculates the decline in value for each period from 1 to 10, the remaining value of the asset is shown in cell range G20:G25. The cost value is specified in cell C20 and the salvage value is specified in cell C21. Lastly, the number of periods is specified in cell C22. The DDB function calculates the depreciation for a given period using these input values.
The chart in the image above shows the decreasing value of the vehicle over the years represented by the orange curve. The blue columns shows the depreciation for years 1 to 5, the data labels above the columns shows the exact values.
The following table shows the depreciation and the value of the vehicle from year 1 to 5:
| Period | Depreciation | Value |
| 0 | $35,000.00 | |
| 1 | $14,000 | $21,000.00 |
| 2 | $8,400 | $12,600.00 |
| 3 | $5,040 | $7,560.00 |
| 4 | $3,024 | $4,536.00 |
| 5 | $1,536 | $3,000.00 |
Period 0 (zero) shows the cost which we specified in cell C20, period 5 shows the salvage value we specified in cell C21.
How is the DDB function calculated?
Here is how the DDB function calculates the depreciation of a period:
Min( (cost - total depreciation from prior periods) * (factor/life), (cost - salvage - total depreciation from prior periods) )
Functions in 'Financial' category
The DDB function function is one of 27 functions in the 'Financial' category.
How to comment
How to add a formula to your comment
<code>Insert your formula here.</code>
Convert less than and larger than signs
Use html character entities instead of less than and larger than signs.
< becomes < and > becomes >
How to add VBA code to your comment
[vb 1="vbnet" language=","]
Put your VBA code here.
[/vb]
How to add a picture to your comment:
Upload picture to postimage.org or imgur
Paste image link to your comment.
Contact Oscar
You can contact me through this contact form