How to use the DB function
What is the DB function?
The DB function calculates the depreciation of an asset for a given period using the fixed-declining balance method.
Table of Contents
1. Introduction
What is depreciation of an asset?
Depreciation is an accounting method that allows businesses to allocate the cost of a tangible asset over its useful life. It represents how much of an asset’s value has been used up over time.
Depreciation helps businesses to match their expenses with their revenues, and to reduce their taxable income by deducting the depreciation expense.
What is fixed-declining balance method?
The fixed-declining balance method is an accelerated depreciation method used to depreciate assets faster than straight-line depreciation.
A fixed rate or percentage is applied each year to the remaining book value, this causes the depreciation amount to decline each year as the book value declines.
Results in higher depreciation early on and lower depreciation later compared to straight-line. Useful for assets expected to lose more value early on in their lifespan.
How is the DB function calculated?
The DB function calculates the depreciation of a period like this:
(cost - total depreciation from prior periods) * rate
where:
rate = 1 - ((salvage / cost) ^ (1 / life))
The first period is calculated like this:
cost * rate * [month] / 12
The last period is calculated like this:
((cost - total depreciation from prior periods) * rate * (12 - [month])) / 12
2. Syntax
DB(cost, salvage, life, period, [month])
| Cost | Required. What you pay for the asset. |
| Salvage | Required. The value of the asset at the end of depreciation. |
| Life | Required. The number of periods the asset is being depreciated. |
| Period | Required. The period you want to know the depreciation of. |
| [Month] | Optional. The number of months in the first year. |
3. Example 1

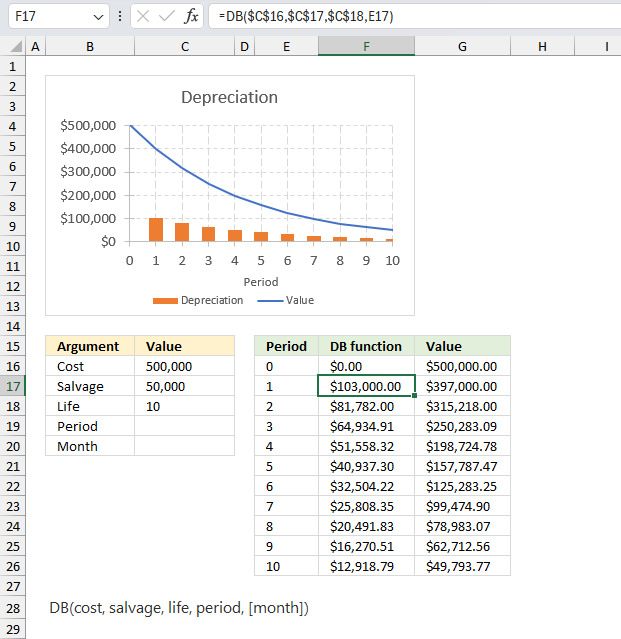
A company purchased a new machine for $500,000 with an estimated salvage value of $50,000 after 10 years of useful life. Calculate the depreciation expense for each year using the declining balance method?
This example demonstrates the depreciation of an asset valued 500,000 across 10 periods ending with a salvage value of 50,000. The example shows that depreciation is larger the initial periods which is shown in the chart above.
Arguments for the DB function:
- Cost: The initial cost of the asset ($500,000 in the example)
- Salvage: The estimated salvage value of the asset at the end of its useful life ($50,000 in the example)
- Life: The total number of periods over which the asset will be depreciated (10 years in the example)
- Period: The specific period for which the depreciation is calculated (ranging from 0 to 10 in the example)
- Month (optional): A logical value indicating whether the periods are months (not used in this example)
Formula in cell F17:
The DB function calculates the decline in value for each period from 1 to 10, the remaining value of the asset is shown in cell range G16:G26. The cost value is specified in cell C16 and the salvage value is specified in cell C17. Lastly, the number of periods is specified in cell C18. The DB function calculates the depreciation for a given period using these input values.
The chart above shows the depreciation pattern with the orange bars representing the depreciation amount for each period and the blue curve representing the remaining value of the asset over time. The pattern follows the declining balance method, where the depreciation is higher in the initial periods and gradually decreases over time.
Lets calculate this example manually using the appropriate math formula:
(cost - total depreciation from prior periods) * rate
where:
rate = 1 - ((salvage / cost) ^ (1 / life))
rate = 1 - (50000/500000)^(1/10) = 0.205671765275719
Period 1: Depreciation = (500000 - 0)*0.205671765275719 = 102835.88
Period 2: Depreciation = (500000 - 102835.88)*0.205671765275719 = 81685.45
Period 3: Depreciation = (500000 - 184521.33)*0.205671765275719 = 64885.06
4. Example 2
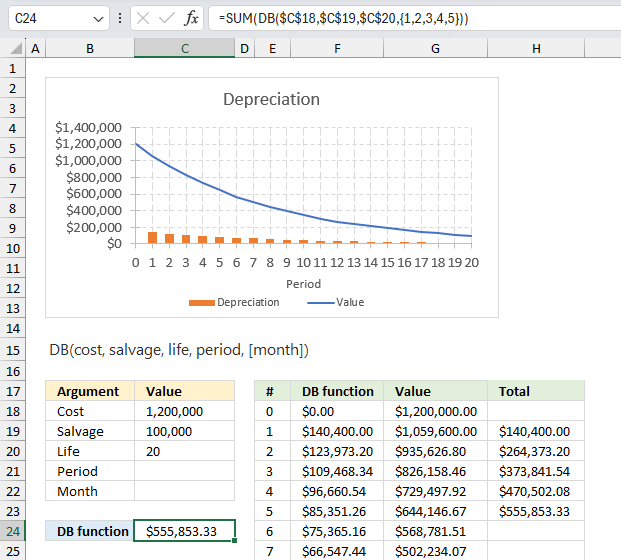
A manufacturing company bought a new production line for $1,200,000, with an estimated salvage value of $100,000 after 20 years of useful life. Determine the total depreciation expense after 5 years using the declining balance method?
Arguments for the DB function:
- Cost: The initial cost of the asset ($1,200,000 in the example)
- Salvage: The estimated salvage value of the asset at the end of its useful life ($100,000 in the example)
- Life: The total number of periods over which the asset will be depreciated (20 years in the example)
- Period: The specific period for which the depreciation is calculated (ranging from 1 to 5 in the example)
- Month (optional): A logical value indicating whether the periods are months (not used in this example)
Formula in cell C24:
The DB function calculates the decline in value for each period from 1 to 5, the remaining value of the asset is shown in cell range G19:G25. The cost value is specified in cell C18 and the salvage value is specified in cell C19. Lastly, the number of periods is specified in cell C20. The DB function calculates the depreciation for a given period using these input values.
Cell C24 returns the total depreciation which is 555,853.33 This is the same number as in cell H23. H23 is the running total based on depreciation for periods 1 to 5.
Explaining formula
Step 1 - Determine the periods
We want to calculate the depreciation for periods 1, 2, 3,4, and 5, to accomplish that we can use curly brackets to specify five different constants: {1,2,3,4,5}
This requires us to enter the formula as an array formula. Excel 365 subscribers may enter the formula as a regular formula.
Step 2 - Calculate the depreciation for each period
DB($C$18,$C$19,$C$20,{1,2,3,4,5})
becomes
DB(1200000,100000,20,{1,2,3,4,5})
and returns {140400,123973.2,109468.3356,96660.5403348,85351.2571156284}
Step 3 - Calculate the total
The SUM function allows you to add numerical values, the function returns the sum in the cell it is entered in. The SUM function is cleverly designed to ignore text and boolean values, adding only numbers.
Function syntax: SUM(number1, [number2], ...)
SUM(DB($C$18,$C$19,$C$20,{1,2,3,4,5}))
becomes
SUM({140400,123973.2,109468.3356,96660.5403348,85351.2571156284})
and returns 555853.33
5. Example 3
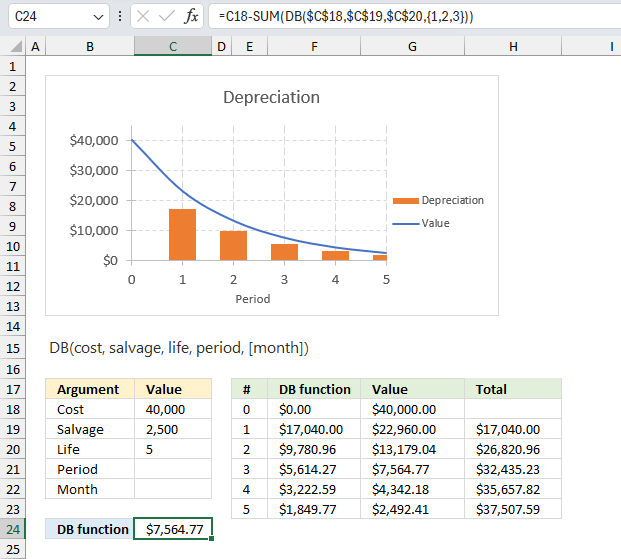
A business acquired a delivery van for $40,000, with an estimated salvage value of $2,500 after 5 years of use. Determine the value of the delivery van after 3 years using the declining balance method?
Arguments for the DB function:
- Cost: The initial cost of the asset ($40,000 in the example)
- Salvage: The estimated salvage value of the asset at the end of its useful life ($2,500 in the example)
- Life: The total number of periods over which the asset will be depreciated (5 years in the example)
- Period: The specific period for which the depreciation is calculated (ranging from 1 to 3 in the example)
- Month (optional): A logical value indicating whether the periods are months (not used in this example)
Formula in cell C24:
The formula returns 7564.77 which is the value after 3 years based on the declining balance method.
Explaining formula
Step 1 - Determine the periods
We want to calculate the depreciation for periods 1, 2, and 3, to accomplish that we can use curly brackets to specify five different constants: {1,2,3}
This requires us to enter the formula as an array formula. Excel 365 subscribers may enter the formula as a regular formula.
Step 2 - Calculate the depreciation for each period
DB($C$18,$C$19,$C$20,{1,2,3})
becomes
DB(40000,2500,5,{1,2,3})
and returns {17040,9780.96,5614.27104}
Step 3 - Calculate the total
The SUM function allows you to add numerical values, the function returns the sum in the cell it is entered in. The SUM function is cleverly designed to ignore text and boolean values, adding only numbers.
Function syntax: SUM(number1, [number2], ...)
SUM(DB($C$18,$C$19,$C$20,{1,2,3,4,5}))
becomes
SUM({17040,9780.96,5614.27104})
and returns 32435.23104
Step 4 - Calculate the value
The minus character lets you calculate the difference between two numerical values. In this particular example, the original cost minus the total of 3 periods of depreciation equals what is left of the value of the delivery van.
C18-SUM(DB($C$18,$C$19,$C$20,{1,2,3}))
40000-32435.23104 equals 7564.76896
Functions in 'Financial' category
The DB function function is one of 27 functions in the 'Financial' category.
How to comment
How to add a formula to your comment
<code>Insert your formula here.</code>
Convert less than and larger than signs
Use html character entities instead of less than and larger than signs.
< becomes < and > becomes >
How to add VBA code to your comment
[vb 1="vbnet" language=","]
Put your VBA code here.
[/vb]
How to add a picture to your comment:
Upload picture to postimage.org or imgur
Paste image link to your comment.
Contact Oscar
You can contact me through this contact form