Finding the shortest path – A * pathfinding
What's on this page
1. Introduction
What means the shortest path?
The shortest path is the minimum distance or cost required to go from one point to another in a graph or network.
It could mean, the least number of steps, the smallest total weight (cost), the fastest route, depending on the problem. Example: On a city map, the shortest path between two streets might be the fastest walking route.
Why find the shortest path?
Finding the shortest path is useful because it helps save time by finding the fastest travel route. It save resources finding cheapest delivery route. Solves optimization problems like network routing, AI path-finding, etc. Here are some real-life user-cases:
- GPS navigation
- Internet routing
- Robotics movement
- Game AI
- Logistics and delivery planning
What is the Manhattan distance method?
Manhattan Distance is a way to measure distance between two points if you can only move horizontally or vertically like on a grid of city streets or in a computer game.
Manhattan Distance = |x1 - x2| + |y1 - y2|
What is Dijkstra's algorithm?
Dijkstra's algorithm finds the shortest path from a starting node to all other nodes in a graph with non-negative edge weights. How it works:
- Start from the source node.
- Keep track of the shortest distance to each node.
- Visit unvisited nodes always choosing the closest one.
- Update neighbors if a shorter path is found.
- Repeat until all nodes are visited.
It's like exploring a map where you always go to the nearest known place first, then look around again. Dijkstra's algorithm is used in: GPS navigation, Network routing, Game AI and Operations research.
1. Finding the shortest path - A * pathfinding

Two months ago I posted some interesting stuff I found: Shortest path. Let me explain, someone created a workbook that calculated the shortest path between a start cell and an end cell in a maze, and it did that using only formulas. Pretty amazing. The formulas were made from Dijkstra's Algorithm. I tried to create a larger maze but the workbook grew too large.
I then found the A * pathfinding algorithm and it is a lot easier for the computer to calculate. There is a great explanation of the A * pathfinding algorithm here: Introduction to A* Pathfinding.
Basically, there is an open list, a closed list and a final path. The open list contains cells that are being considered to find the final path. The closed list contains cells that we don't need to consider again.
They all contain coordinates or cells based on criteria. The criteria are:
- The distance to the END cell. (The distance to the END cell is calculated with the Manhattan distance method.
- The distance traveled from the start cell.
If the END cell is added to the open list, the closed list is finished calculating. Now it is time to find the final path. The final path is also found using the Manhattan distance method but it can only travel on cells in the closed list.
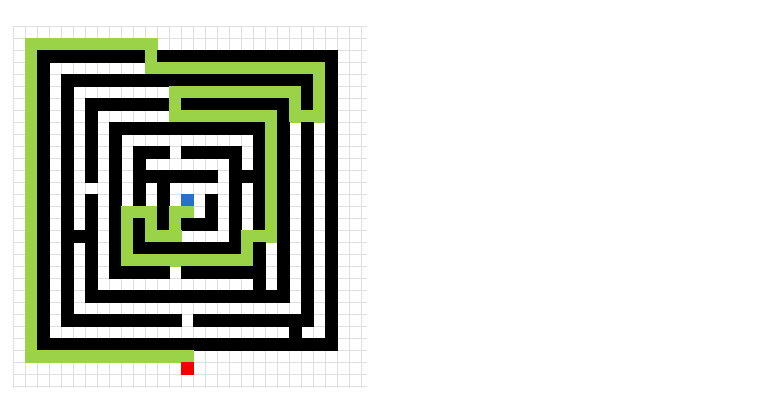
Here is an animated picture, it shows you how the macro works, simplified.
- The blue cell is the start cell
- The red cell is the end cell
- Gray cells are cells in the closed list.
- Green cells are the final path.
- Black cells are walls.
Here is a slightly more advanced "map".
This is a maze. I have removed the closed list cells to make the macro quicker.
VBA Code
'Name macro
Sub FindShortestPath1()
'Disable screen refresh for faster execution
Application.ScreenUpdating = False
'Dimension variables and their data types
Dim G() As Variant 'Stores the cost (G score) from the start node to a given node
Dim H() As Variant 'Stores the heuristic estimate (H score) from a given node to the end node (Manhattan distance)
Dim N() As Variant 'Stores the total estimated cost (N score = G + H) for a given node
Dim OL() As Variant 'Open List: Stores nodes to be evaluated ([0,i]=row, [1,i]=col)
Dim CL() As Variant 'Closed List: Stores nodes already evaluated ([0,i]=row, [1,i]=col)
Dim S() As Variant 'Start node coordinates ([0]=row, [1]=col)
Dim E() As Variant 'End node coordinates ([0]=row, [1]=col)
Dim W() As Variant 'Movement vectors for checking neighbors ([j,0]=row offset, [j,1]=col offset)
Dim Gv() As Variant 'Temporary storage for neighbor G scores during backtracking
Dim i As Single 'Loop counter variable
'Redimension coordinate and movement vector arrays
ReDim S(0 To 1) 'Stores Start row and column
ReDim E(0 To 1) 'Stores End row and column
ReDim W(0 To 3, 0 To 1) 'Stores 4 direction offsets (row, column)
ReDim OL(0 To 1, 0) 'Initialize Open List with space for 1 node (row, col)
ReDim CL(0 To 1, 0) 'Initialize Closed List with space for 1 node (row, col)
ReDim Gv(0 To 3) 'Stores G scores of 4 potential parent nodes during backtracking
'Save values in cell range specified in named range "Area" to variable Rng
Rng = Range("Area").Value
'Save the upper limit of rows (0-based index) from Rng variable to variable a
a = UBound(Rng, 1) - 1
'Save the upper limit of columns (0-based index) from Rng variable to variable b
b = UBound(Rng, 2) - 1
'Redimension grid-based variables (G, H, N scores) based on the size of the "Area" range
ReDim G(0 To a, 0 To b)
ReDim H(0 To a, 0 To b)
ReDim N(0 To a, 0 To b)
'--- Find Start (S) and End (E) points ---
'For ... next loop from 1 to the number of rows in Rng variable
For R = 1 To UBound(Rng, 1)
'For ... next loop from 1 to the number of columns in Rng variable
For C = 1 To UBound(Rng, 2)
'Check if cell Rng(r, C) is equal to "S" (start point)
If Rng(R, C) = "S" Then
'Save row index (0-based) in variable S position 0 (zero)
S(0) = R - 1
'Save column index (0-based) in variable S position 1
S(1) = C - 1
End If
'Check if cell Rng(r, C) is equal to "E" (end point)
If Rng(R, C) = "E" Then
'Save the row index (0-based) of the end point
E(0) = R - 1
'Save the column index (0-based) of the end point
E(1) = C - 1
End If
'Check if both S(0) and E(0) have been found
If S(0) <> "" And E(0) <> "" Then Exit For 'Exit inner loop if both found
Next C
'Check again if both S(0) and E(0) have been found to exit outer loop early
If S(0) <> "" And E(0) <> "" Then Exit For
Next R
'--- Initialize A* Algorithm ---
'Save starting row stored in S(0) to array variable CL (closed list) position 0,0
CL(0, 0) = S(0) 'row
'Save starting column stored in S(1) to array variable CL (closed list) position 1,0
CL(1, 0) = S(1) 'column
'Define the movement vectors (Neighbors: Up, Down, Left, Right)
'Save -1 (Up row offset) to array variable W position 0,0
W(0, 0) = -1
'Save 1 (Down row offset) to array variable W position 1,0
W(1, 0) = 1
'Save 0 (Left/Right row offset) to array variable W position 2,0
W(2, 0) = 0
'Save 0 (Up/Down row offset) to array variable W position 3,0
W(3, 0) = 0
'Save 0 (Up/Down column offset) to array variable W position 0,1
W(0, 1) = 0
'Save 0 (Left/Right column offset) to array variable W position 1,1
W(1, 1) = 0
'Save -1 (Left column offset) to array variable W position 2,1
W(2, 1) = -1
'Save 1 (Right column offset) to array variable W position 3,1
W(3, 1) = 1
'Initialize boolean variable Echk (End Check) to False - determines if the End node has been reached
Echk = False
'--- A* Search Loop ---
'Keep iterating until Echk is True (End node found)
Do Until Echk = True
'For ... next loop iterating through each node currently in the Closed List (CL)
For i = 0 To UBound(CL, 2)
'For ... next loop iterating through the 4 possible neighbor directions (using W array)
For j = 0 To 3
'Save boolean value False to variable chk - used to track if a neighbor is invalid or already processed
chk = False
'Calculate potential neighbor's row (tr) based on current node in CL and movement vector
tr = CL(0, i) + W(j, 0)
'Calculate potential neighbor's column (tc) based on current node in CL and movement vector
tc = CL(1, i) + W(j, 1)
'--- Check Neighbor Validity ---
'Check if the neighbor is outside the grid boundaries
If tr < 0 Or tc < 0 Or tr > UBound(Rng, 1) -1 Or tc > UBound(Rng, 2) -1 Then 'Adjusted bounds check to 0-based
'Mark neighbor as invalid if outside boundaries
chk = True
Else 'If within bounds, proceed with other checks
'Loop backwards through the Closed List (more efficient to find recent additions)
For k = UBound(CL, 2) To 0 Step -1
'Check if the neighbor (tr, tc) is already in the Closed List
If tr = CL(0, k) And tc = CL(1, k) Then
'Mark neighbor as invalid/processed if already in Closed List
chk = True
'Stop checking Closed List for this neighbor
Exit For
End If
Next k
'Check if the neighbor cell in the original grid (Rng) is an obstacle (marked as '1')
If Rng(tr + 1, tc + 1) = 1 Then chk = True 'Mark as invalid if it's an obstacle
'--- Check Open List ---
'Loop backwards through the Open List
For k = UBound(OL, 2) To 0 Step -1
'Check if the neighbor (tr, tc) is already in the Open List
If tr = OL(0, k) And tc = OL(1, k) Then
'Mark as checked (already considered), but may need cost update
chk = True
'Check if the path through the current node (CL(i)) is shorter than the existing path to this neighbor
If G(CL(0, i), CL(1, i)) + 1 < G(tr, tc) Then
'Update the G score (cost from start) for the neighbor via this new path
G(tr, tc) = G(CL(0, i), CL(1, i)) + 1
'Recalculate the H score (heuristic estimate to end - Manhattan distance)
H(tr, tc) = Abs(tr - E(0)) + Abs(tc - E(1))
'Update the N score (F score = G + H)
N(tr, tc) = G(tr, tc) + H(tr, tc)
End If
'Stop checking Open List for this neighbor
Exit For
End If
Next k
'--- Add Valid New Neighbor to Open List ---
'If the neighbor is valid (chk is False: not out of bounds, not obstacle, not in CL, not in OL)
If chk = False Then
'Add neighbor's row to the end of the Open List array
OL(0, UBound(OL, 2)) = tr
'Add neighbor's column to the end of the Open List array
OL(1, UBound(OL, 2)) = tc
'Expand the Open List array (Preserve existing data) to make space for the next potential node
ReDim Preserve OL(UBound(OL, 1), UBound(OL, 2) + 1)
'Calculate G score (cost from start = parent G + 1) for the new neighbor
G(tr, tc) = G(CL(0, i), CL(1, i)) + 1
'Calculate H score (heuristic - Manhattan distance to End) for the new neighbor
H(tr, tc) = Abs(tr - E(0)) + Abs(tc - E(1))
'Calculate N score (F score = G + H) for the new neighbor
N(tr, tc) = G(tr, tc) + H(tr, tc)
'Check if the newly added neighbor is the End point ("E")
If Rng(tr + 1, tc + 1) = "E" Then Echk = True 'Set the main loop flag to True if End is found
End If
End If
Next j ' Next neighbor direction
Next i ' Next node in Closed List
'--- Select Next Node to Process ---
'If the End point hasn't been reached in this iteration (Echk is False)
If Echk <> True Then
'Find the N score of the first valid node in the Open List to initialize the minimum check
Dim Nchk As Variant ' Variable to store the minimum N score found in OL
Nchk = "" ' Initialize Nchk
For i = LBound(OL, 2) To UBound(OL, 2) -1 ' Iterate up to the second to last element (last one is empty placeholder)
'Check if this slot in the Open List contains a valid node (row is not empty)
If OL(0, i) <> "" Then
'Initialize the minimum N score found so far with the first valid node's N score
Nchk = N(OL(0, i), OL(1, i))
'Stop searching once the first valid node is found and Nchk is initialized
Exit For
End If
Next i
'Iterate through the Open List again to find the node with the absolute minimum N score
For i = LBound(OL, 2) To UBound(OL, 2) - 1 ' Iterate up to the second to last element
'Check if this slot in the Open List contains a valid node (column is not empty)
If OL(1, i) <> "" Then ' Check using column coordinate
'If this node's N score is lower than the current minimum (Nchk) and is not empty
If N(OL(0, i), OL(1, i)) < Nchk And N(OL(0, i), OL(1, i)) <> "" Then
'Update the minimum N score (Nchk)
Nchk = N(OL(0, i), OL(1, i))
End If
End If
Next i
'Iterate through the Open List one more time to move the node(s) with the minimum N score to the Closed List
For i = LBound(OL, 2) To UBound(OL, 2) - 1 ' Iterate up to the second to last element
'Check if this slot contains a valid node
If OL(0, i) <> "" Then
'If this node has the minimum N score found (Nchk)
If N(OL(0, i), OL(1, i)) = Nchk Then
'Expand the Closed List array (Preserve existing data)
ReDim Preserve CL(UBound(CL, 1), UBound(CL, 2) + 1)
'Move the node's row from Open List to the end of the Closed List
CL(0, UBound(CL, 2)) = OL(0, i)
'Clear the node's row from the Open List (mark as moved)
OL(0, i) = ""
'Move the node's column from Open List to the end of the Closed List
CL(1, UBound(CL, 2)) = OL(1, i)
'Clear the node's column from the Open List (mark as moved)
OL(1, i) = ""
'Note: This finds *one* node with the minimum score per pass through OL.
'If multiple nodes have the same minimum score, only one might be moved per outer loop iteration, depending on Nchk initialization and loop order.
'A more robust implementation might collect all min N nodes first, then move them.
End If
End If
Next i
End If
Loop 'End of the main A* search loop (Do Until Echk = True)
'--- Backtrack to Reconstruct Path ---
'Initialize temporary row (tr) with the End point's row
tr = E(0)
'Initialize temporary column (tc) with the End point's column
tc = E(1)
'Initialize Schk (Start Check) flag to False - determines if Start node is reached during backtracking
Schk = False
'Loop until the Start point is reached (Schk = True)
Do Until Schk = True
'Reset temporary G score array for neighbors
For k = 0 To 3: Gv(k) = "": Next k
'Search backwards through the Closed List (contains nodes potentially on the shortest path)
'This nested loop structure is inefficient for finding the parent. It iterates through the entire Closed List for each step.
'A better way would be to store parent pointers during the A* search.
For i = UBound(CL, 2) To 0 Step -1 ' Check nodes in Closed List
' Check potential parent BELOW current node (tr, tc)
If CL(0, i) = (tr + 1) And CL(1, i) = tc _
And (Rng(tr + 1 + 1, tc + 1) <> "W" And Rng(tr + 1 + 1, tc + 1) <> "1") Then ' Check if valid and not already path/obstacle
Gv(0) = G(tr + 1, tc) ' Store G score of node below
End If
' Check potential parent RIGHT of current node (tr, tc)
If CL(0, i) = tr And CL(1, i) = (tc + 1) _
And (Rng(tr + 1, tc + 1 + 1) <> "W" And Rng(tr + 1, tc + 1 + 1) <> "1") Then ' Check if valid and not already path/obstacle
Gv(1) = G(tr, tc + 1) ' Store G score of node right
End If
' Check potential parent ABOVE current node (tr, tc)
If CL(0, i) = (tr - 1) And CL(1, i) = tc _
And (Rng(tr - 1 + 1, tc + 1) <> "W" And Rng(tr - 1 + 1, tc + 1) <> "1") Then ' Check if valid and not already path/obstacle
Gv(2) = G(tr - 1, tc) ' Store G score of node above
End If
' Check potential parent LEFT of current node (tr, tc)
If CL(0, i) = tr And CL(1, i) = (tc - 1) _
And (Rng(tr + 1, tc - 1 + 1) <> "W" And Rng(tr + 1, tc - 1 + 1) <> "1") Then ' Check if valid and not already path/obstacle
Gv(3) = G(tr, tc - 1) ' Store G score of node left
End If
Next i ' Finished checking all nodes in CL for potential parents of (tr, tc)
'--- Find Parent Node (Lowest G Score Neighbor) ---
Dim Nf As Variant ' Stores the minimum G score found among neighbors
Nf = "" ' Initialize Nf
'Initialize Nf with the first valid G score found in Gv
For j = 0 To 3
If Gv(j) <> "" Then
Nf = Gv(j)
Exit For ' Exit after finding the first one
End If
Next j
'Find the actual minimum G score among the valid neighbors stored in Gv
For j = 0 To 3
If Gv(j) < Nf And Gv(j) <> "" Then Nf = Gv(j) ' Update Nf if a smaller G score is found
Next j
'--- Mark Path and Move to Parent ---
'Temporarily enable screen updating to show path drawing step-by-step (can slow down significantly for large grids)
'Application.ScreenUpdating = True ' Usually keep this off until the end
'Select the neighbor based on the minimum G score (Nf) found - this identifies the parent node
Select Case Nf
Case Gv(0) ' If the node below was the parent (lowest G score)
tr = tr + 1 ' Move current position (tr) down to the parent node
'Check if not Start or End before marking - Optional but good practice
If Rng(tr + 1, tc + 1) <> "S" And Rng(tr + 1, tc + 1) <> "E" Then
Range("Area").Cells(tr + 1, tc + 1) = "W" ' Mark the parent cell as path ('W') on the worksheet
Rng(tr + 1, tc + 1) = "W" ' Also mark it in the internal Rng array to avoid conflicts in checks
End If
Case Gv(1) ' If the node right was the parent
tc = tc + 1 ' Move current position (tc) right to the parent node
If Rng(tr + 1, tc + 1) <> "S" And Rng(tr + 1, tc + 1) <> "E" Then
Range("Area").Cells(tr + 1, tc + 1) = "W"
Rng(tr + 1, tc + 1) = "W"
End If
Case Gv(2) ' If the node above was the parent
tr = tr - 1 ' Move current position (tr) up to the parent node
If Rng(tr + 1, tc + 1) <> "S" And Rng(tr + 1, tc + 1) <> "E" Then
Range("Area").Cells(tr + 1, tc + 1) = "W"
Rng(tr + 1, tc + 1) = "W"
End If
Case Gv(3) ' If the node left was the parent
tc = tc - 1 ' Move current position (tc) left to the parent node
If Rng(tr + 1, tc + 1) <> "S" And Rng(tr + 1, tc + 1) <> "E" Then
Range("Area").Cells(tr + 1, tc + 1) = "W"
Rng(tr + 1, tc + 1) = "W"
End If
End Select
'Disable screen updating again after marking the cell
'Application.ScreenUpdating = False ' Usually keep this off until the end
'--- Check if Start Reached ---
'Check if any neighbor of the *current* node (which is now the parent found via Select Case) is the Start point "S".
'This check seems slightly off - it should ideally check if tr, tc *is* the start node S(0), S(1) after moving.
'Current check: If any NEIGHBOR of the node we just moved *to* is 'S'. This will stop one step early.
' A better check would be: If tr = S(0) And tc = S(1) Then Schk = True
If Rng(tr + 1 + 1, tc + 1) = "S" _
Or Rng(tr + 1, tc + 1 + 1) = "S" _
Or Rng(tr - 1 + 1, tc + 1) = "S" _
Or Rng(tr + 1, tc - 1 + 1) = "S" Then
Schk = True ' Set flag to True, backtracking is complete.
End If
'Alternative check: Directly compare current position to Start position
If tr = S(0) And tc = S(1) Then Schk = True
Loop 'End of the backtracking loop (Do Until Schk = True)
'Enable screen updating to show the final result with the path marked
Application.ScreenUpdating = True
'Macro finished
End Sub
Explanation of the Macro (A* Search Algorithm)
This VBA macro implements the A* (A-star) search algorithm to find the shortest path between a start point ("S") and an end point ("E") within a grid defined by the named range "Area" in an Excel sheet. Obstacles are represented by cells containing the value 1.
Here's a breakdown of the steps:
- Initialization:
- Turns off screen updating for speed.
- Declares variables:
- G, H, N: Arrays to store A* scores for each cell in the grid (G=cost from start, H=heuristic estimate to end, N=G+H).
- OL (Open List): Stores nodes (cells) that are candidates for exploration.
- CL (Closed List): Stores nodes that have already been explored.
- S, E: Store coordinates of Start and End points.
- W: Stores movement offsets (up, down, left, right).
- Rng: Stores the grid data from the "Area" range.
- Reads the grid data into the Rng array.
- Finds the row/column indices of "S" and "E" within the grid.
- Initializes A*: Adds the Start node "S" to the Closed List (CL). Sets up the W movement vectors.
- A* Search Loop (Do Until Echk = True):
- This is the core of the algorithm. It continues until the End node "E" is found (Echk = True).
- Node Expansion: It iterates through the nodes currently in the Closed List (CL). For each node, it examines its neighbors (up, down, left, right).
- Neighbor Evaluation: For each neighbor:
- It checks if the neighbor is valid (within grid boundaries, not an obstacle '1', not already in the Closed List).
- If neighbor is in Open List: It checks if the path through the current node is shorter than the previously known path to that neighbor. If so, it updates the neighbor's G and N scores in the OL.
- If neighbor is valid and not in Open List: It calculates the G, H, and N scores for the neighbor and adds it to the Open List (OL). It also checks if this neighbor is the End node "E"; if so, it sets Echk to True to signal the end of the search phase.
- Select Next Node: After evaluating neighbors for all nodes currently in CL, if the End node hasn't been found:
- It finds the node in the Open List (OL) with the lowest N score (the most promising node to explore next).
- It moves this selected node from the Open List (OL) to the Closed List (CL).
- Path Reconstruction (Backtracking - Do Until Schk = True):
- Once the End node is found (Echk = True), this loop reconstructs the path backwards from End to Start.
- It starts at the End node (E).
- In each step, it looks at the neighbors of the current node that are present in the Closed List.
- It identifies the neighbor with the lowest G score. This neighbor is the "parent" node in the shortest path found by A*.
- It marks the parent node on the worksheet with "W" (representing the Way/Path).
- It moves the current position to this parent node.
- It repeats this process until the Start node "S" is reached (Schk = True).
- Finalization:
- Turns screen updating back on to display the grid with the path marked ("W").
2. Optimize pick path in a warehouse
As you probably already are aware of I have shown you earlier a vba macro I made that finds the shortest path between two points. There are obstacles between these two points to make it more difficult.

The problem with that macro is that it could only show a path that moves up, down, left or right. So I had to change it so it can move in eight directions.
Instead of using 6 movements it now uses 3 movements, it can now go diagonal from A to B. This is more realistic, of course.
Calculating all possible paths between 15 locations
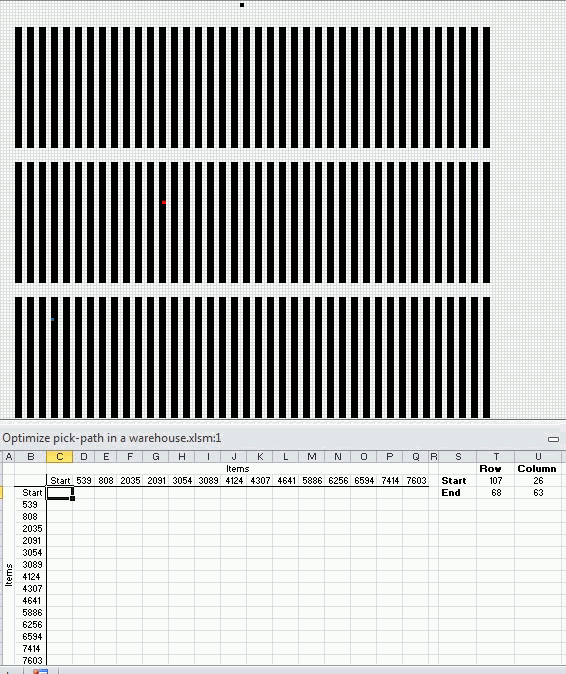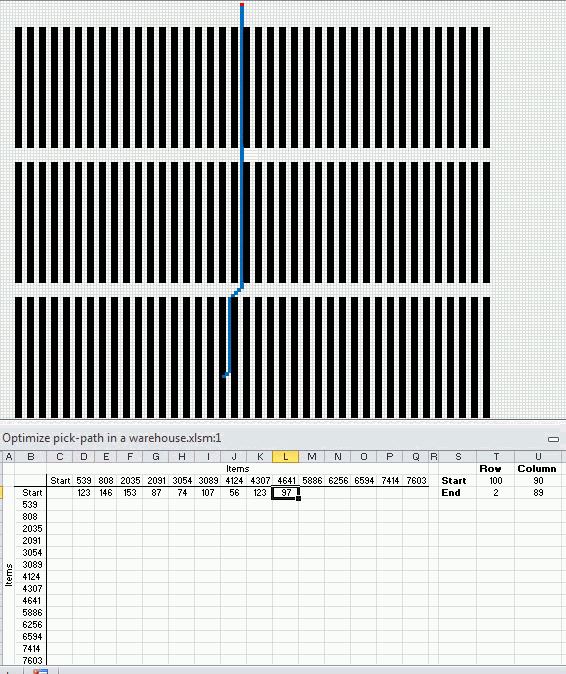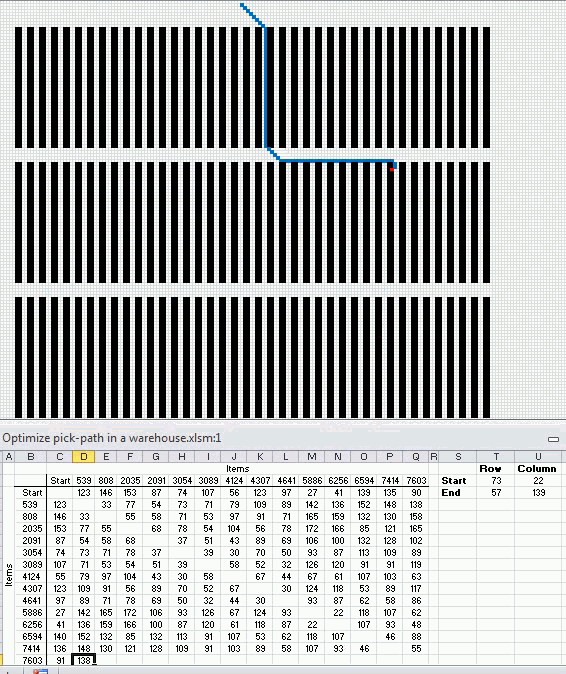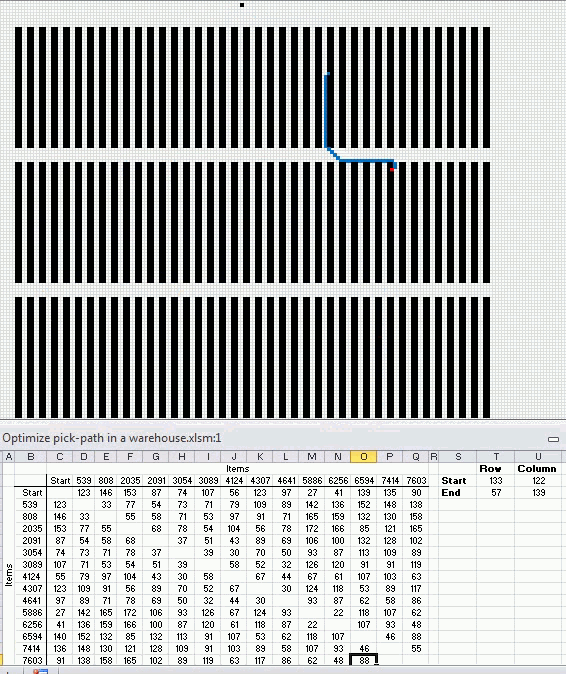
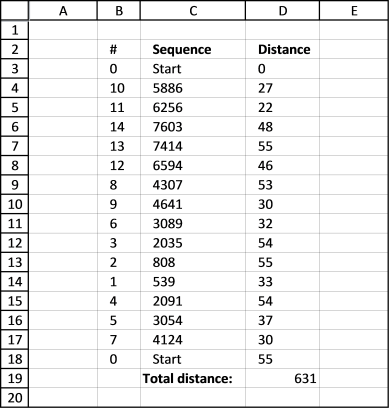
The following animated picture shows you 9600 storage locations, named item 1 to 9600. Each black dot is a storage location in this warehouse.
There is a start point almost at the top of this picture. I have chosen 14 random locations and the macro shows the shortest path and calculates the distance in the table at the bottom of this picture.
Find the shortest pick path
Now that we have all distances between 15 locations we can use the Excel Solver to find the shortest path. First we need to setup a sheet.
Formula in cell C4:
=INDEX(Items!$H$4:$H$17, MATCH('Optimize total path'!B4, Items!$G$4:$G$17, 0))
Formula in cell D4:
=INDEX(Paths!$C$3:$Q$17, MATCH('Optimize total path'!C3, Paths!$B$3:$B$17, 0), MATCH('Optimize total path'!C4, Paths!$C$2:$Q$2, 0))
Formula in cell D19:
=SUM(D3:D18)
Now it is time for the excel solver to find the optimal path. If you need more detailed instructions, check out this page: Travelling Salesman Problem in Excel Solver
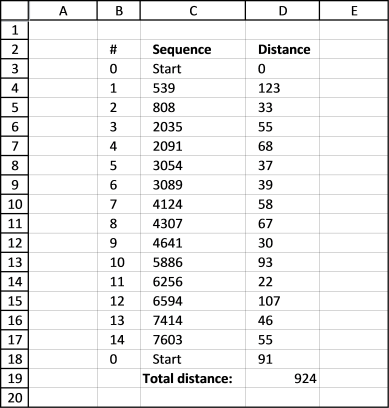
After a few minutes this sequence is shown with the shortest total distance.
Optimal path
Here is the shortest path. It begins with the start point almost at the top and goes through all 14 storage locations and then back to start point.
Read more interesting posts:
- A quicker A * pathfinding algorithm
- Finding the shortest path – A * pathfinding
- Build a maze
- Solve a maze
- Identify numbers in sum using solver
- Excel udf: Find numbers in sum
Get excel *.xlsm file
Optimize-pick-path-in-a-warehouse1.xlsm
3. A quicker A * pathfinding algorithm
3 weeks ago I showed you a A* pathfinding algorithm. It was extremely slow and sluggish and I have now made it smaller and faster, much faster.
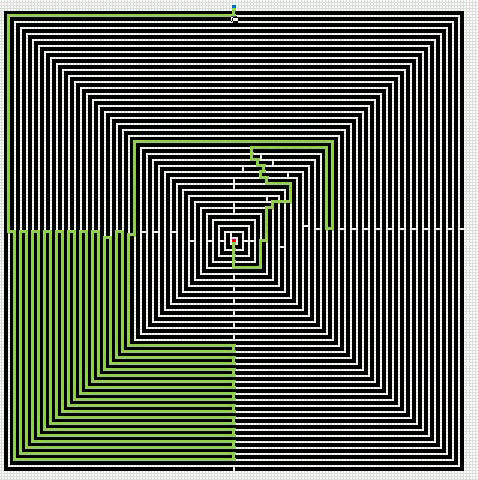
Here is an animated gif showing you a grid 255 * 255 cells. The blue cell is the start cell and it is located almost at the top center. The red cell is the end cell and it is in the middle of the maze. I have walls in this grid, if a cell contains value 1 it is colored black with conditional formatting.
The animation shows me deleting walls and the subroutine finds a new shorter path, highlighted green.
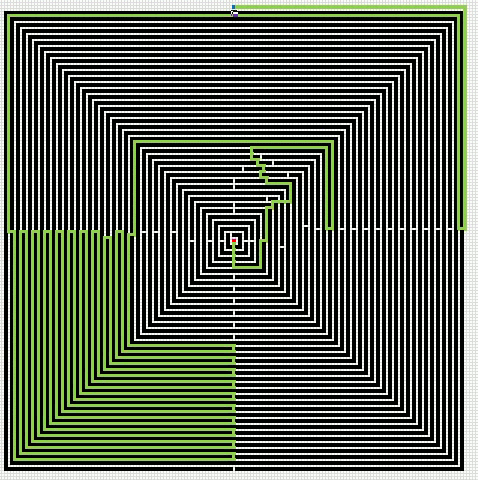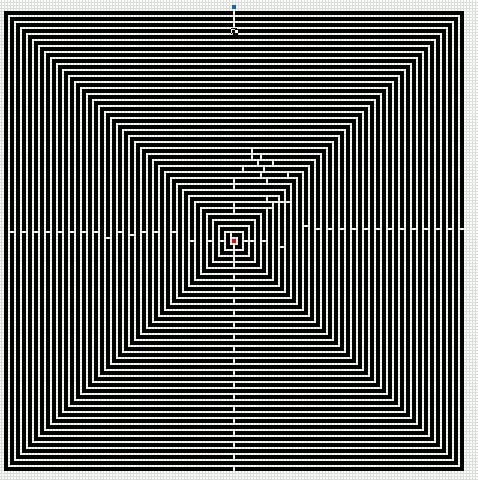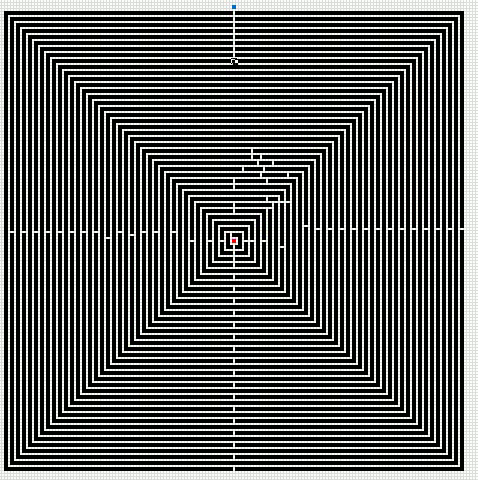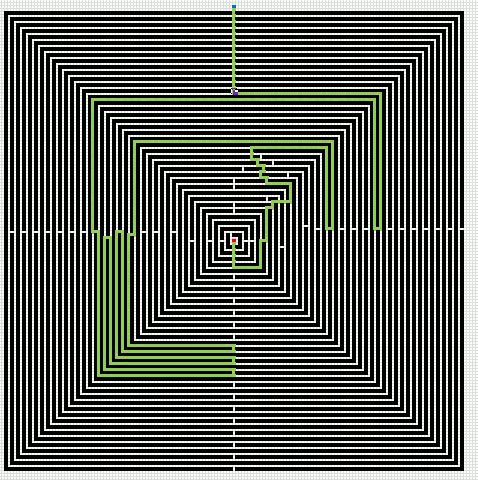
An Event procedure removes the old path and calculates the new path if a cell is changed on this sheet. If you want to remove the even procedure, press with right mouse button on on sheet1. Press with left mouse button on "View Code..". Comment line 3:
Private Sub Worksheet_Change(ByVal Target As Range) Application.EnableEvents = False 'Call FindShortestPath1 Application.EnableEvents = True End Sub
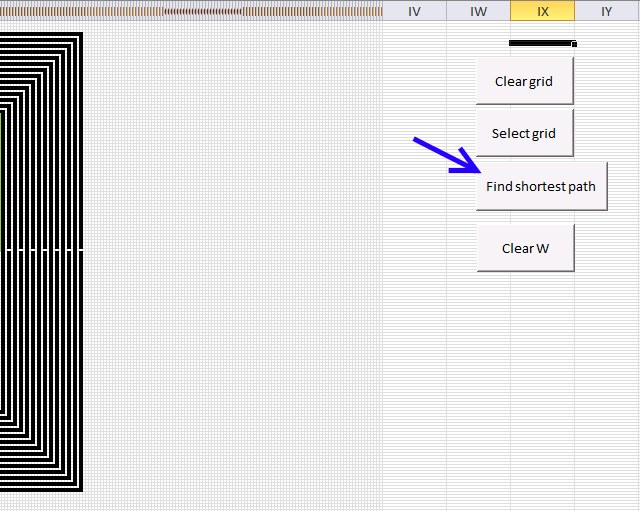
You can start the path optimization manually by press with left mouse button oning the button "Find shortest path".
Button "ClearW" clears the path.
Button "Clear grid" clears everything, start and end point, walls and path.
VBA code
Sub FindShortestPath1()
'This macro shows only the final path
'The defined named range "Area" tells this mcro which cell range to use
Application.ScreenUpdating = False
Dim G() As Variant
Dim H() As Variant
Dim N() As Variant
Dim O() As Variant
Dim C() As Variant
Dim OL() As Variant
Dim CL() As Variant
Dim S() As Variant
Dim E() As Variant
Dim W() As Variant
Dim Gv() As Variant
Dim i As Single
ReDim S(0 To 1)
ReDim E(0 To 1)
ReDim W(0 To 3, 0 To 1)
ReDim OL(0 To 1, 0)
ReDim CL(0 To 1, 0)
ReDim Gv(0 To 3)
Call ClearW
Rng = Range("Area").Value
a = UBound(Rng, 1) - 1
b = UBound(Rng, 2) - 1
ReDim G(0 To a, 0 To b)
ReDim H(0 To a, 0 To b)
ReDim N(0 To a, 0 To b)
ReDim O(0 To a, 0 To b)
ReDim C(0 To a, 0 To b)
'Find start and end coordinates in cell range
For Ri = 1 To UBound(Rng, 1)
For Ci = 1 To UBound(Rng, 2)
If Rng(Ri, Ci) = "S" Then
S(0) = Ri - 1
S(1) = Ci - 1
End If
If Rng(Ri, Ci) = "E" Then
E(0) = Ri - 1
E(1) = Ci - 1
End If
If S(0) <> "" And E(0) <> "" Then Exit For
Next Ci
Next Ri
'Add S to closed list
CL(0, 0) = S(0) 'row
CL(1, 0) = S(1) 'column
'Add values to closed list
W(0, 0) = -1
W(1, 0) = 1
W(2, 0) = 0
W(3, 0) = 0
W(0, 1) = 0
W(1, 1) = 0
W(2, 1) = -1
W(3, 1) = 1
Echk = False
Do Until Echk = True
For i = 0 To UBound(CL, 2)
For j = 0 To 3
chk = False
tr = CL(0, i) + W(j, 0)
tc = CL(1, i) + W(j, 1)
'Check if coordinates are less than 1 or larger than 255
If tr < 0 Or tc < 0 Or tr > UBound(Rng, 1) - 1 Or tc > UBound(Rng, 2) - 1 Then
chk = True
Else
'Check if new coordinates already exist on the closed list
On Error Resume Next
If C(tr, tc) = "C" Then chk = True
If Err <> 0 Then
MsgBox tr & " " & tc
Exit Sub
End If
'Check if coordinate is a wall
If Rng(tr + 1, tc + 1) = 1 Then chk = True
If O(tr, tc) = "O" Then
chk = True
'Calculate G, H and N
If G(CL(0, i), CL(1, i)) + 1 < G(tr, tc) Then
G(tr, tc) = G(CL(0, i), CL(1, i)) + 1
H(tr, tc) = Abs(tr - E(0)) + Abs(tc - E(1))
N(tr, tc) = G(tr, tc) + H(tr, tc)
End If
End If
'Check if coordinate is NOT on the Open list or Closed list or is a wall
If chk = False Then
'Add coordinates to open list
O(tr, tc) = "O"
OL(0, UBound(OL, 2)) = tr
OL(1, UBound(OL, 2)) = tc
ReDim Preserve OL(UBound(OL, 1), UBound(OL, 2) + 1)
'Calculate G, H and N
G(tr, tc) = G(CL(0, i), CL(1, i)) + 1
H(tr, tc) = Abs(tr - E(0)) + Abs(tc - E(1))
N(tr, tc) = G(tr, tc) + H(tr, tc)
'Check if cell is End
If Rng(tr + 1, tc + 1) = "E" Then Echk = True
End If
End If
Next j
Next i
'Remove all values in closed list
ReDim CL(0 To 1, 0)
'Find cell(s) in the open list that has the smallest N and add those to the closed list
'Find a value for Nchk
If Echk <> True Then
For i = LBound(OL, 2) To UBound(OL, 2)
If OL(0, i) <> "" Then
Nchk = N(OL(0, i), OL(1, i))
Exit For
End If
Next i
'Find smallest N
For i = LBound(OL, 2) To UBound(OL, 2)
If OL(1, i) <> "" Then
If N(OL(0, i), OL(1, i)) < Nchk And N(OL(0, i), OL(1, i)) <> "" Then
Nchk = N(OL(0, i), OL(1, i))
End If
End If
Next i
'Add cell(s) from open list that has the lowest N, to closed list
Eend = False
For i = LBound(OL, 2) To UBound(OL, 2)
If i <= UBound(OL, 2) Then
On Error GoTo 0
If OL(0, i) <> "" Then
If N(OL(0, i), OL(1, i)) = Nchk Then
Eend = True
If CL(0, 0) <> "" Then ReDim Preserve CL(UBound(CL, 1), UBound(CL, 2) + 1)
C(OL(0, i), OL(1, i)) = "C"
CL(0, UBound(CL, 2)) = OL(0, i)
OL(0, i) = ""
CL(1, UBound(CL, 2)) = OL(1, i)
OL(1, i) = ""
'Remove blank values in open list
For j = i To UBound(OL, 2) - 1
OL(0, j) = OL(0, j + 1)
OL(1, j) = OL(1, j + 1)
Next j
ReDim Preserve OL(UBound(OL, 1), UBound(OL, 2) - 1)
End If
End If
End If
Next i
If Eend = False Then
MsgBox "There is no free path"
Exit Sub
End If
End If
Loop
'Build final path
tr = E(0)
tc = E(1)
Schk = False
Do Until Schk = True
If C(tr + 1, tc) = "C" _
And (Rng(tr + 2, tc + 1) <> "W" _
And Rng(tr + 2, tc + 1) <> "1") _
Then Gv(0) = G(tr + 1, tc)
If C(tr, tc + 1) = "C" _
And (Rng(tr + 1, tc + 2) <> "W" _
And Rng(tr + 1, tc + 2) <> "1") _
Then Gv(1) = G(tr, tc + 1)
If C(tr - 1, tc) = "C" _
And (Rng(tr, tc + 1) <> "W" _
And Rng(tr, tc + 1) <> "1") _
Then Gv(2) = G(tr - 1, tc)
If C(tr, tc - 1) = "C" _
And (Rng(tr + 1, tc) <> "W" _
And Rng(tr + 1, tc) <> "1") _
Then Gv(3) = G(tr, tc - 1)
'Find smallest G
For j = 0 To 3
If Gv(j) <> "" Then Nf = Gv(j)
Next j
For j = 0 To 3
If Gv(j) < Nf And Gv(j) <> "" Then Nf = Gv(j)
Next j
Select Case Nf
Case Gv(0)
tr = tr + 1
Rng(tr + 1, tc + 1) = "W"
Case Gv(1)
tc = tc + 1
Rng(tr + 1, tc + 1) = "W"
Case Gv(2)
tr = tr - 1
Rng(tr + 1, tc + 1) = "W"
Case Gv(3)
tc = tc - 1
Rng(tr + 1, tc + 1) = "W"
End Select
If Rng(tr + 2, tc + 1) = "S" _
Or Rng(tr + 1, tc + 2) = "S" _
Or Rng(tr, tc + 1) = "S" _
Or Rng(tr + 1, tc) = "S" Then Schk = True
Loop
Range("Area") = Rng
Application.ScreenUpdating = True
End Sub
Get Excel *.xlsm file
For next statement category
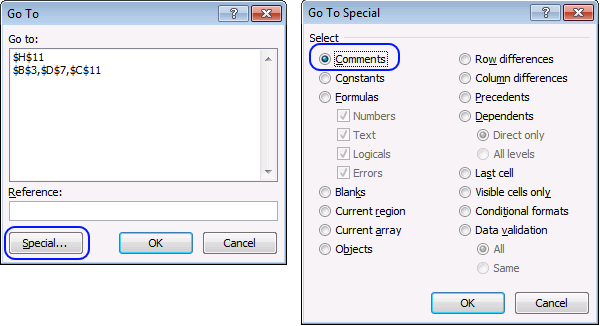
Did you know that you can select all cells containing comments in the current sheet? Press F5, press with left […]
Pathfinding category
More than 1300 Excel formulasExcel categories
3 Responses to “Finding the shortest path – A * pathfinding”
Leave a Reply
How to comment
How to add a formula to your comment
<code>Insert your formula here.</code>
Convert less than and larger than signs
Use html character entities instead of less than and larger than signs.
< becomes < and > becomes >
How to add VBA code to your comment
[vb 1="vbnet" language=","]
Put your VBA code here.
[/vb]
How to add a picture to your comment:
Upload picture to postimage.org or imgur
Paste image link to your comment.
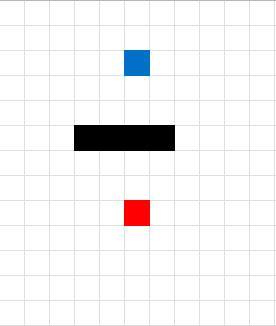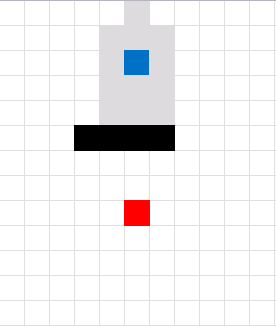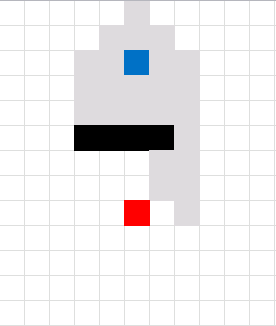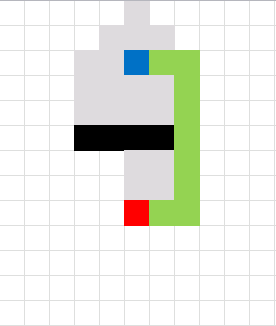



impressive!
Torstein,
Thank you but the idea is not mine. The A * algorithm is used in many computer games.
It is a very interesting technique and I believe I can make my macro run a lot quicker with some minor changes.
[UPDATE]
A quicker A * pathfinding algorithm
Nice explanation :) Here are some other visualizations with extra info, helping to better understand A* (along with forkeable examples): https://thewalnut.io/visualizer/visualize/7/6/