How to use the PV function
What is the PV function?
The PV function calculates the net present value for an investment or loan. PV stands for present value.
What's on this webpage
1. Introduction
What is an investment?
An investment is an asset or business acquired with the goal of generating income or appreciation, the purpose is to grow the money over time.
What are periods?
A payment period is the length of time between payments made on a loan or investment. For example, a loan with monthly payments the payment period would be one month. A loan with quarterly payments the payment period would be three months.
What is present value?
The present value is the initial amount that will earn interest/dividend.
What is future value?
The compounded amount after the calculated periods based on the given rate. It measures what a current capital (present value) amount will be worth at a designated future date.
What are periodic constant payments?
Periodic constant payments are payments that are made at regular intervals such as monthly, quarterly, or yearly and have the same amount each time.
What is a constant interest rate?
A fixed interest rate is an interest rate that remains the same throughout the term of a loan or an investment.
What is the number of compounding periods per year?
The number of compounding periods per year refers to how often interest is compounded annually on an investment or loan.
Some common compounding periods:
- Annually - 1 compounding period per year
- Semiannually - 2 compounding periods per year
- Quarterly - 4 compounding periods per year
- Monthly - 12 compounding periods per year
- Weekly - 52 compounding periods per year
- Daily - 365 compounding periods per year
Related functions
| Function | Description |
|---|---|
| RATE(nper, pmt, pv, [fv], [type]) | Returns the interest rate per period of an annuity |
| PV(rate, nper, pmt, [fv], [type]) | Returns the present value of an investment. |
| FV(rate, nper, pmt, [pv], [type]) | Returns the future value of an investment. |
| PDURATION(rate, pv, fv) | Returns the periods needed for an investment to reach a future value. |
What is the math formula behind this function?
The math formula to calculate the present value is:
PV = [fv]/((1 + rate)^nper)
- PV = The present value of the amount to be paid in the future
- rate: The periodic interest rate (decimal value)
- nper: The total number of payment periods
- fv: The future value or remaining balance after the final payment
2. Syntax
PV(rate, nper, pmt, [fv], [type])
| rate | Required. The interest rate per period. If nper is years then the interest rate is per year. Divide the interest rate with 12 if you use months in the nper argument. |
| nper | Required. The total number of payment periods in an annuity. |
| pmt | Required. The payment amount per period. Interest and principal is often included in this amount but not other fees or taxes. The pmt argument is not used if you use the [fv] argument. |
| [fv] | Optional. The future value. |
| [type] | Optional. The number 0 or 1 and indicates when payments are due. |
3. Example 1

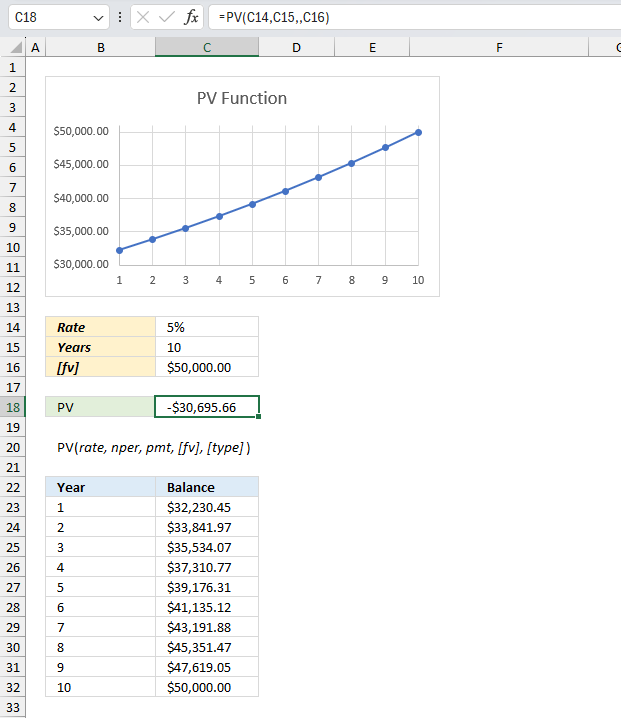
You want to save $50,000 for a down payment on a house in 10 years. If you can earn an annual interest rate of 5%, how much do you need to invest initially to reach your goal?
The image above shows a chart that displays the present value calculation over 10 periods using a future value of $50,000 and a rate of 5%.
The arguments provided are:
- Rate: 5% (0.05)
- Years: 10
- [fv]: $50,000.00
Formula in cell C18:
The formula in cell C18 calculates the present value equal to -$30,695.66 based on an interest rate of 5%, nper equal to 10, and the [fv] (future value) argument is $50,000.
The table below the arguments shows the year-by-year calculation of the present value using the PV function in Excel. It displays the balance for each year from 1 to 10.
The math formula to calculate the present value is:
PV = [fv]/((1 + rate)^nper)
- PV = The present value of the amount to be paid in the future
- rate: The periodic interest rate (e.g., 5% or 0.05)
- nper: The total number of payment periods (e.g., 10 for 10 years)
- fv: The future value or remaining balance after the final payment (50,000)
50000/((1+0.05)^10)
becomes
50000/1.62889462677744 equals 30695.66 which is the same as in cell C18.
4. Example 2
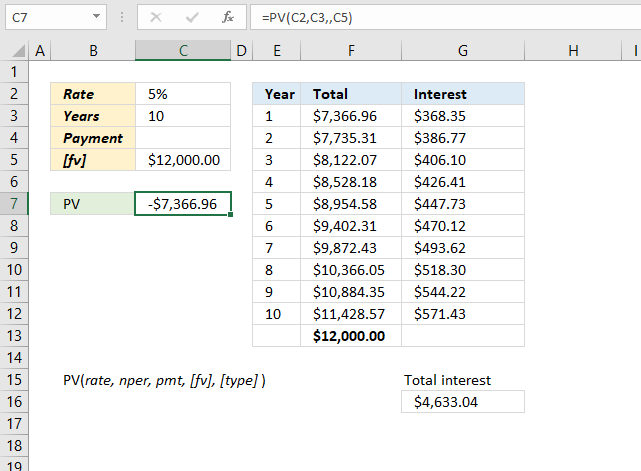
You want to save $12,000 for a vehicle in 10 years. If you can earn an annual interest rate of 5%, how much do you need to invest initially to reach your goal?
The image above demonstrates how to use the PV function when you want to know the amount needed for an investment when the interest rate is specified, and the number of periods are given.
The arguments provided are:
- Rate: 5% (0.05)
- Years: 10
- [fv]: $12,000
Formula in cell C7:
Note that the pmt argument can be empty when you specify the fv (future value) argument in the PV function.
The table, shown in the image above, displays the start amount and the interest for each period. The total accumulates the interest (column F) and the fv (future value) is reached after the given period. The table is not needed for the calculation, it is only there to show that the numbers add up and are correct.
See cell F13, it is equal to the future value in cell C5.
Formula in cell F3:
Copy cell F3 and paste cells below.
Formula in cell G3:
Copy cell G3 and paste cells below.
The math formula to calculate the present value is:
PV = [fv]/((1 + rate)^nper)
- PV = The present value of the amount to be paid in the future
- rate: The periodic interest rate (e.g., 5% or 0.05)
- nper: The total number of payment periods (e.g., 10 for 10 years)
- fv: The future value or remaining balance after the final payment (12,000)
12000/((1+0.05)^10)
becomes
12000/1.62889462677744 equals 7,366.96 which is the same as in cell C18.
5. Example 3
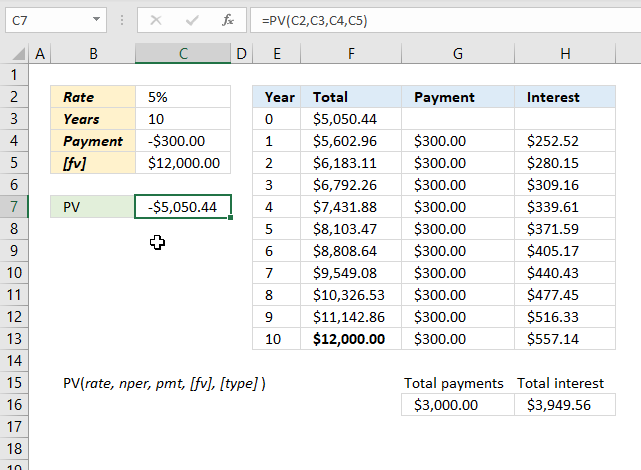
An small company wants to save $12,000 for a machine in 10 years. If the annual interest rate is 5% and the yearly payment is $300. How much is needed to invest initially to reach the amount?
The image above shows what amount is needed if you save x amount for each period to reach a future value [fv) given a constant interest rate.
The arguments provided are:
- Rate: 5% (0.05)
- Years (nper) = 10
- Payment (pmt) = -$300
- Future value [fv]: $12,000
Formula in cell C7:
The table in cell range E2:H13 shows that the numbers add up to the future value, specified in cell C5, after the given time of periods based on a constant interest rate.
The table is not needed to calculate the present value of the investment, the PV function is all that is needed.
Formula in cell F3:
Copy cell F3 and paste to cells below as far as needed.
Formula in cell G4:G13:
Formula in cell H4:
Copy cell H4 and paste to cells below as far as needed.
Useful links
PV function - Microsoft support
Excel Formula Coach - find the present value of a loan
Present Value Calculator
Functions in 'Financial' category
The PV Function function is one of 27 functions in the 'Financial' category.
How to comment
How to add a formula to your comment
<code>Insert your formula here.</code>
Convert less than and larger than signs
Use html character entities instead of less than and larger than signs.
< becomes < and > becomes >
How to add VBA code to your comment
[vb 1="vbnet" language=","]
Put your VBA code here.
[/vb]
How to add a picture to your comment:
Upload picture to postimage.org or imgur
Paste image link to your comment.
Contact Oscar
You can contact me through this contact form