How to use the EFFECT function
What is the EFFECT function?
The EFFECT function calculates the effective annual interest rate, given the nominal annual interest rate and the number of compounding periods per year.
Table of Contents
1. Introduction
What is the effective annual interest rate?
The effective annual interest rate is the actual annual interest rate earned on an investment after accounting for compounding frequency.
What is the nominal annual interest rate?
The nominal annual interest rate, also known as the stated annual interest rate, is the rate of interest quoted on an investment or loan without accounting for compounding.
It does not consider compounding periods within the year, often stated as "per annum" or "per year". If interest compounds during the year, the effective annual rate will differ from the nominal rate.
What is the number of compounding periods per year?
The number of compounding periods per year refers to how often interest is compounded annually on an investment or loan.
Some common compounding periods:
- Annually - 1 compounding period per year
- Semiannually - 2 compounding periods per year
- Quarterly - 4 compounding periods per year
- Monthly - 12 compounding periods per year
- Weekly - 52 compounding periods per year
- Daily - 365 compounding periods per year
The number of compounding periods impacts the effective annual interest rate. More frequent compounding results in higher effective rates.
What is the difference between the NOMINAL function and the EFFECT function?
NOMINAL function calculates the nominal annual interest rate based on the effective rate without taking compounding into account.
EFFECT function calculates the effective annual interest rate based on the nominal rate factoring in the effect of compounding periods within the year.
Knowing both rates helps properly compare interest costs and earnings on loans and investments.
What is the nominal annual interest rate?
The nominal annual interest rate, also known as the stated annual interest rate, is the rate of interest quoted on an investment or loan without accounting for compounding.
It does not consider compounding periods within the year, often stated as "per annum" or "per year". If interest compounds during the year, the effective annual rate will differ from the nominal rate.
How is the EFFECT function calculated?
The EFFECT function calculates the effective annual interest rate using the following formula:
=(1+n/p)p - 1
n - nominal rate
p - number of compounding periods per year.
For example: Annually: 10% interest compounded annually: Effective rate = 10%
Monthly: 10% interest compounded monthly: Effective rate = (1 + 0.10/12)12 - 1 = 10.47%
Daily: 10% interest compounded daily: Effective rate = (1 + 0.10/365)^365 - 1 = 10.52%
The effective annual rate will exceed the stated rate when compounding within a year. The effective rate translates the earned interest into the true annual return rate. It is higher than the periodic rate with frequent compounding.
2. Syntax
EFFECT(nominal_rate, npery)
| nominal_rate | Required. The nominal interest rate. |
| npery | Required. The number of compounding periods per year. |
3. Example 1

A savings account offers an annual interest rate of 4.5%, compounded quarterly. What is the effective annual interest rate for this account?
Arguments:
- nominal_rate: This is the nominal annual interest rate. Use a decimal value, not a percentage.
- npery: This is the number of compounding periods per year. This must be a positive integer.
An annual interest rate of 4.5% compounded quarterly, the nominal_rate would be 0.045 (4.5% expressed as a decimal), and the npery would be 4 (4 quarters in a year).
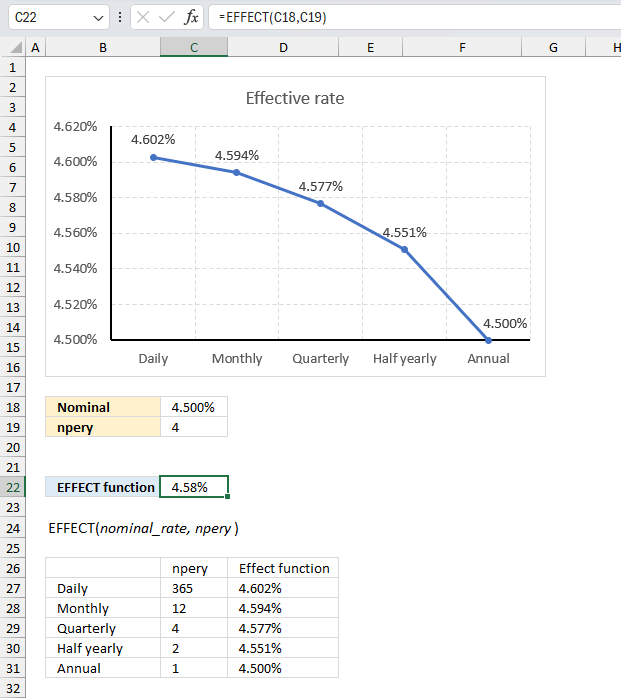
Formula in cell C22:
The formula in cell C22 returns 4.58% which represents the effective annual interest rate based of 4.5% compounded quarterly.
The chart above shows the effective annual interest rate for different compounding periods, they are daily, monthly, quarterly, half yearly, and yearly. For an annual interest rate of 4.5% the effective interest rate for:
- daily compounding is 4.602%
- monthly compounding is 4.594%
- quarterly compounding is 4.577%
- half yearly is 4.551%
- annual is 4.5%
The EFFECT function calculates the effective annual interest rate using the following formula:
Effective Annual Rate = (1 + nominal_rate/npery)^npery - 1
(1 + 0.045/4)^4 - 1 is approximately 0.04577 or 4.577% This value matches the calculated value in cell C22.
4. Example 2
An investment opportunity promises a nominal annual return of 8%, compounded semi-annually. Calculate the effective annual interest rate for this investment?
Arguments:
- nominal_rate: This is the nominal annual interest rate. Use a decimal value, not a percentage.
- npery: This is the number of compounding periods per year. This must be a positive integer.
An annual interest rate of 8% compounded half yearly or semi-annually, the nominal_rate would be 0.08 (8% expressed as a decimal), and the npery would be 2 (2 halves in a year).
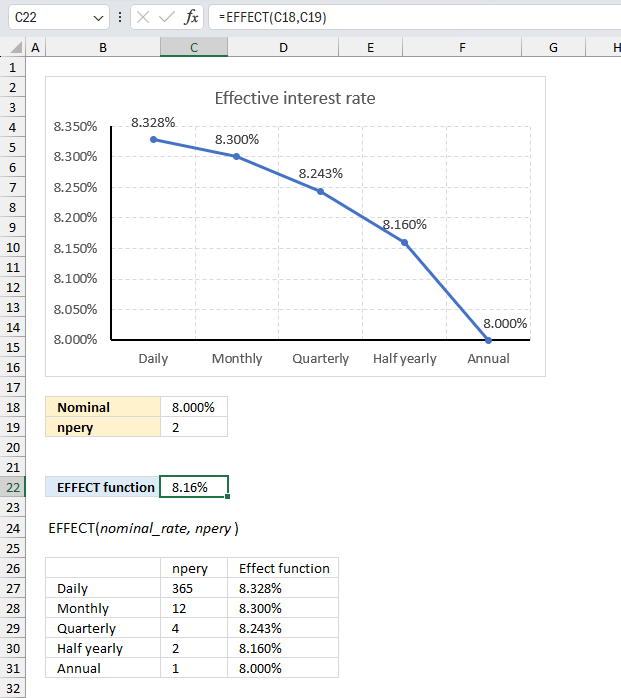
Formula in cell C22:
The formula in cell C22 returns 8.16% which represents the effective annual interest rate based of 8% compounded semi-annually.
The chart above shows the effective annual interest rate for different compounding periods, they are daily, monthly, quarterly, half yearly, and yearly. For an annual interest rate of 8% the effective interest rate for:
- daily compounding is 8.328%
- monthly compounding is 8.300%
- quarterly compounding is 8.243%
- half yearly is 8.160%
- annual is 8.000%
The EFFECT function calculates the effective annual interest rate using the following formula:
Effective Annual Rate = (1 + nominal_rate/npery)^npery - 1
(1 + 0.08/8)^2 - 1 is approximately 0.0816 or 8.160% This value matches the calculated value in cell C22.
5. Example 3
A bond pays a stated annual coupon rate of 6.2%, with interest compounded monthly. Determine the effective annual yield for this bond?
Arguments:
- nominal_rate: This is the nominal annual interest rate. Use a decimal value, not a percentage.
- npery: This is the number of compounding periods per year. This must be a positive integer.
An annual interest rate of 6.2% compounded monthly, the nominal_rate would be 0.062 (6.2% expressed as a decimal), and the npery would be 12 (12 months in a year).
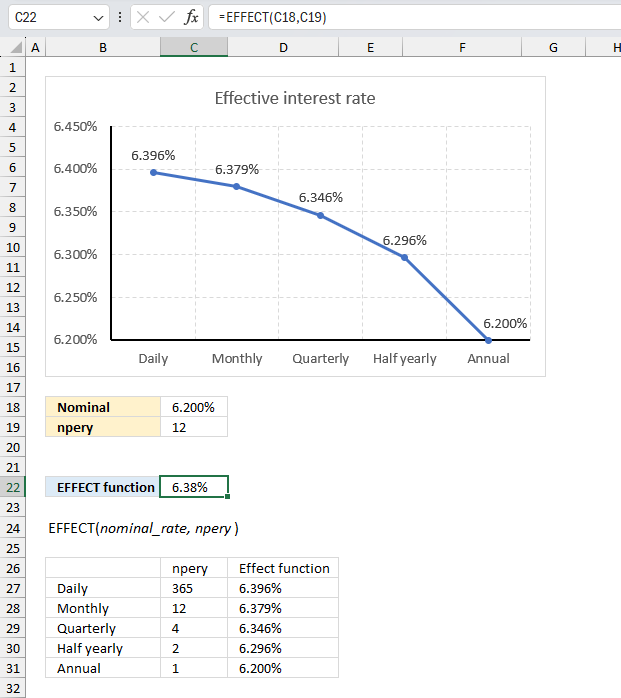
Formula in cell C22:
The formula in cell C22 returns 6.38% which represents the effective annual interest rate based of 6.2% compounded semi-annually.
The chart above shows the effective annual interest rate for different compounding periods, they are daily, monthly, quarterly, half yearly, and yearly. For an annual interest rate of 6.2% the effective interest rate for:
- daily compounding is 6.396%
- monthly compounding is 6.379%
- quarterly compounding is 6.346%
- half yearly is 6.296%
- annual is 6.2%
The EFFECT function calculates the effective annual interest rate using the following formula:
Effective Annual Rate = (1 + nominal_rate/npery)^npery - 1
(1 + 0.062/12)^12 - 1 is approximately 0.06379 or 6.379% This value matches the calculated value in cell C22.
Functions in 'Financial' category
The EFFECT function function is one of 27 functions in the 'Financial' category.
How to comment
How to add a formula to your comment
<code>Insert your formula here.</code>
Convert less than and larger than signs
Use html character entities instead of less than and larger than signs.
< becomes < and > becomes >
How to add VBA code to your comment
[vb 1="vbnet" language=","]
Put your VBA code here.
[/vb]
How to add a picture to your comment:
Upload picture to postimage.org or imgur
Paste image link to your comment.
Contact Oscar
You can contact me through this contact form