Excel solver examples
This article demonstrates solver in Excel.
Table of Contents
1. Introduction
What is the Excel Solver?
Excel Solver is a built-in optimization tool in Microsoft Excel that allows users to find optimal solutions for complex mathematical problems. It is used to find the values of decision variables that maximize or minimize an objective function while satisfying a set of constraints.
- Objective function: Solver can optimize a target cell (the objective function) by changing the values of other cells (the decision variables).
- Constraints: Solver can apply various constraints to the decision variables, such as upper and lower bounds, equality or inequality constraints, and integer or binary restrictions.
- Solver methods: Solver uses different optimization algorithms, such as the Generalized Reduced Gradient (GRG) method, the Simplex LP method, and the Evolutionary method, to find the optimal solution.
- Sensitivity analysis: Solver can perform sensitivity analysis to understand how changes in the input variables affect the optimal solution.
The Excel Solver add-in is a more basic free optimization tool built into Excel, while the standalone Solver software offers more advanced features and capabilities but at an additional cost. The choice between the two depends on the complexity of the optimization problem and the specific requirements of the user.
When to use the Excel Solver tool?
Excel Solver is commonly used in various applications such as:
- Resource allocation and scheduling
- Financial modeling and portfolio optimization
- Production planning and inventory management
- Engineering design and optimization
- Logistics and transportation problems
By using Excel Solver, users can find the best possible solution to their optimization problems, which can lead to improved decision-making, cost savings, and overall efficiency.
How to enable Solver in Excel 365?
Follow these steps to enable the Solver in Excel 365:
- Open the Excel Options menu by going to File > Options.
- In the Options window navigate to the Add-Ins tab.
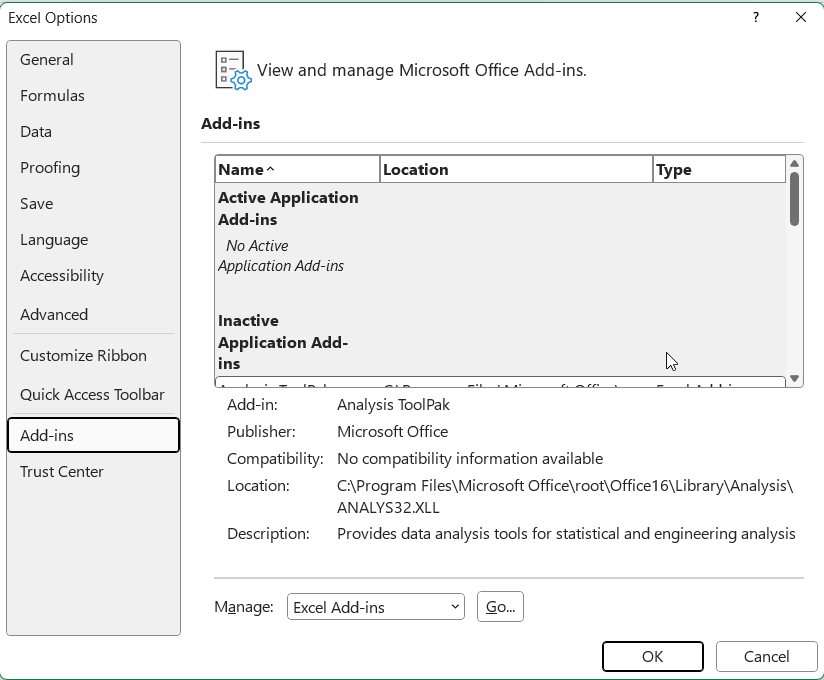
- In the Manage drop-down select "Excel Add-ins" and press with left mouse button on the "Go" button.
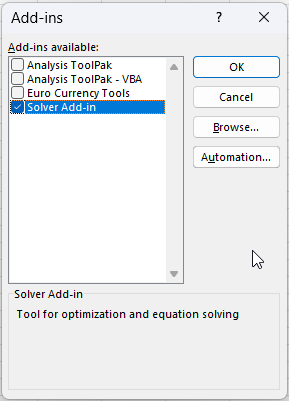
- In the Add-Ins available box, check the box next to the "Solver Add-in" and press with left mouse button on "OK".
After loading the Solver Add-in, the Solver command will be available in the Analysis group on the Data tab.

The image above shows the Solver button located on the "Data" tab on the ribbon.
- If the "Add-Ins available box" doesn't contain the Solver Add-in press with left mouse button on the "Browse" button to locate and select the add-in.
- If you get a message that the Solver Add-in is not currently installed then press with left mouse button on "Yes" to install it.
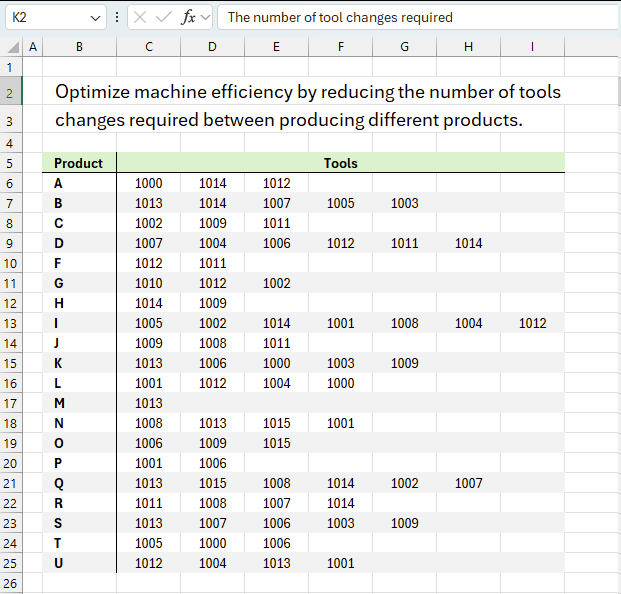
2. Optimize machine efficiency by reducing the number of tools changes required between producing different products

A given machine can produce 20 different products, each requiring different tools. Tool changes take time and reduce efficiency. The products, labeled A to U are listed in cells B6:B25. The range C6:I25 shows the tools needed for each product, they are numbered from 1000 to 1015. Some products need many tools, while others need only one. For example, product P requires two tools and they are: 1001 and 1006.
Our goal is to arrange the products in the best possible order to minimize the number of tool changes.
This is a classical traveling salesman problem (TSP). The issue here is that it takes too much time to compute because it is a combinatorial optimization problem with factorial complexity. Specifically, the number of possible solutions grows exponentially as more products are added.
Why does it take too much time?
TSP is classified as an NP-hard problem, meaning no known algorithm can solve it efficiently for large inputs. Thus, solving the TSP exactly for 20 products is infeasible with brute-force methods due to the astronomical number of route combinations. Excel Solver likely finds a near-optimal solution using heuristics and optimization techniques rather than brute-force enumeration. Excel Solver typically uses the GRG Nonlinear or Evolutionary Solver algorithm which are not designed for exact solutions to NP-hard problems but rather for finding good approximations within a reasonable time.
Let’s use the "Solver" to find an optimized solution. First we need to calculate the number of tool changes between all products.
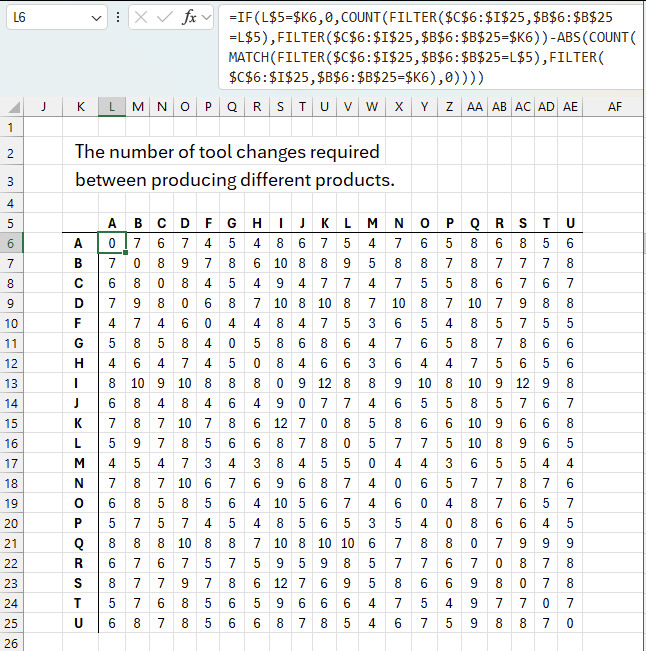
The table above shows products both horizontally and vertically in L5:AE5 and in cells K6:K25. The numbers in L6:AE25 represents the number of tool changes between two products. For example:
- Find product "A" in L5:AE5 and also product "A" in K6:K25, the intersecting cell is L6 which contains 0 (zero). This means that zero tool changes are required between product "A" and product "A" which makes sense because they require the same tools.
- Find product "I" and "K", the intersecting cell is S15 which contains 12. This means that changing from product "I" to product "K" requires 12 tools to be changed.
Product "I" needs 7 tools: 1005, 1002, 1014, 1001, 1008, 1004, and 1012. All 7 tools needs to be uninstalled.
Product "K "requires 5 tools: 1013, 1006, 1000, 1003, and 1009. All 5 tools need to be installed. Products "I" and "K" share no tools what so ever.
The formula for calculating how many tools to change is:
Basically, the formula filters the tool numbers based on product and counts the difference. The table is needed for solver to find the optimal manufacturing configuration.
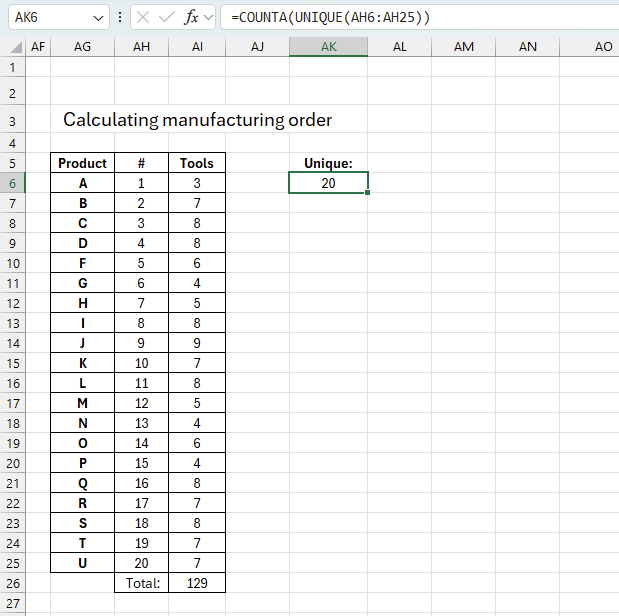
The image above shows the products that need to be manufactured in cells AG6:AG25. The corresponding cells in column AH show the number of times tools needed to be changed. Cell AH26 shows the total number of times. For example, tool "A" (cell AG6) has 3 tools to be installed, changing from "A" to tool "B" (cell AG7) involves uninstalling 3 tools and installing 4 tools, in total 7 tools displayed in cell AH7.
Formula in cell AI6:
This formula counts the number of tools for the first product in cell AH6. Formula in cell AH7:
Copy cell AH7 and paste to cells below as far as needed. This formula counts the number of tools to be uninstalled and installed excluding shared tools. Formula in cell AK6:
=COUNTA(UNIQUE(AH6:AH25))
We need the formula in cell AK6 to make sure Solver doesn't use duplicates in AH6:AH25. Formula in cell AI26:
Cell AI26 adds all the tools and returns a total. The total is recalculated each time solver changes the order, this makes it possible to find a minimum value.
You may now have realized that this problem is the "Traveling salesman" problem or TSP. The Traveling Salesman Problem (TSP) is a classic optimization problem in mathematics. The goal is to find the shortest possible route for a "salesman" to visit a given set of destinations exactly once and return to the starting city. Each city is connected by a route with a specific distance, and the objective is to minimize the total cost of the trip. TSP is an NP-hard problem meaning there is no known algorithm that can solve it efficiently for all instances. As the number of cities increases the computation time required to find the exact solution grows exponentially.
The number of possible routes grows rapidly with the number of destinations. For n cities, there are (n−1)! possible routes to evaluate since the starting city is fixed.
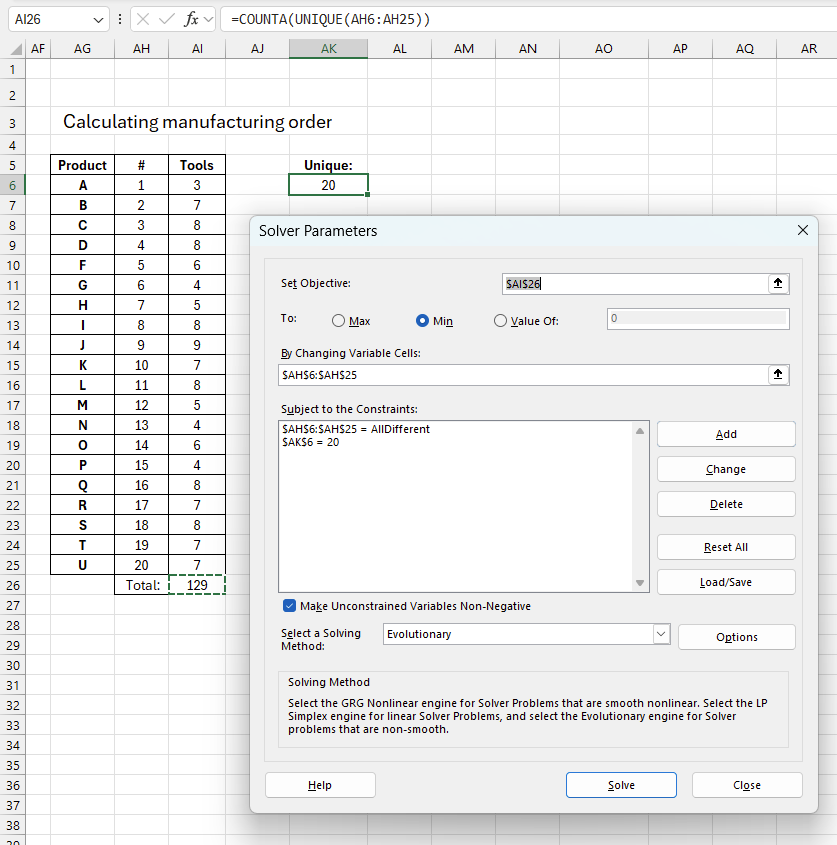
Go to tab "Data", press with left mouse button on the "Solver" button to start Solver. A dialog box appears, see the image above.
3. Using Excel Solver to schedule employees
This is a question I found at the bottom of this page Using Solver to schedule your workforce (Microsoft has now removed this question from their website)
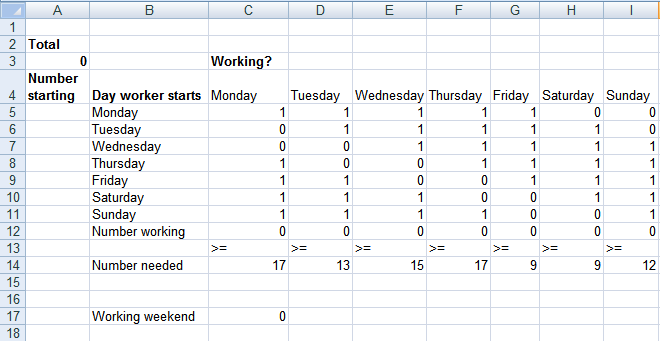
"Bank 24" processes checks 7 days a week. The number of workers needed each day to process checks is 17 workers are needed on Monday, 13 workers are needed on Tuesday, 15 workers are needed on Wednesday, 17 workers are needed on Thursday, 9 workers are needed on Friday, 9 workers are needed on Saturday and 12 workers are needed on Sunday. All bank employees work five consecutive days.
Suppose our bank had 22 employees, and that their goal was to schedule employees so that they would have the maximum number of weekend days off. How should the workers be scheduled?
Here is the setup:
Here is a break-down of the image above:
Cell range A5:A11: This column represents the "Number starting" for each day of the week. It shows how many workers start their shift on each day:
- Monday: 5 workers
- Tuesday: 5 workers
- Wednesday: 0 workers
- Thursday: 0 workers
- Friday: 0 workers
- Saturday: 4 workers
- Sunday: 8 workers
Cell range C5:I11: This is a data table showing the working schedule for each day. A "1" indicates that a worker who started on that row's day is working on that column's day. For example:
- Workers starting on Monday (row 5) work Monday through Friday.
- Workers starting on Tuesday (row 6) work Tuesday through Saturday.
- This pattern continues, with each worker having a 5-day work week.
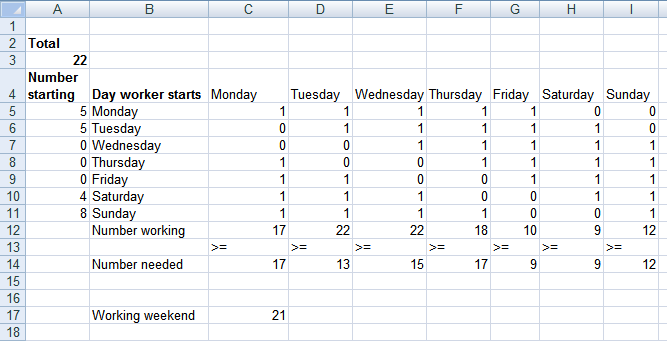
Objective: To minimize the value in cell $C$17,
By changing variable cells: $A$5:$A$11 (the number of workers starting each day)
Subject to the constraints:
- $A$3 = 22 (total number of workers)
- $A$5:$A$11 = integer (ensuring whole numbers of workers)
- $C$12:$I$12 >= $C$14:$I$14 (ensuring the number of workers each day meets or exceeds the needed number)
I created a new formula in C17. This formula adds the number of workers working on a saturday and on a sunday, it returns a total that the Solver can use to minimize the number of workers working on the weekend.
All other formulas are created in the initial setup, see xls file found here: Using Solver to schedule your workforce (The .xls file is removed from the Microsoft webpage)
3.1 How to schedule employees so that they would have the maximum number of weekend days off
- Press with left mouse button on Data on the Ribbon
- Press with left mouse button on Solver
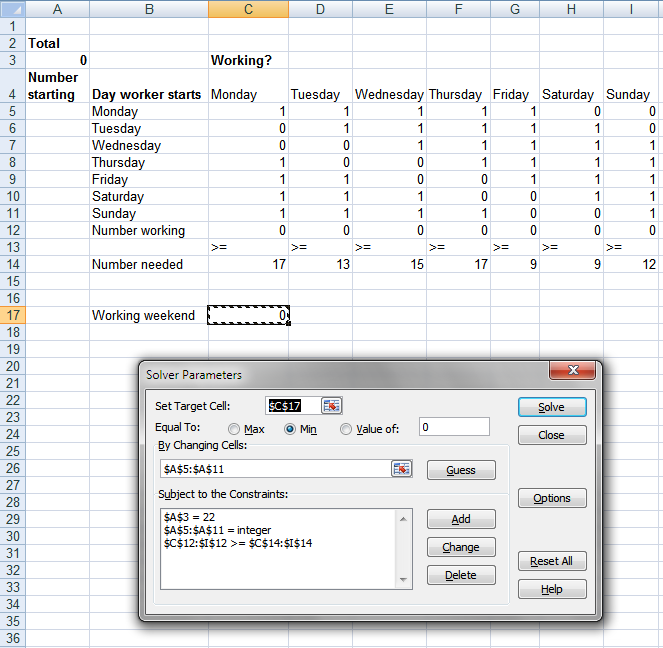
- Press with left mouse button on "Start Target Cell" button and select C17
- Press with left mouse button on Min in "Equal To:"
- Press with left mouse button on "By Changing Cells:" button and select A5:A11
- Press with left mouse button on Add button
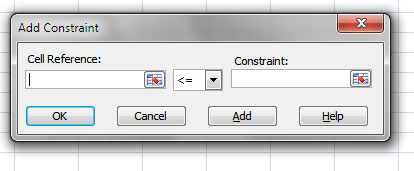
- Press with left mouse button on "Cell Reference:" button and select A3
- Press with left mouse button on triangle and select "="
- Type 22 in "Constraint:" window
- Press with left mouse button on Add
- Press with left mouse button on "Cell Reference:" button and select A5:A11
- Press with left mouse button on triangle and select "integer"
- Press with left mouse button on Add
- Press with left mouse button on "Cell Reference:" button and select C12:I12
- Press with left mouse button on triangle and select ">="
- Press with left mouse button on "Constraint:" button and select C14:I14
- Press with left mouse button on OK!
- Press with left mouse button on Solve.
The Solver uses these parameters to adjust the number of workers starting each day (A5:A11) to find the optimal schedule that minimizes the objective while meeting all constraints. It does this using the Simplex LP (Linear Programming) method, which is appropriate for this type of linear optimization problem.
The Solver iteratively tries different combinations of starting workers each day, checking if the constraints are met and evaluating the objective function. It continues this process until it finds the optimal solution that minimizes the objective while satisfying all constraints.
This approach allows for efficient scheduling of workers to meet daily needs while minimizing some cost or inefficiency metric.
Get excel sample file for this article.
bank24_1.xls
(Excel 97-2003 Workbook *.xls)
4. Cash drawer bill extractor
Question:
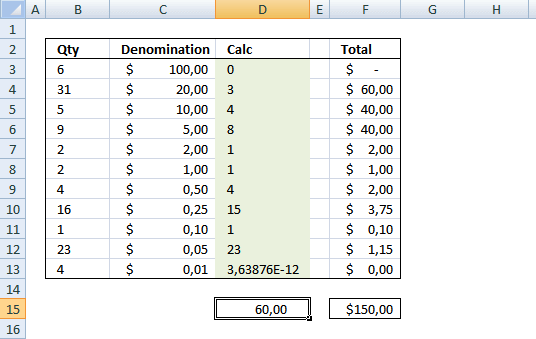
I need to setup a template to remove the largest available (Qty and denomination)bills and leave exactly $150 back in the cash drawer in small bills, change and rolls of change. I need to remove exactly $ 1178.29 in large bills and leave the remaining $150 (from a total of $1328.29 in the register) in small bills and change.
Answer:
I am using excel solver to find a solution. Here is how to install the Solver add-in in Excel.
- Press with left mouse button on Office button
- Press with left mouse button on Excel Options
- Press with left mouse button on add-ins
- Install Solver
- Press with left mouse button on OK
How to use this template
- Select max quantities in cell range B3:B13
- Start excel solver, it is on tab "Data" on he ribbon.
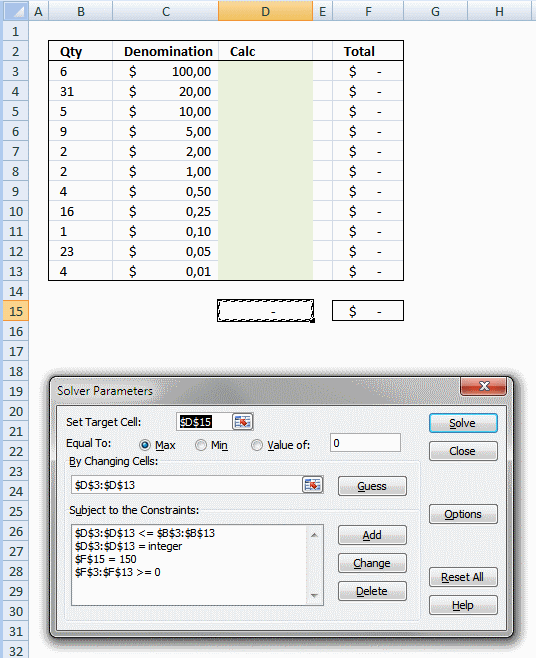
Change constraint in excel solver
- Press with left mouse button on $F$15 in "Subject to the constraints:" window
- Press with left mouse button on Change button
- Change value to your specific sum
- Press with left mouse button on OK
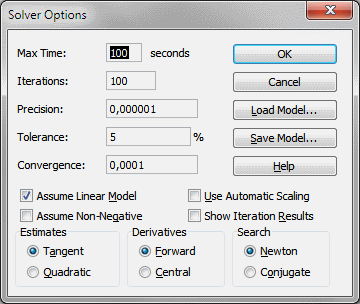
Press with left mouse button on options button and enable "Assume Linear Model".
Press with left mouse button on OK.
Press with left mouse button on Solve button
Solver category
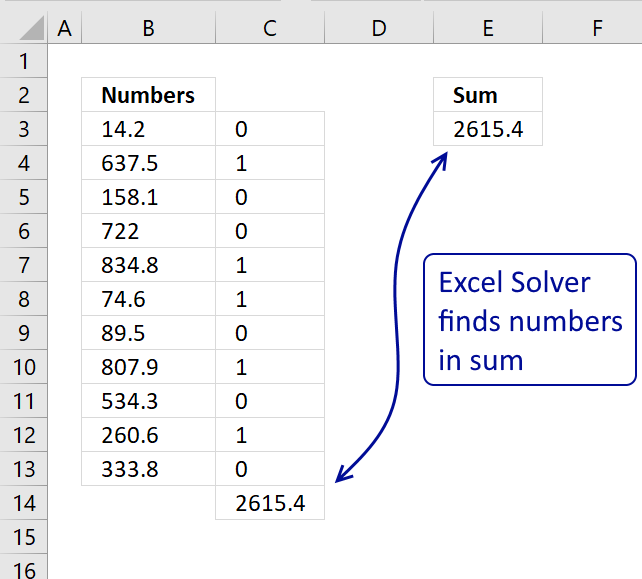
Table of Contents Identify numbers in sum using Excel solver Find numbers in sum - UDF Find positive and […]
The COMBIN function returns the number of combinations for a specific number of elements out of a larger number of […]
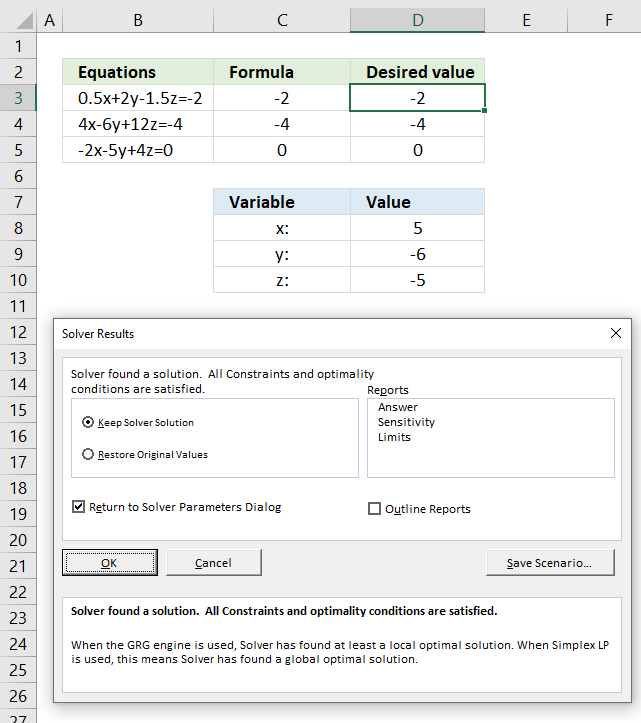
This article demonstrates how to solve simultaneous linear equations using formulas and Solver. The variables have the same value in […]
Excel categories
One Response to “Excel solver examples”
Leave a Reply
How to comment
How to add a formula to your comment
<code>Insert your formula here.</code>
Convert less than and larger than signs
Use html character entities instead of less than and larger than signs.
< becomes < and > becomes >
How to add VBA code to your comment
[vb 1="vbnet" language=","]
Put your VBA code here.
[/vb]
How to add a picture to your comment:
Upload picture to postimage.org or imgur
Paste image link to your comment.

I believe there is a typo in the blog, particularly in the first example it the formula =INDEX($L$6:$AE$25, MATCH(AG6, $L$5:$AE$5, 0), MATCH(AG7, $K$6:$K$25, 0))
should be applied on AI7 rather than AH7. Kindly verify this and update the blog accordingly, so the other don't get stuck here.
Regards